预测的流程和方法（Forecasting: Principles and practice第三章）

3. the forecaster’s toolbox
   3.1 a tidy forecasting workflow
   生成时间序列数据预测可分为以下几步：
   

数据准备（整理）
数据的准备方式还可以用于探索时间序列的不同特征；预处理数据集是使用交叉验证评估模型性能的重要步骤。

绘制数据（可视化）

定义模型（指定）
在将模型拟合到数据之前，我们首先必须描述模型。 有许多不同的时间序列模型可用于预测，为数据指定适当的模型对于产生适当的预测至关重要。

训练模型（估计）
对于线性变量中每个关键变量的组合，这将线性趋势模型拟合到GDP数据。 在此示例中，它将使模型适合数据集中的263个国家/地区。 生成的对象是模型表或“ mable”。

检查模型性能（评估）
拟合模型后，重要的是检查模型对数据的性能。 有几种诊断工具可用于检查模型行为，还有一些准确性度量，可以将一个模型与另一个模型进行比较。

产生预测（预测）

3.2 some simple forecasting methods
Average method
所有未来值的预测等于历史数据的平均值（或“平均值”）。

Naïve method（随机游走预测）
对于Naive预测，我们仅将所有预测设置为最后一次观察的值。

对于许多经济和金融时间序列，此方法都非常有效。
随机游走预测（Naïve method）: 将所有预测设置为最后一次观察的值， 因为当数据遵循随机游走时Naive的预测是最佳的（请参见第9.1节）

Seasonal naïve method
对于高度季节性的数据，类似的方法也很有用。 在这种情况下，我们将每个预测设置等于一年中同一季节（例如，去年的同一个月）的最后观察值。 正式地，对时间的预测

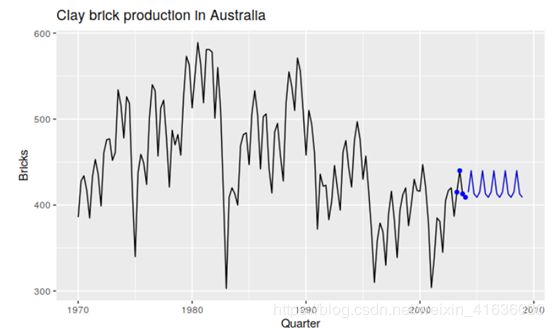
Drift method
对于naïve method一种变化的方式是允许预测随着时间而增加或者减少，这种随着时间而变化量的幅度可以设置为历史数据中的平均变化



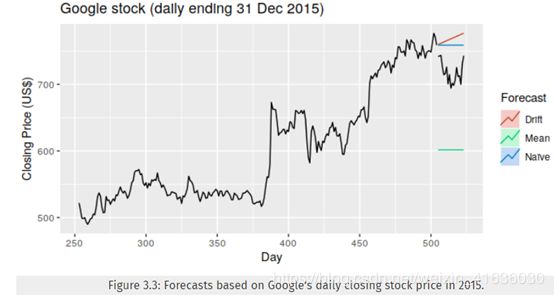
有时，这些简单方法之一将是可用的最佳预测方法。 但在许多情况下，这些方法将作为基准，而不是选择的方法。 也就是说，我们开发的任何预测方法都将与这些简单方法进行比较，以确保新方法比这些简单方法更好。 如果不是这样，那么新方法就不值得考虑。该方法已应用到Google在2015年的每日收盘价中，并用于预测未来一个月的价格。 由于不是每天都观察到股票价格，因此我们首先根据交易日而不是日历日建立新的时间指数。

3.3 transformation and adjustments
4种调整历史数据方式：
1） 日历调整
2） 人口调整
3） 通货膨胀调整
4） 数据转换
目的是通过删除已知的异常点或通过使模式在整个数据集中保持一致性来简化历史数据中的模式，因为简单的模式能够导致更加准确的预测

日历调整
季节性数据中出现的某些变化可能是由于简单的日历影响，故在拟合预测模型前先删除差异。
Ex：在研究零售商店的月度总销售额，则月度间会有差异，这是由于除了全年季节性变化外，每月交易日数也不同。通过计算每月交易日的平均销售额而不是该月的总销售额，可轻松消除这种差异，从而有效删除了日历变化。

人口调整
任何受人口变化影响的数据都可进行调整以提供人均数据，即考虑每人的数据而不是总数。
Ex：在研究特定地区随时间推移的病床数量，则考虑每千人的病床数量来消除人口变化的影响，就更加容易解释。对于大多数受人口变化影响的数据，最好使用人均数据而不是总数。

通货膨胀调整
受货币价值影响的数据最好在建模前进行调整
Ex：由于通货膨胀，新房子平均成本在过去几十年中增加；因此，通过调整财务时间序列，以使所有值都以特定年份的美元值表示

数学变换
如果数据显示随系列水平增加或减少的变化，则转换可能会有用。
Ex：对数的变换很有用，如果原始的观测值为 。
，那么转换后的观测值为 。
对数的有效在于它的可解释性。对数值得变化是原始比例相对（或百分比）变化；故若用对数基数10，则对数标度上的增加1对应于原始标度上的10的乘积。对数转换另一个有用功能是它们将预测约束为在原始范围内保持正数。
有时其他的转换也有用，比如平方根或者立方根，它们被称作幂变换因为它们被写成

Box-Cox变换包含了幂变换和对数变换，且它依赖于参数lambda，能够被定义为：

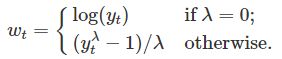
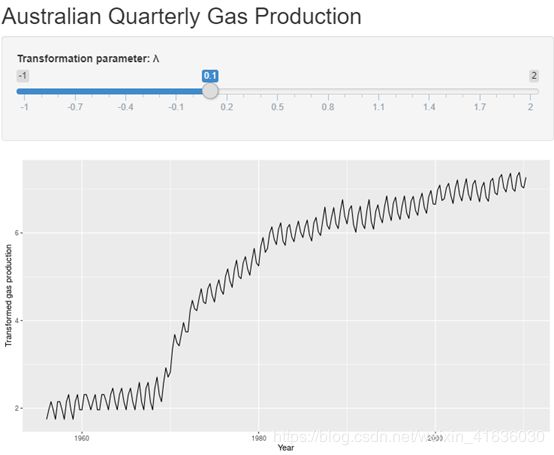
一个好的λ是使整个系列的季节性变化量大致相同的一种方法，因为这样可以简化预测模型。 在这种情况下，λ=0.10效果很好，尽管λ 在0到0.2之间会得到相似的结果。

在前面选择转换后，我们需要预测转换后的数据。 然后，我们需要逆向转换（或back-transform）以获得原始比例的预测。 Box-Cox逆变换由下式给出:

幂转换的特征
 如果有些yt≤0，则不能用幂转换，除非所有的值都被增加了一个常数使其为正数
 选择一个简单的λ，使它解释更容易
 λ对于预测结果相对不敏感
 通常不需要进行任何转换
 转换有时对预测影响不大，但对预测间隔影响很大。

转换组合
转换的组合扩展了可以实质性修改因变量的方式。 Box-Cox转换（λ≠0）可以分解为几个更简单的转换（乘法，加法和幂运算）。
Ex：对数转换可确保所得的预测将是非负的，这对于约束合理数据尤其有吸引力。
但是，对数转换不能用于0（或负）观测值的数据；相反，log(x+1)可以用在包含0的数据的对数转换上，转换的大多数组合都可以用这种方式表示。

另一个有用的转换时缩放的logit，可用于确保将预测保持在特定时间间隔内。一个缩放的logit可确保预测值在a和b范围内（a
反转此转换可进行适当反向转换：

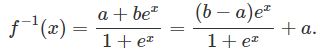
通过定义此新的转换函数，现在可以将预测限制在指定的间隔内。 例如，要将预测限制在0到100之间，可以使用scaled_logit（y，0，100）作为模型的左侧公式。

偏差调整
使用数学变换（box-cox变换）的问题：逆变换的点预测不是预测分布的均值，通常是预测分布的中位数。
对于许多预测来说，这是可接受的，但有时需要用平均预测，比如希望汇总各个地区销售预测以形成整个国家的预测，但中位数不会加起来，而平均值可以。
对于Box-Cox变换，反变换后的均值由下式给出：

这里的 是转换后的h步的预测方差，预测方差越大，均值和中位数间的差异越大。

前面的简单逆变换预测与平均值逆变换的预测间的差异称为偏差；当我们使用平均值而不是中位数时，我们说点预测已经进行了偏差调整。

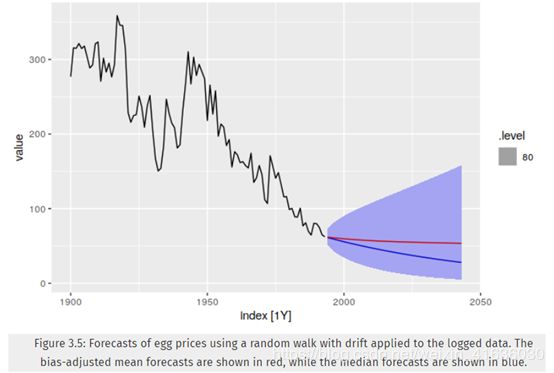
图3.5中的蓝线显示了预测中位数，红线显示了预测均值。 请注意，当我们使用偏差调整时，偏斜的预测分布如何拉高点预测。

3.5 fitted values and residuals
拟合值：使用所有之前的观测值来预测时间序列的每个值，我们称这些值为拟合值，且它们被标记为 ，意思是预测值yt是基于观测值 ，通常拟合值始终涉及单步预测。

残差
时间序列模型中的残差是拟合模型后剩下的残差；对于大多数时间序列模型，残差等于观测值与相应拟合值之间的差。

残差在检查模型是否已充分捕获数据中的信息时很有用。 如果在残差中可以观察到模式，则可以改进模型。

3.5 prediction intervals
预测间隔给出了我们期望Yt会以指定的概率落到一定的间隔范围内。
例如，假设残差是正态分布的，则对于h步的95%的预测间隔为：

是h步的预测分布标准差；更广泛地，我们可以称为
而这里的乘子c取决于覆盖率。

预测间隔的值是它们表示预测中不确定性；如果仅生成点预测，则无法说明预测的准确性，但如果还生成预测间隔，那么可以知道每个预测有多少不确定性。因此，没有附带预测间隔，点预测几乎没有价值。

一步预测间隔
在向前一步预测时，预测分布标准偏差与残差的标准偏差几乎相同。
Ex: 考虑对Google股票价格数据google_2015的naive预测（如图3.3所示）。 观测序列的最后一个值是758.88，因此对GSP下一个值的预测是758.88。 朴素方法的残差标准偏差为11.19。 因此，下一个GSP值的95％预测间隔为

多步预测间隔
预测间隔的一个共同特征是它们的长度随着预测范围的增加而增加。 我们预测的越远，预测的不确定性就越大，因此预测间隔越宽。
换句话说，σh通常随着h增加（尽管有些非线性预测方法不具有此属性）。

为了产生预测间隔，有必要估算σh；对于单步预测（h=1），则残留的标准偏差可很好估算预测标准偏差；对于多步预测，则需更复杂的方法，这些计算假定残差是不相关的。

基准方法
对于以下四种基准方法，可以在残差不相关的假设下以数学方式得出预测标准偏差。

Bootstrapped残差的预测间隔
当残差的正态分布是不合理的假设时，一种替代方法是使用自举法，该方法仅假设残差不相关。
一步预测误差定义为： ；我们可写为 ；那么可模拟它的下一步时间序列观察值为： ，这里的 是一步预测值，而 是未知的未来错误。假设未来的error类似于过去的errors,那么我们能够通过在过去的错误集合（即残差）中采样，将新的模拟观测值添加到我们的数据集中，我们可以重复该过程得到
反复这样做，我们可以获得许多可能的未来。 然后，我们可以通过计算每个预测范围的百分位数来计算预测间隔。 结果称为自举预测间隔。 “引导程序”这个名称是指通过引导程序来提高自己的能力，因为该过程允许我们仅使用历史数据来衡量未来的不确定性。

预测间隔与变换
如果已使用转换，则应在转换后的比例上计算预测间隔，并对端点进行反转换以在原始比例上给出预测间隔。 这种方法保留了预测间隔的概率覆盖范围，尽管它不再围绕点预测对称。