GDBT 通过《统计学方法例题》推导深刻理解算法原理。
GBDT 原理
看完你保证明白
公式编写起来太费时间,这里我就贴图吧(图片来源)

回归问题的提升树算法可以看周志华老师的《统计学习放法》,里面例题讲解特别详细。
我们主要根据提升树例题讲解GBDT
好了我们开始上例题进行讲解:
- 看过统计学习方法的同学应该不陌生吧。
- 那么下面让我们用GBDT来进行解题。
1.我们初始化一个弱学习器
f 0 ( x ) = a r g m i n c ∑ i = 1 N L ( y i , c ) f_0(x) = arg min_c ∑_{i=1}^N L(y_i,c) f0(x)=argminc∑i=1NL(yi,c)
对这个弱学习器进行求导。
我们定义损失函数: L ( y i , f ( x i ) = 1 / 2 ( y i − f ( x i ) ) 2 L(y_i,f(x_i) = 1/2(y_i-f(x_i))^2 L(yi,f(xi)=1/2(yi−f(xi))2
那么求导后

标签 y = [5.56, 5.70, 5.91, 6.4, 6.8, 7.05, 8.9, 8.7, 9, 9.05]
c = 标签 y 的平均值 = 7.307
,
得到初始学习器 f 0 ( x ) = c f_0(x) = c f0(x)=c = 7.307
得到初始学习器,我们就可以为下一个学习器算出需要用来拟合的残差。
2.求残差 r r r
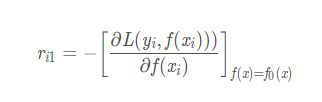
得到 y − f 0 ( x ) = r 11 y-f_0(x) = r_{11} y−f0(x)=r11
x = [ 1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
y = [-1.747 -1.607 -1.397 -0.907 -0.507 -0.257 1.593 1.393 1.693 1.743]
这是 r i 1 r_{i1} ri1 代替了标签 y i y_i yi 作为下一个弱学习的输入标签。
第一个弱学习器,就是瞎子都能看出来是垃圾,所以我们根本就没必要计算损失值。为此我们进行创造第二个弱学习器。
. 用不同切分点遍历数据集,找出最小平方差。与最小平方差对应的切分点就是最佳切分点
我用代码算出 5.5 是最好的切分点 并找出了 R 11 R_{11} R11 和 R 22 R_{22} R22 切分后各自的 c 1 = 1.858133 c1 =1.858133 c1=1.858133、 c 2 = 0.071875 c2 = 0.071875 c2=0.071875 值.。
2. 这时我们就创建了第二弱学习器
h 1 ( x ) = ∣ c 2 − − − x > 5.5 c 1 − − − x < 5.5 h_1(x) = |_{c2---x>5.5}^{c1---x<5.5} h1(x)=∣c2−−−x>5.5c1−−−x<5.5
把第一个弱学习和第二学习组合就成了一个最初雏形的强学习器了
f 1 ( x ) = f 0 ( x ) + h 1 ( x ) f_1(x) = f_0(x) + h_1(x) f1(x)=f0(x)+h1(x)
我们这时可以试着算算损失值是否达到我们想要的
L ( y i , f 1 ( x ) ) = 1 / 2 ( y i − ( f 0 ( x ) + h 1 ( x ) ) ) 2 L(y_i,f_1(x)) = 1/2(y_i - (f_0(x)+h_1(x)))^2 L(yi,f1(x))=1/2(yi−(f0(x)+h1(x)))2 = 0.965
垃圾,我们还要继续…
原谅我不会敲公式 - - 好烦。
既然有了第二弱学习器,我们就可以为第三个弱学习器算出需要用来拟合的残差。
损失函数求负偏导: − L ( y i , f 1 ( x ) ) = 1 / 2 ( y i − ( f 0 ( x ) + h 1 ( x ) ) ) 2 -L(y_i,f_1(x)) = 1/2(y_i - (f_0(x)+h_1(x)))^2 −L(yi,f1(x))=1/2(yi−(f0(x)+h1(x)))2
得出偏导数: y − f 0 ( x ) − h 1 ( x ) y-f_0(x)-h_1(x) y−f0(x)−h1(x)
根据公式: r i 1 = y i − f m − 1 ( x ) r_{i1} = y_i - f_{m-1}(x) ri1=yi−fm−1(x)
最终偏导数: r 11 − h 1 ( x ) r_{11} - h_1(x) r11−h1(x)
更新残差
即 r 11 − h 1 ( x ) = r 21 r_{11} - h_1(x) = r_{21} r11−h1(x)=r21
r_21 = [-0.67666667,-0.53666667,-0.32666667,0.16333333,0.56333333,0.81333333,-0.0125,-0.2125,0.0875,0.1375]
. 继续用不同切分点遍历数据集,找出最小平方差。与最小平方差对应的切分点就是最佳切分点
我用代码算出 2.5 是最好的切分点 并找出了 R 11 R_{11} R11 和 R 22 R_{22} R22 切分后各自的 c 1 = 0.062067 c1 =0.062067 c1=0.062067、 c 2 = 0.738608 c2 = 0.738608 c2=0.738608 值.。
到这里我们知道第三个弱学习器
h 2 ( x ) = ∣ c 2 − − − x > 2.5 c 1 − − − x < 2.5 h_2(x) = |_{c2---x>2.5}^{c1---x<2.5} h2(x)=∣c2−−−x>2.5c1−−−x<2.5
把第一个弱学习、第二个弱学习、第三个组合就成了一个强学习器
f 2 ( x ) = f 0 ( x ) + h 1 ( x ) + h 2 ( x ) = f 1 ( x ) + h 2 ( x ) f_2(x) = f_0(x) + h_1(x)+h_2(x) = f_1(x) + h_2(x) f2(x)=f0(x)+h1(x)+h2(x)=f1(x)+h2(x)
我们这时可以试着算算损失值是否达到我们想要的
L ( y i , f 2 ( x ) ) = 1 / 2 ( y i − ( f 1 ( x ) + h 2 ( x ) ) ) 2 L(y_i,f_2(x)) = 1/2(y_i -( f_1(x)+h_2(x)))^2 L(yi,f2(x))=1/2(yi−(f1(x)+h2(x)))2 = 0.4003
哎呦不错哦
既然有了第三弱学习器,我们就可以为第4个个弱学习器算出需要用来拟合的残差。
损失函数求负偏导: − L ( y i , f 2 ( x ) ) = 1 / 2 ( y i − f 1 ( x ) − h 2 ( x ) ) 2 -L(y_i,f_2(x)) = 1/2(y_i - f_1(x)-h_2(x))^2 −L(yi,f2(x))=1/2(yi−f1(x)−h2(x))2
得出偏导数: r 21 − h 2 ( x ) r_{21} - h_2(x) r21−h2(x)
更新残差
即 r 21 − h 2 ( x ) = r 31 r_{21} - h_2(x) = r_{31} r21−h2(x)=r31
r_31 = [-0.16333333 -0.02333333 0.18666667 -0.05666667 0.34333333 0.59333333 -0.2325 -0.4325 -0.1325 -0.0825]
继续用不同切分点遍历数据集,找出最小平方差。与最小平方差对应的切分点就是最佳切分点
我用代码算出 5.5 是最好的切分点 并找出了 R 11 和 R 22 R_{11}和R_{22} R11和R22
切分后各自的 c 1 = 0.406133 c1 =0.406133 c1=0.406133、 c 2 = 0.0.071875 c2=0.0.071875 c2=0.0.071875值.。
‘’’’’’’’’’’'构造了第4个弱学习器。组合成强学习器后,我们计算损失值=0.23
哎呦不错诶,还能往下继续的,不过到这里,大家差不多已经明白GBDT的运算规则了。



