Leetcode一起攻克动态规划

leetcode上动态规划方向的题目大多是medium，而且题目解答也很难理解，所以我打算写一篇博客，来给大家一些建议，包括刷dp的顺序，以及超级详细的解答。

题目链接

1.石子游戏：属于入门级别的题目，第一次刷可能有难度，不会的话建议看下答案。
2.最小路径和很好的入门题目。
3.三角形最小路径和：很好的去理解什么是动态规划。
4.下降路径最小和：三角形最小路径和加强版，建议刷完第3题去刷第四题。
5.不同路径：刷到这里的时候就应该有一定水平了，强烈建议这道题一定不要看答案，要自己a出来。
6.不同路径二：刷完第五题，可以跟着去刷这道题，相对来说算法只是有些改动
7.整数拆分：经典的动态规划入门题目。
8.最长数对链：只能说还可以，因为贪心算法更合适，不过也可以用来理解动态规划。
9.买卖股票的最佳时机含手续费
10.计算各个位数不同的数字个数
11.使用最小花费爬楼梯：经典中的经典。
12.只有两个键的键盘：练习dp的经典题目。
13.预测赢家：与石子游戏几乎一模一样。
14.最长回文子序列个人认为14题更考察dp。
15.最长回文子串：14与15一定要连着做。能够比较好的去理解题目，15题的dp数组主要作用就是判断这一段是否可用。
16.组合总数IV很好的一道dp题。
17.最长重复子数组，这道题不同的是二维数组数组dp[i][j],表示的不是A数组从0到i-1，与B数组从0到j-1之间的最大重复子数组，而是代表以A[i-1]与B[j-1]结尾的公共字串的长度。
18.完全平方数
19.最低票价
20.零钱兑换这题最大的亮点就是不可以用贪心算法。
21.乘积最大子序列最大的亮点就是要注意负负得正。
22.最小路径和：很容易想出自底向上的解法
23.打家劫舍：理解什么是状态，什么是状态的转移。
24.打家劫舍 II更深入理解上一个题的通用思路
25.买卖股票的最佳时机
26.打家劫舍 III怎么感觉这个题更简单一点呢
27.编辑距离看着挺难其实不难
28.分割等和子集背包问题的最好练手题
29.一和零
30.单词拆分
31.目标和
32.零钱兑换 II
33.抛掷硬币
34.最长上升子序列
35.摆动序列
36.最长公共子序列

建议顺序

这个顺序是按照玩转Leetcode题库分门别类详细解析顺序与个人理解总结的。

1.理解记忆化搜索与动态规划

1.使用最小花费爬楼梯：经典中的经典。
2.三角形最小路径和：很好的去理解什么是动态规划。
3.最小路径和：很容易想出自底向上的解法
4.整数拆分：经典的动态规划入门题目。
5.完全平方数
6.不同路径：刷到这里的时候就应该有一定水平了，强烈建议这道题一定不要看答案，要自己a出来。
7.不同路径二：刷完上一道题题，可以跟着去刷这道题，相对来说算法只是有些改动

2.理解状态与状态的转移

1.打家劫舍：理解什么是状态，什么是状态的转移。
2.打家劫舍 II更深入理解上一个题的通用思路。
3.打家劫舍 III怎么感觉这个题更简单一点呢

3.背包问题

1.0-1背包问题

问题描述，有一个容量为C的背包，总共有N个物品，每个物品都有价值和其重量，如何在满足容量C的条件下，尽可能的获得最高价值。
定义转移方程 best（i,c）在前i个物品中在容量c的情况下尽可能获得最高价值：

  best(i,c) = max(v（i）+best(i-1,c-w(i)),best(i-1,c))
  将第i个加入背包，或不将第i个加入背包

普通递归

public class Main {
    
    private static int times = 0;
    
    public static void main(String[] args) {
        int[]values = new int[]{6,10,12,14};
        int[]weights = new int[]{1,2,3,4};
        int C = 5;
        System.out.println("最优结果为"+solve01package(values,weights,C));
        
    }
    public static int solve01package(int[]values,int[]weights,int C)
    {
         return best(values,weights,values.length-1,C); 
    }
    public static int best(int[]values,int[]weights,int i,int cap){
        times++;
        System.out.printf("循环次数为"+times+"当前考虑的为：best(%d,%d)",i,cap);
        System.out.println();
        if(i<0||cap<=0)
        return 0;
        int nochosei = best(values,weights,i-1,cap);
        int chosei = 0;
        if(cap>=weights[i])
        chosei = values[i]+best(values,weights,i-1,cap-weights[i]);
        int max = Math.max(chosei,nochosei);
        return max;
    }
}

记忆化搜索

核心就是加上了一个memo数组用来判断存放前i个物品，容量为c这个事我是否做过。

// "static void main" must be defined in a public class.
public class Main {
    /*
    问题描述，有一个容量为C的背包，总共有N个物品，每个物品都有价值和其重量，如何在满足容量C的条件下，尽可能的获得最高价值。
    定义转移方程 best（i,c）在前i个物品中在容量c的情况下尽可能获得最高价值：
    best(i,c) = max(v（i）+best(i-1,c-w(i)),best(i-1,c))
    将第i个加入背包，或不将第i个加入背包
    */
    private static int times = 0;
    private static int[][]memo;
    public static void main(String[] args) {
        int[]values = new int[]{6,10,12,14};
        int[]weights = new int[]{1,2,3,4};
        int N = values.length;
        int C = 5;
        memo = new int[N][C+1];
        for(int i=0;i<N;i++)
        {
            Arrays.fill(memo[i],-1);
        }
        System.out.println("最优结果为"+solve01package(values,weights,C));
        
    }
    public static int solve01package(int[]values,int[]weights,int C)
    {
         return best(values,weights,values.length-1,C); 
    }
    public static int best(int[]values,int[]weights,int i,int cap){
        times++;
        System.out.printf("循环次数为"+times+"当前考虑的为：best(%d,%d)",i,cap);
        System.out.println();
        if(i<0||cap<=0)
            return 0;
        if(memo[i][cap]!=-1)
            return memo[i][cap];
        int nochosei = best(values,weights,i-1,cap);
        int chosei = 0;
        if(cap>=weights[i])
        chosei = values[i]+best(values,weights,i-1,cap-weights[i]);
        int max = Math.max(chosei,nochosei);
        return max;
    }
}

动态规划

动态规划要注意自底向上去写，其实当我们想要求得dp[i][j]的值时，需要知道dp[i-1][j]，这个好说，就是知道上一行的值，那么dp[i-1][j-w(i)]其实也就是需要我们要知道当前列左边的所有值（如果j大于等于w（j）），其实我们在想初始值的时候，可以以这个思路去考虑。
本题初始值就是：

dp[1][w(0)] = v(0),dp[1][w(0)+1]=v(0)...只要容量超过第1个物品，就都取第1个物品。

当我们考虑只可以取一个值的时候，就很简单，如果容量超过他的weight，那么就要他，少于就不要。
代码

 public static int solve01package(int[]values,int[]weights,int C)
    {
        int N = values.length;
        int[][]dp = new int[N+1][C+1];
        //自底向上
        //dp[i][j] = Math.max(dp[i-1][j-w(i)]+v(i),dp[i-1][j])
        //初始值：dp[1][w(0)] = v(0),dp[1][w(0)+1]=v(0)...只要容量超过第1个物品，就都取第1个物品。
        for(int j=0;j<=C;j++)
        {
            if(j>=weight[0])
                dp[1][j] = values[0];
        }
        //从长度为2开始（i=2）
        for(int i=2;i<=N;i++)
        {
            for(int j=1;j<=C;j++)
            {
                int qu = 0;
                //能装下i这个物品
                if(j-weights[i-1]>=0)
                    qu = dp[i-1][j-weights[i-1]]+values[i-1];
                int bq = dp[i-1][j];
                dp[i][j] = Math.max(qu,bq);
            }
        }
        return dp[N][C];
    }

优化空间的动态规划算法

可以通过偶数行和奇数行来简化问题，因为dp[i][j]只和i-1行有关系，因此可以交替赋值，求第2行时，就将第二行的值赋给偶数（第2行），求第三行的时候，就用第2行的值，把第三行的值赋给奇数行（第1行）。这样的空间复杂度为O（2C）。

 public static int solve01package(int[]values,int[]weights,int C)
    {
        int N = values.length;
        int[][]dp = new int[2][C+1];
        //自底向上
        //dp[i][j] = Math.max(dp[i-1][j-w(i)]+v(i),dp[i-1][j])
        //初始值：dp[0][0] = 0,dp[1][w(0)] = v(0),dp[1][w(0)+1]=v(0)...只要容量超过第1个物品，就都取第1个物品。
        for(int j=0;j<=C;j++)
        {
            if(j>=values[0])
                dp[0][j] = values[0];
        }
        //
        //从长度为2开始（i=2）
        for(int i=2;i<=N;i++)
        {
            for(int j=1;j<=C;j++)
            {
                int qu = 0;
                //能装下i这个物品
                if(j-weights[i-1]>=0)
                    qu = dp[i%2][j-weights[i-1]]+values[i-1];
                int bq = dp[i%2][j];
                dp[(i+1)%2][j] = Math.max(qu,bq);
            }
        }
        return dp[(N+1)%2][C];
    }

进一步优化：

尝试只使用一维数组。这里借用一下bobo老师的视频中的图。假如我们当前已经知道了第一行，现在想求第二行的数值，那么我们可以从后往前求（也可以从前往后求，就是要注意从哪一列开始），从后往前求可以确认从哪里停止。
假设我们求解dp[2][5],也就是现在可以存前两个物品，容量为5，我们怎么求最好，要么不要第二个物品（dp[1][5]），要么要这个物品，但背包剩余容量得减去当前数的重量（dp[1][5-w[2]]+v[2]）,比较大小即可。从后往前，直到dp[2][1],容量为1装不下重量为2的这个物品。
这时有人问了，那我容量为1和容量为0怎么办啊，就还和之前一样咯。

代码：

public static int solve01package(int[]values,int[]weights,int C)
    {
        int N = values.length;
        int[]dp = new int[C+1];
        //自底向上
        //dp[i][j] = Math.max(dp[i-1][j-w(i)]+v(i),dp[i-1][j])
        //初始值：dp[0][0] = 0,dp[1][w(0)] = v(0),dp[1][w(0)+1]=v(0)...只要容量超过第1个物品，就都取第1个物品。
        for(int j=0;j<=C;j++)
        {
            if(j>values[0])
                dp[j] = values[0];
        }
        //尝试空间为C
        //从长度为2开始（i=2）
        for(int i=2;i<=N;i++)
        {
            //从后向前
            for(int j=C;j>=weights[i-1];j--)
            {
                int qu = dp[j-weights[i-1]]+values[i-1];
                int bq = dp[j];
                dp[j] = Math.max(qu,bq);
            }
        }
        return dp[C];
    }

完全背包问题：

有N种物品和一个容量为V的背包，每种物品都有无限件可用。第i种物品的费用是c[i]，价值是w[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量，且价值总和最大。

初始思路

他可以取0件，甚至取很多件。

f[i][v]代表前i个值容量为v的最大价值
f[i][v]=max{f[i-1][v-k*c[i]]+k*w[i]|0<=k*c[i]<=v}

我们的第一思路是要把它转换成0-1背包问题，

f(i,v) = max( (f(i-1,v),f(i-1,v-c[i])+w[i],f(i-1,v-2*c[i])+2*w[i]...))
可以看出前面为不取，后面为取1,2,...money/coins[i]个。

拆分成多个0-1背包问题。
伪代码如下：

for i=1:N
	for cap = 1:V
		dp[i][cap]=dp[i-1][cap]
		//取num个i
		for num = 1:cap/c[i-1]
			dp[i][cap] = Math.max(dp[i][cap],dp[i-1][cap-num*c[i-1]]+w[i-1]*num)

很明显算法复杂度为O（V^2N）

O（VN）算法

我们以物品为容量为[1,2,5]为例，考虑dp[i][j]代表前i个值，能组合成j的个数。j我们在考虑设置为5。
会发现dp[2]开头的只与其上一行的一个值，以及上一行左边距离她间隔为2的单元格的值有关。
也就是说以dp[2][5] = (dp[1][5]+dp[1][3]+dp[1][1])红色的值，只与上面粉色的值有关。

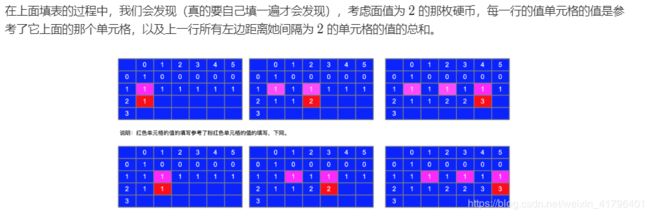
同时，我们在看dp[2][3] = (dp[1][3]+dp[1][1]),这里其实默认dp[2][3]已经考虑了拿一个nums[1]这个数。dp[2][3] = dp[2][1]+dp[1][3],dp[2][1]就代表选取一个nums[1]，剩下的3-2，就使用前面已经分好的答案。
那么可以想到dp[2][5] = dp[2][3]+dp[1][5],这里dp[2][3]代表选取了一个nums【1】，dp[1][5]代表不选nums[1]。

回到完全背包问题

for i = 1：N
	for v = 1..v
		dp[i][v] = dp[i-1][v]
		if(v>coins[i-1])
			dp[i][v] = Math.max(dp[i][v],dp[i][v-c[i-1]]+w[i-1]);

这里其实就是每次都考虑只取一个w[i-1]这个值，但前面的可能取了多个w[i-1]这个值，比如dp[2][3] = Math.max(dp[1][3],dp[2][1]+w[1]),此时dp[2][3]可能就取了后面的值，这样的话，其实已经选取了一个w[i-1]也就是w[1]，dp[2][5] = Math.max(dp[1][5],dp[2][3]+w[1]),此时虽然是取了1个w【1】,但dp[2][3]又取了一个w（1），也就是说此时的dp[2][5]是将不取w[1],和取两个w[2]的情况进行比较。
这也就是为什么要将v从小到大遍历，因为虽然当前这一次只取一个w[i-1],但前面可能取了多次。
最后补充一下背包九讲里说的：

也就是说也可以先循环钱数，在循环每个物品。这里要注意一下，你在做下面的题目会有深刻体会。有的题可以换顺序，有的题目不可以换顺序。

相关题目：

1.分割等和子集背包问题的最好练手题
2.零钱兑换完全背包问题。
3.组合总数IV很好的一道dp题。
4.一和零0-1背包问题多容量条件
5.单词拆分完全背包问题。
6.零钱兑换 II完全背包问题，
7.目标和：0-1背包问题，需要注意容量的范围。
8.抛掷硬币:0-1背包问题。

总结（至关重要）

1.0-1背包问题中，dp数组如果想要约束一维的话，一定要从后往前去走。因为如果从前往后去走会导致，dp[j]已经变成了i+1行的值，而之后在需要dp[j]的时候，代入的值已经是i+1行的了，而不是i行的。

2.要注意题目不会直接是对应的背包问题，所以要根据不同题型来不同对待，简单来说，如果是0-1背包问题就要看看是不是容量变了，或者最终目标变化了。

3.对应完全背包问题，就用下面的公式即可，不用担心取多个背包中物品的情况，因为和0-1背包问题不同的是，我们用的是相同行的元素。

for i = 1：N
	for v = 1..v
		dp[i][v] = dp[i-1][v]
		if(v>coins[i-1])
			dp[i][v] = Math.max(dp[i][v],dp[i][v-c[i-1]]+w[i-1]);

dp[i][v-c[i-1]]考虑的是前i个物品，背包容量为v-c[i-1]，可以取多个物品的情况下所能获得的最大收益。
而dp[i][v-c[i-1]]+w[i-1]代表当前v容量仅考虑再取一件第i个物品，剩下的v-c[i-1]容量的计算之前已经完成了。

//0-1背包问题
dp[i-1][v-c[i-1]]+w[i-1]
//完全背包问题
dp[i][v-c[i-1]]+w[i-1]

也别想着什么颠倒物品和容量的顺序，因为颠倒顺序可能对应不同的题就不一定对了。具体问题一定要具体分析，不要生套公式，如何看两个顺序是否都可以，可以简单看先取1再取2和先取2再取1有没有区别，如果没有的话就是两个顺序都可以，否则就要具体分析。

以零钱兑换的一和二举例：零钱兑换1是要找出组成要求钱数的最少硬币数，因此先取谁后取谁都可以，所以先遍历物品或先遍历钱都可以。

而零钱兑换二要找出可以组成目标钱数的个数，所以先取谁后取谁是相同的，因此要有顺序之分，不能重复计算。

amount = 5, coins = [5，2，1] ，coin=5作为组合的开头只有一种 5=5，之后就不再出现，只能使用面额【2,1】作为硬币组合的开头，硬币按面额5->2->1的顺序使用，但不能回头。在使用面额为coin=2作为硬币组合的开头的时候，可以有2+2+1 ，2+1+1+1的组合，使用完coin=2之后，只剩下了面额【1】，不能再使用面额2，让coin=1作为硬币组合的开头，就只有1+1+1+1+1。 所以应该将物品遍历放在最外层，防止重复。

int[] dp = new int[amount + 1];
    dp[0] = 1;
    for (int coin : coins) {//物品遍历，分别以5,2,1作为硬币组合的开头，以硬币coin=2作为开头时，有2+2+1，2+1+1+1 这两种情况
        for (int i = coin; i <= amount; i++) {//容量扩增
            dp[i] += dp[i - coin];
        }
    }

4.背包问题的核心就是转换为要或者不要，所以无论是0-1背包问题的优化空间，还是完全背包问题的不考虑拿1个拿2个拿3个当前物品。都可以转换为，当前要，或者当前不要，切记都是要1个。

4.LIS问题（最长上升子序列）

相关题目

1.最长上升子序列
2.摆动序列

总结

最长上升子序列的问题，就是考虑以当前i为子序列的尾部（子序列一定要包含i），能组成的最长子序列。其中想满足最长或者摆动就要看题意来写最优子结构，最后要遍历整个dp数组。

5.LOS问题（最长公共子序列）

1.最长公共子序列
2.编辑距离与上一道题不同的就是，上一道题只可以删除，这道题多了其他选择。

总结

最长公共子序列的题目一般是考虑两个字符串，找到他们的满足一些条件的子串。因此一般dp数组需要是二维的，dp[i][j]代表字符串1从【0，i】与字符串2从【0，j】之间满足条件的最长子串。

动态规划总结

1.动态规划的核心点就在于用过去求解好的问题来求解当前的问题，其实不管什么问题都是f(i)与f（i-1）等等之间的关系，所以思路要往这个上面靠。
2.写动态规划题，切忌上来就写代码，先写状态与状态的转移方程，写好之后去写记忆化搜索（递归）的代码。
3.在写递归的代码过程中建议先写常规，后写初始条件，常规就是我们的转移方程，初始条件就是一些可以退出递归的判断条件，一般都是数组或者字符串到了第0个的时候需要给出一个最初始的结果（如下图的if（i==0）），其他的条件就是退出循环的一些越界条件（如下图的if(i<0)）。
一个标准的递归代码如下，我们的主函数（可以这么理解），就直接返回我们写的递归函数的结果就可以，其他什么都不要做。
然后在递归函数中先写常规，在写初始条件。当然这样的递归函数是不可以通过的，我们再在这个基础上补充记忆数组即可。

class Solution {
    public int findTargetSumWays(int[] nums, int S) {
        /* 0-1背包问题，只是这里是取-和取+,f(i,s)代表前i+1能凑成s的个数
        如果当前取-号，那么就是从[0,i-1]去凑S+nums[i],如果取+号，那么就是[0,i-1]去凑S-nums[i]
        f(i,s) = f(i-1,s+nums[i])+f(i-1,s-nums[i])
        */
        return find(nums,nums.length-1,S);
    }
    public int find(int[]nums,int i,int s)
    {
        if(i<0)
            return 0;
        if(i==0){
            //正负都可以
            if(nums[i]==Math.abs(s))
                return 1;
            else 
                return 0;
        }
        //常规
        int result = find(nums,i-1,s+nums[i])+find(nums,i-1,s-nums[i]);
        //System.out.println("result= "+result+","+"i: "+i+",s: "+s);
        return result;
   }
}

4.写完递归与记忆化搜索，我们就大概知道了这个问题的初始条件，就可以用来作为我们dp数组的一些初始赋值。

题解汇总

1.石子游戏

作为一个dp菜鸟，所以把注释写的很详细，大家可以看我的注释，评论区大神们注释写的比较少，希望大家看完我得代码能有所收获。看dp代码最重要的就是要从头到尾推一下dps这个数组的值，你推着推着就明白这个的过程。

class Solution {
    public boolean stoneGame(int[] piles) {
        //dp其实就是存储了递归过程中的数值
        //dps[i][j]代表从i到j所能获得的最大的绝对分数
        //（比如为1就说明亚历克斯从i到j可以赢李1分）
        //如何计算dps[i][j]呢:max(piles[i]-dp[i+1][j],piles[j]-dp[i][j-1]);
        //这里减去dps数组是因为李也要找到最大的
        //最后dps=[5 2 4 1]
        //        [0 3 1 4]
        //        [0 0 4 1]
        //        [0 0 0 5]
        int n=piles.length;
        int [][]dps=new int[n][n];
        //dps[i][i]存储当前i的石子数
        for(int i=0;i<n;i++)
            dps[i][i]=piles[i];
        //d=1,其实代表，先算两个子的时候
        for(int d=1;d<n;d++)
        {
            //有多少组要比较
            for(int j=0;j<n-d;j++)
            {
                //比较j到d+j
                dps[j][d+j]=Math.max(piles[j]-dps[j+1][d+j],piles[d+j]-dps[j][d+j-1]);
            }
        }
        return dps[0][n-1]>0;
    }
}

2.最小路径和

类似于石子游戏

class Solution {

    public int minPathSum(int[][] grid) {
    
        int deepth=grid.length;
        int right=grid[0].length;
         int[][]dps=new int[deepth][right];
        dps[0][0]=grid[0][0];
        //dps[i][j]代表从原点0,0到该点的距离
        for(int i=0;i<deepth;i++)
        {
            for(int j=0;j<right;j++)
            {
                //第一行
                if(i==0&j>0)
                    dps[i][j]=dps[i][j-1]+grid[i][j];
                //第一列
                else if(j==0&&(i>0))
                    dps[i][j]=dps[i-1][j]+grid[i][j];
                else if(i>0&&(j>0))
                    dps[i][j]=Math.min(dps[i-1][j]+grid[i][j],dps[i][j-1]+
                                      grid[i][j]);
            }
         }
        return dps[deepth-1][right-1];
    }
    
}

3.三角形最小路径和

注意从下向上,原地修改triangle。

class Solution {
    public int minimumTotal(List<List<Integer>> triangle) {
        //自底向上，以题中为例。
        //从倒数第二层开始计算
        //6能选择的为4,1，最小的为7，5能选择的为1,8，最小的和为6,7能选择的为8,3，最小路径和为10
        //因此三角形变为
        // 2
        //3  4
      //7  6  10
      //同理继续选择。
      for(int i = triangle.size()-2;i>=0;i--)
      {
          //其实空间应该为常数级别，因为写这两个list只是为了下面写着方便
          List<Integer>now = triangle.get(i);
          List<Integer>down = triangle.get(i+1);
          int size = now.size();
          for(int k=0;k<size;k++)
          {
            //默认应该是当前now的头部，因为每次会删除头部，下一次判断的元素就是now的头部
            int curr = now.get(0);
            int left = down.get(k);
            int right = down.get(k+1); 
            //每次都是删除第一个元素，因为当删除第一个元素之后，下一个要判断的元素就变成当前list的第一个元素了
            now.remove(0);
            int min = Math.min(curr+left,curr+right);
            now.add(min);
            //如果不好理解可以把这个注释打开
            //System.out.println(now);
          }
           
      }
    
      return triangle.get(0).get(0);
    }
}

4.下降路径最小和

加强版的三角形最小路径和，同样用到从下往上找的方法。

class Solution {
    public int minFallingPathSum(int[][] A) {
     //dps[i][j]代表从i这个数到j层的最大值，
        //从下往上找
        //然后判断（dps[0][A[0].length-1]）第一行的每个值到最下面一层中的最小值。
        int [][]dps=new int [A.length][A[0].length];
        for(int j=0;j<A[0].length;j++)
        {
            dps[A.length-1][j]=A[A.length-1][j];
        }
        for(int i=A.length-2;i>=0;i--)
        {
            for(int j=0;j<A[0].length;j++)
            {
             int a1=Integer.MAX_VALUE;
                int a2=Integer.MAX_VALUE;
                int a3=Integer.MAX_VALUE;
                if(j-1>=0)
                    a1=dps[i+1][j-1];
                if(j+1<A[0].length)
                    a2=dps[i+1][j+1];
                a3=dps[i+1][j];
                int a4=Math.min(a2,a3);
                dps[i][j]=Math.min(a1,a4)+A[i][j];
                }
            }
         int min=Integer.MAX_VALUE;
        for(int j=0;j<A[0].length;j++){
            if(dps[0][j]<min)
            {
                min=dps[0][j];
            }
        }
        return min;
        }
       
    }

5.不同路径

1.自顶向下（记忆化搜索）

class Solution {
    int[][]memo;
    public int uniquePaths(int m, int n) {
        //写一下自顶向下的
        //finih(m-1,n-1),只能由左边（m-1,n-2）与上面（m-2,n-1）走到
        //也就是说result(m,n) = result(m,n-1)+result(m-1,n)
        memo = new int[m][n];
        return find(m-1,n-1); 
    }
    public int find(int m,int n)
    {
        if(memo[m][n]!=0)
            return memo[m][n];
        if(m==0||n==0)
        {
            memo[m][n]=1;
            return memo[m][n];
        }
        memo[m][n] = find(m,n-1)+find(m-1,n);
        return memo[m][n];
    }
}

2.自底向上（动态规划）

这个题里由于机器人只能向右走或者向下走，所以我们可以先赋值第一行和第一列为1，然后从dps[1][1]开始赋值，就是该位置的上一个的值+下一个的值，具体看代码。

class Solution {
    public int uniquePaths(int m, int n) {
        //这个题里由于机器人只能向右走或者向下走，所以我们可以先赋值第一行和第一列为1，然后从dps[1][1]开始赋值，就是该位置的上一个的值+下一个的值，具体看代码。
        //m=1,n=1这种情况好迷阿,为啥不是0.
        if(m==1&&n==1)
            return 1;
        int [][]dps=new int[n][m];
        dps[0][0]=0;
        for(int i=1;i<n;i++)
        {
            dps[i][0]=1;
        }
        for(int j=1;j<m;j++)
        {
            dps[0][j]=1;
        }    
        for(int i=1;i<n;i++)
        {
            for(int j=1;j<m;j++)
            {
                dps[i][j]=dps[i-1][j]+dps[i][j-1];
            }
        }
        return dps[n-1][m-1];
    }
}

6.不同路径二

这题主要就是需要注意最开始为1，还有就是第一行和第一列在赋值的时候，如果遇到1，后面的就都不赋值了。

class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
       //这题主要就是需要注意最开始为1，还有就是第一行和第一列在赋值的时候，如果遇到1，后面的就都不赋值了。
        int rows=obstacleGrid.length;
        int columns=obstacleGrid[0].length;
        int [][]dps=new int[rows][columns];
       //最开始就是1([[1,0]])这种情况输出0
        if(obstacleGrid[0][0]==1)
                return 0;
        if(rows==1&&columns==1)
        {
            
    
                return 1;
        }
        for(int i=1;i<rows;i++)
        {
            if(obstacleGrid[i][0]==1)
                break;
            else
                dps[i][0]=1;
        }
        for(int j=1;j<columns;j++)
        {
             if(obstacleGrid[0][j]==1)
                break;
            else
                dps[0][j]=1;
        }
        for(int i=1;i<rows;i++)
        {
            for(int j=1;j<columns;j++)
            {
                if(obstacleGrid[i][j]==1)
                    dps[i][j]=0;
                else
                    dps[i][j]=dps[i-1][j]+dps[i][j-1];
            }
        }
        return dps[rows-1][columns-1];
    }
}

7.整数拆分

这道题也是很经典的理解动态规划的，要注意的写在注释里了。

自顶向下：记忆化搜索。

class Solution {
    int[]memo;
    public int integerBreak(int n) {
        memo = new int[n+1];
        //n可以看成被分为（1，n-1）,(2,n-2),(3,n-3)...（n-1,1）
        //是两部分而非两个数，比如n-1还可以继续分割为（1，n-2）,（2，n-3）...
        return find(n);
    }
    //记忆化搜索
    public int find(int n)
    {
        if(memo[n]>0)
            return memo[n];
        if(n==1)
        {
            memo[1] = 1;
            return 1;
            }
        int max = Integer.MIN_VALUE;
        for(int i=1;i<n;i++)
        {
            //这里一个是拆分的，一个是不拆分的，比如这里只拆分right，不拆分left。
            //不能两个都拆分。
            int left = i;
            //int left = find(i);
            int right = find(n-i);
            //这里注意left，right也可以不拆分,所以要加上这种可能性
            max = Math.max(i*(n-i),Math.max(max,left*right));
        
        }
        memo[n] = max;
        return memo[n];
    }
}

自底向上：动态规划

class Solution {
    public int integerBreak(int n) {
        //使用dp数组来存储n时的乘积最大化
        int []dps=new int[n+1];
        //这几个是没用的，但是为了让大家了解这个。
        //2<=n<=58
        dps[0]=0;
        dps[1]=0;
        //以下才是有用的
        dps[2]=1;
        for(int i=3;i<=n;i++)
        {
            for(int j=2;j<i;j++)
            {
                //我们可能理解比如3拆分为1*dps[2]应该为最大，因为这里dps[2]
                //已经是将2拆分为最大了，但是有可能1*2更大，所以需要比较一下。
                dps[i]=Math.max(dps[i],Math.max(dps[j]*(i-j),j*(i-j)));
            }
        }
        return dps[n];
    }
}

8.最长数对链

这道题主要是可能想不到思路。注释已经写的很清晰，详情看代码。

class Solution {
    public int findLongestChain(int[][] pairs) {
        //首先对数组排序，以pairs[0]的大小从小到大排序。
        //dps[i]代表以pairs[i]为数对链的尾巴的最大数对链长度。
        //假设之前的链尾巴为pairs[i]，
        //核心思想：pairs[j][0]>pairs[i][1],那么就可以把pairs[j]连在pairs[i]的后面。
        int[]dps=new int[pairs.length];
        //最少的数对链是它们自己，所以长度最短都是1。
        Arrays.fill(dps,1);
        //以我用compareTo的理解就是最后的顺序是a[0]-b[0]<0
        //所以是从小到大的排序。
        Arrays.sort(pairs,(a,b)->a[0]-b[0]);
        //从第二个去寻找。
        for(int j=1;j<pairs.length;j++)
        {
            //从第一个去寻找,直到j-1个，因为j+1的第一个数字就比j的第一个数字大，那么
            //j+1的第二个数字肯定就比j的第一个数字大，所以，j不可能是j+1后面的数对。
            for(int i=0;i<j;i++)
            {
                if(pairs[j][0]>pairs[i][1])
                {
                    //去比较每个可能连接pairs[j]的数对，取最大的。
                    dps[j]=Math.max(dps[j],dps[i]+1);
                }
            }
        }
        //判断以每个数对为结尾的数对链中的最大值。
        int max=Integer.MIN_VALUE; 
        for(int i=0;i<dps.length;i++)
        {
            if(dps[i]>max)
                max=dps[i];
        }
        return max;
    }
}

9.买卖股票的最佳时机含手续费

这一道题复杂之处在于可能想不出dp数组的含义。

class Solution {
    public int maxProfit(int[] prices, int fee) {
        //参考评论区
        //dp数组为第i天的最大利润
        //dp思路就是定义两个维度,第一个维度是天数，第二个维度是是否持有,
        //0为不持有，1为持有
        int length=prices.length;
        if(length==0)
            return 0;
        int [][]dp=new int [length][2];
        dp[0][0]=0;
        dp[0][1]=-prices[0];
        for(int i=1;i<length;i++)
        {
            //两种情况i-1天持有，i天卖出
            //i-1天也没有，i天也没有
            dp[i][0]=Math.max(dp[i-1][0],dp[i-1][1]+(prices[i]-fee));
            //两种情况，i-1天持有，i天还持有，
            //i-1天不持有，i天买入
            dp[i][1]=Math.max(dp[i-1][1],dp[i-1][0]-prices[i]);
        }
        //最后一天不持有。
        return dp[length-1][0];
            
    }
}

10.计算各个位数不同的数字个数

首先要注意是各位数字都不同。之后来详解一下dp[i]=dp[i-1]+(dp[i-1]-dp[i-2])*(10-(i-1));

• 加上dp[i-1]没什么可说的，加上之前的数字；dp[i-1]-dp[i-2]的意思是我们之前判断各位不重复的数字我们要在这些数字后面填新的数字。
• 当i=2时，说明之前选取的数字只有1位，那么我们只要与这一位不重复即可，所以其实有9(10-1)种情况（比如1，后面可以跟0,2,3,4,5,6,7,8,9）。
• 当i=3时，说明之前选取的数字有2位，那么我们需要与2位不重复，所以剩余的有8（10-2）种（比如12，后面可以跟0,3,4,5,6,7,8,9）。

class Solution {
    public int countNumbersWithUniqueDigits(int n) {
       
        if(n==0)
            return 1;
        int []dp=new int [n+1];
        dp[0]=1;
         dp[1]=10;
        for(int i=2;i<=n;i++)
        {
            dp[i]=dp[i-1]+(dp[i-1]-dp[i-2])*(10-(i-1));
        }
        return dp[n];
    }
}

11.使用最小花费爬楼梯

经典中的经典，不过这道题要注意不要想多了，我最初的想法是用两个数组去记录从第一层开始的和第二层开始的，其实不需要的。

class Solution {
    public int minCostClimbingStairs(int[] cost) {
        int[]dp=new int[cost.length];
        dp[0]=cost[0];
        dp[1]=cost[1];
        for(int i=2;i<cost.length;i++)
        {
            //一次和两次
            dp[i]=Math.min(dp[i-1]+cost[i],dp[i-2]+cost[i]);
        }
        //可以从倒数第二层直接迈两步
        //也可以从最后一层迈一步
        //return dp[cost.length-1]; 
        return Math.min(dp[cost.length-1],dp[cost.length-2]);
    }
}

12.只有两个键的键盘

初始的方法，我们去寻找因子来找到更快的方式。

class Solution {
    public int minSteps(int n) {
        int []dps=new int[n+1];
        dps[1]=0;
        //使用n的因子来处理
        for(int i=2;i<=n;i++)
        {
            dps[i]=i;
            for(int j=2;j<i;j++)
            {
               if(i%j==0)
               {
                   //i-j的意思是现在已经有j了，所以要减去，需要再粘贴（i-j）/j
                   //个j，然后+1是加上copyAll的这一次
                   dps[i]=Math.min(dps[i],dps[j]+(i-j)/j+1);
               }
            }
        }
        return dps[n];
    }
}

改进版，直接去找最大的因子即可

class Solution {
    public int minSteps(int n) {
        int []dps=new int[n+1];
        dps[1]=0;
        //使用n的因子来处理
        for(int i=2;i<=n;i++)
        {
            dps[i]=i;
            for(int j=i-1;j>0;j--)
            {
               if(i%j==0)
               {
                   //i-j的意思是现在已经有j了，所以要减去，需要再粘贴（i-j）/j
                   //个j，然后+1是加上copyAll的这一次
                   dps[i]=Math.min(dps[i],dps[j]+(i-j)/j+1);
                   break;
               }
            }
        }
        return dps[n];
    }
}

13.预测赢家

这里主要需要注意的有两点：

1. 两个玩家相等，玩家一仍然胜利。
2. 对于dp二维数组首先赋值一个数，之后去计算的是之间相差两个数，之后计算中间相差三个数，以此类推。

比如 nums=【1,2,3,4】，意思就是说先去计算（12,23，34），之后去计算（13，24）

class Solution {
    public boolean PredictTheWinner(int[] nums) {
         int n=nums.length;
        int [][]dps=new int[n][n];
        //dps[i][i]为玩家一从i到i赢得，肯定只能是nums【i】
        for(int i=0;i<n;i++)
            dps[i][i]=nums[i];
        //d=1,其实代表，先算两个数的时候
        for(int d=1;d<n;d++)
        {
            //有多少组要比较
            for(int j=0;j<n-d;j++)
            {
                //比较j到d+j
                //其实意思就是比较j到d+j时，玩家1，只能选择两端的，
                //玩家一选择了j时，那么玩家二就从j+1到d+j中选最大的。
                //玩家一选了d+j时，那么玩家二就从j到d+j-1中选最大的
                dps[j][d+j]=Math.max(nums[j]-dps[j+1][d+j],nums[d+j]-dps[j][d+j-1]);
            }
        }
        //两个玩家相等，玩家一仍然胜利。
        return dps[0][n-1]>=0;
    }
}

14.最长回文子序列

这里是你没体验过的超全超详细讲解。 dp[i][j]代表从i到j的最长的回文子串，更改dp二维矩阵的上三角，我们是斜着去更改数值的，不是一行一列那样去更改的。

class Solution {
    public int longestPalindromeSubseq(String s) {
        //dp[i][j]代表从i到j的最长的回文子串
        //更改dp二维矩阵的上三角，
        //我们是斜着去更改数值的，不是一行一列那样去更改的。
        int length=s.length();
        if(length==0)
            return 0;
        int[][]dp=new int[length][length];
        //长度此时为1，赋值都是1。
        for(int i=0;i<length;i++)
        {
            dp[i][i]=1;
        }
        //从n+1（2）长度开始
        for(int n=1;n<length;n++)
        {
            //从第一行(i=0)开始，有几（lenth-n）组(长度为n+1)的就循环几次
            for(int i=0;i<length-n;i++){
                //首先要注意，不是判断i+n和i+n-1,这个题不需要连续。
                if(s.charAt(i)==s.charAt(i+n))
                {
                    //这里＋2的意思就是说，我的首和尾相等了，那长度肯定可以加上这两个
                    //再加上从i+1到n+i-1这段的最长回文子序列数量。
                    dp[i][n+i]=dp[i+1][n+i-1]+2;
                }
                else
                {
                //判断dp[首+1，尾]，和dp[首，尾-1]。取其最大值。
                    dp[i][n+i]=Math.max(dp[i+1][n+i],dp[i][n+i-1]);
                }
            }
        }
        return dp[0][length-1];
    }
}

15.最长回文子串

class Solution {
    public String longestPalindrome(String s) {
        //与最长回文子序列相似，不过要加上一个数组用于判断是否为回文子串
        int length=s.length();
        if(length==0||length==1)
            return s;
        int start=0;
        int maxlength=1;
        boolean [][]dp=new boolean[length][length];
        //还是从1的长度开始一直到length-1。
        for(int i=0;i<length;i++)
        {
            dp[i][i]=true;
        }
        //2的长度
        for(int i=0;i<length-1;i++)
        {
            if(s.charAt(i)==s.charAt(i+1))
            {
                dp[i][i+1]=true;
                start=i;
                maxlength=2;
            }
        }
        //3的长度和更多长度
        for(int i=2;i<length;i++)
        {
            for(int j=0;j<length-i;j++)
            {
                
                if(s.charAt(j)==s.charAt(i+j)&&dp[j+1][i+j-1]==true)
                {   
                    //如果比最大值大再更改起始位置和最大长度
                    if(i>maxlength-1)
                {start=j;
                    maxlength=i+1;
                }
                    //不管大不大我们都要去更改dp数组，好告诉这一段是回文的
                    dp[j][i+j]=true;
                }
            }
        }
        return s.substring(start,start+maxlength);
    }
}

16.组合总数IV

class Solution {
    public int combinationSum4(int[] nums, int target) {
        //dfs会超时
        //使用dp数组，dp[i]代表组合数为i时使用nums中的数能组成的组合数的个数
        //别怪我写的这么完整
        //dp[i]=dp[i-nums[0]]+dp[i-nums[1]]+dp[i=nums[2]]+...
        //举个例子比如nums=[1,3,4],target=7;
        //dp[7]=dp[6]+dp[4]+dp[3]
        //其实就是说7的组合数可以由三部分组成，1和dp[6]，3和dp[4],4和dp[3];
        int[]dp=new int[target+1];
        //是为了算上自己的情况，比如dp[1]可以有dp【0】+1的情况。
        dp[0]=1;
        for(int i=1;i<=target;i++)
        {
            for(int num:nums)
            {
                if(i>=num)
                {
                    dp[i]+=dp[i-num];
                }
            }
        }
        return dp[target];
    }
}

17.最长重复子数组

class Solution {
    public int findLength(int[] A, int[] B) {
        //注意，不是以A的前i个元素和B的前j个元素的公共子数组的最大长度
        //dp[i][j]为A以A[i-1]这个元素为结尾,B以B[j-1]这个元素为结尾的子数组的长度。
        //那么A[i-1]!=B[j-1]，dp[i][j]=0;
        //A[i-1]==B[j-1],dp[i][j]=dp[i-1][j-1]+1;
        int[][] dp=new int[A.length+1][B.length+1];
        dp[0][0]=0;
        int max=0;
        for(int i=1;i<=A.length;i++)
        {
            for(int j=1;j<=A.length;j++)
            {
                if(A[i-1]==B[j-1])
                {
                    dp[i][j]=dp[i-1][j-1]+1;
                    max=Math.max(max,dp[i][j]);
                }
            }
        }
        return max;
    }
}

18.完全平方数

记忆化搜索

这里注意的是在分的时候直接要分成两部分，一个为平方数，另一个为可以拆或直接就是平方数的数。以12举例，只有（1,11），（4,8），（9,3）。但我们在寻找这个平方数的时候不要从1到12的去寻找然后判断每个数是否为平方数，这样循环的次数太多了，以12为例，可以选择的平方数的因子i只有（1,2,3）,那么对于n来说i就是（1,2，3，根号n），对应的数就是i*i。

class Solution {
    int[]memo;
    public int numSquares(int n) {
        memo = new int[n+1];
        //使用自顶向下的方式
        //12可以分成
     //(1,11),(4,8),(9,3)
     //前面的数必须为完全平方数，后面的数可以拆开
        return find(n);
    }
    public int find(int n){
        int genhao = (int)Math.sqrt(n);
        if(memo[n]!=0)
            return memo[n];
        //n本身就是完全平方数
        if(genhao*genhao==n)
        {
            memo[n] = 1;
            return 1;
        }
        //这里最多应该是n（也就是n个1）
        int now = n;
        //我们更换一下循环的
        // for(int i=1;i
        //这种循环太费时间，可以只判断从1到n之间所有的完全平方数(i为完全平方数的根号)
        //从1到n之间可以满足的完全平方数的数为（1,2,3,4,...根号n）对应的为（1,4,9,16）
        for(int i=1;i*i<n;i++)
        {
         now = Math.min(now,1+find(n-i*i));
        }
        memo[n] = now;
        return memo[n];
    }
}

dp算法

实例的解释

dp[0] = 0 
dp[1] = dp[0]+1 = 1
dp[2] = dp[1]+1 = 2
dp[3] = dp[2]+1 = 3
dp[4] = Min{ dp[4-1*1]+1, dp[4-2*2]+1 } 
      = Min{ dp[3]+1, dp[0]+1 } 
      = 1				
dp[5] = Min{ dp[5-1*1]+1, dp[5-2*2]+1 } 
      = Min{ dp[4]+1, dp[1]+1 } 
      = 2
						.
						.
						.
dp[13] = Min{ dp[13-1*1]+1, dp[13-2*2]+1, dp[13-3*3]+1 } 
       = Min{ dp[12]+1, dp[9]+1, dp[4]+1 } 
       = 2
						.
						.
						.
dp[n] = Min{ dp[n - i*i] + 1 },  n - i*i >=0 && i >= 1

代码

class Solution {
    public int numSquares(int n) {
      //dp[n]代表和等于n时，所需要最少的完全平方数。
    //dp[n]=min(dp[n-i*i]+1),n-i*i>=0&&i>=1
    //这里的+1就是加上这个i*i平方数。n-i*i=0就是这个数就是个完全平方数（4）。
        int yinzi = (int)Math.sqrt(n);
        if(yinzi*yinzi==n)
            return 1;
       //尝试自底向上
       int[]dp = new int[n+1];
        dp[1] = 1;
       for(int i=2;i<=n;i++)
       {
           //直接就是完全平方数
           int zi  = (int)Math.sqrt(i);
           if(zi*zi==i)
           {
               dp[i] =1;
               continue;
           }
           int min = i;
           //可以选择的因子
           for(int row = 1;row*row<i;row++)
           {
            min  = Math.min(min,1+dp[i-row*row]);
           }
           dp[i] = min;
       }
       for(int d:dp)
        System.out.println(d);
       return dp[n]; 
    }
}

19.最低票价注意的就是周票有比天票便宜的情况。

class Solution {
    public int mincostTickets(int[] days, int[] costs) {
        //dp【i】代表以days[i]结束所花下的最少花费。
        //先来一个365天的吧
        int[]dp=new int [366];
        int cost1=costs[0];
        int cost7=costs[1];
        int cost30=costs[2];
        dp[0]=0;
        Set<Integer> dayset=new HashSet<>();
        for (int d: days) dayset.add(d);
        for(int i=1;i<366;i++)
        {
          if(!dayset.contains(i))
            dp[i]=dp[i-1];
            else
            {
                int cost=0;
                //存在天票比周票贵的情况
               int number7=Integer.MAX_VALUE;
                int number30=Integer.MAX_VALUE;
                if(i>7)
                {
                    number7=dp[i-7]+cost7;
                }
                else
                    number7=dp[0]+cost7;
                if(i>30)
                {
                    number30=dp[i-30]+cost30;
                }
                else
                    number30=dp[0]+cost30;
                cost=Math.min(Math.min(number7,number30),cost1+dp[i-1]);
                dp[i]=cost;
            }
        }
        return dp[365];
    }
}

20.零钱兑换

思路

很明显，这是一道完全背包问题，和分割等和子集类似，区别就是我可以取多个相同的硬币尝试组合成金额，同时我们不光要判断是否能组合成，还要找到能组合成且所需硬币最少的个数。很明显，我们的状态方程应该如下定义。

		完全背包问题
        f(i,money)为考虑从前i个中选取零钱，能组成amount的最小个数。
        f(i,money) = Math.min(f(i-1,money),f(i-1,money-coins[i])+1,f(i-1,money-2*coins[i])+2...)
        可以看出前面为不取，后面为取1,2,...money/coins[i]个。
        值得注意的就是我们要判断f(i-1,money-coins[i])不为-1，才可以加进来比较。

不过我相信肯定有很多人不会直接思考到这个，我将一步一步带大家从初始的思维向动态规划思维转换。

代码

1.错误思路

我想一定有人用这个思路去做，我做个dfs函数，传入coins数组，传入length（从【0，length】寻找，当前考虑coins【length】拿不拿），money，times（当前拿零钱的个数）
每次找到组合肯定会让当前money为0，那我再设置一个变量min，每次进入money为0的判断，我就与min比较一下取最小值咯。
代码如下：

class Solution {
    int min = -1;
    public int coinChange(int[] coins, int amount) {
        /*完全背包问题
        f(i,money)为考虑拿前i个数是否能补充满money，不过可以拿多个i
        f(i,money) = f(i-1,money)||f(i-1,money-coins[i])||f(i-1,money-2*coins[i])...
        可以看出前面为不取，后面为取1,2,...money/coins[i]
        */
        fullpackage(coins,coins.length-1,amount,0);
        return min;
    }
    public void fullpackage(int[]coins,int length,int money,int times)
    {
        if(money==0){
            //System.out.println(times);
            if(min==-1)
                min = times;
            else{
                min = Math.min(min,times);
            }
            return ;
        }
        if(length<0||money<0)
            return ;
        //只有一个了，一个能不能填满money，就看money能不能整除这一个硬币的金额了。
        if(length==0){
            if(money%coins[0]==0){
                fullpackage(coins,0,0,times+money/coins[0]);
            }
            else
                return ;
        }
        //正常操作
        fullpackage(coins,length-1,money,times);
        for(int i=1;i<=money/coins[length];i++)
        {
            fullpackage(coins,length-1,money-i*coins[length],times+i);
            //System.out.println(i*coins[length]+" "+money);
        }
        return ;
    }
}

结果是什么样我相信大家心里早已有了答案。同时注意一点，代码一定要把你想输出调试的语句注释掉，会影响时间的。

这种思路是传统的DFS思路，思路是完全可行的，但是会超时，大家看到问题所在了么，不管什么样的动态规划问题，第一步一定要考虑他状态方程，与方程的含义，之后才可以写代码。

2.记忆化搜索

整体不难，就是要注意初始条件的判断，dfs中结束递归的条件包括：
1.money为0，说明不需要零钱了，因此返回0,
2.length<0||money<0，肯定要返回-1，因为length<0是没有零钱了，而money<0说明之前选取的不对
3.记忆化数组不为0，直接返回记忆化数组，这个记忆化数组可以为-1，也可以为其他值，就是不可能赋值之后还为0。

class Solution {
    int[][]memo;
    public int coinChange(int[] coins, int amount) {
        /*完全背包问题
        f(i,money)为考虑从前i个中选取零钱，能组成amount的最小个数。
        f(i,money) = Math.min(f(i-1,money),f(i-1,money-coins[i])+1,f(i-1,money-2*coins[i])+2...)
        可以看出前面为不取，后面为取1,2,...money/coins[i]个。
        值得注意的就是我们要判断f(i-1,money-coins[i])不为-1，才可以加进来比较。
        */
        memo = new int[coins.length][amount+1];
        fullpackage(coins,coins.length-1,amount);
        return memo[coins.length-1][amount];
    }
    public int fullpackage(int[]coins,int length,int money)
    {
        //money为0说明不需要再去取零钱就可以满足因此返回0.
        if(money==0){
            return 0;
        }
        if(length<0||money<0)
            return -1;
        if(memo[length][money]!=0)
            return memo[length][money];
        //只有一个了，一个能不能填满money，就看money能不能整除这一个硬币的金额了。
        if(length==0){
            int min = -1;
            if(money%coins[0]==0){
               min =  money/coins[0];
            }
            memo[length][money] = min;
            return memo[length][money];
        }
        //正常操作
        int min = fullpackage(coins,length-1,money);
        for(int i=1;i<=money/coins[length];i++)
        {
            int nowmin = fullpackage(coins,length-1,money-i*coins[length]);
            //这里要注意只有返回值不为-1，才可以加进去比较哦
            if(nowmin!=-1)
            {
                //防止min为-1，为-1就直接把min赋值。
                if(min==-1)
                    min = nowmin+i;
                else
                    min = Math.min(min,nowmin+i);
                }
        }
        memo[length][money] = min;
        return memo[length][money];
    }
}

3.动态规划

二维数组

class Solution {
    public int coinChange(int[] coins, int amount) {
         /*完全背包问题
        f(i,money)为考虑从前i个中选取零钱，能组成amount的最小个数。
        f(i,money) = Math.min(f(i-1,money),f(i-1,money-coins[i])+1,f(i-1,money-2*coins[i])+2...)
        可以看出前面为不取，后面为取1,2,...money/coins[i]个。
        值得注意的就是我们要判断f(i-1,money-coins[i])不为-1，才可以加进来比较。
        */
        int N = coins.length;
        int[][]dp = new int[N][amount+1];
        //初始值dp[i][0]=0(amount=0,肯定需要组成的零钱数为0)
        //初始值dp[0][money]要算一下
        for(int money=0;money<=amount;money++)
        {
            if(money%coins[0]==0)
                dp[0][money] = money/coins[0];
            else 
                dp[0][money] = -1;
        }
        //从coins[i]开始(从长度为2开始)
        for(int i=1;i<N;i++)
        {
            for(int money = 1;money<=amount;money++)
            {
                //不取coins[i]
                dp[i][money] = dp[i-1][money];
                for(int num = 1;num<=money/coins[i];num++)
                {
                    //可以由[0,i-1]组成money-num*coins[i]这个数字
                    if(dp[i-1][money-num*coins[i]]!=-1){
                        //可能之前dp[i-1][money]为-1，所以要区分一下
                        if(dp[i][money]!=-1)
                            dp[i][money] = Math.min(dp[i-1][money-num*coins[i]]+num,dp[i][money]);
                        else
                            dp[i][money] = dp[i-1][money-num*coins[i]]+num;
                    }
                }
            }
        }
        return dp[N-1][amount];
    }
}

一维数组

class Solution {
    public int coinChange(int[] coins, int amount) {
         /*完全背包问题
        f(i,money)为考虑从前i个中选取零钱，能组成amount的最小个数。
        f(i,money) = Math.min(f(i-1,money),f(i-1,money-coins[i])+1,f(i-1,money-2*coins[i])+2...)
        可以看出前面为不取，后面为取1,2,...money/coins[i]个。
        值得注意的就是我们要判断f(i-1,money-coins[i])不为-1，才可以加进来比较。
        */
        int N = coins.length;
        int[]dp = new int[amount+1];
        //使用一维数组
        for(int money=0;money<=amount;money++)
        {
            if(money%coins[0]==0)
                dp[money] = money/coins[0];
            else 
                dp[money] = -1;
        }
        //从coins[i]开始(从长度为2开始)
        for(int i=1;i<N;i++)
        {
            //从后往前走
            for(int money = amount;money>=coins[i];money--){
                for(int num = 1;num<=money/coins[i];num++)
                    {
                        int now = dp[money-num*coins[i]];
                        if(now!=-1){
                            if(dp[money]==-1)
                                dp[money] = now+num;
                            else
                                dp[money] = Math.min(dp[money],now+num);
                        }
                    }       
            }
        }
        return dp[amount];
    }
}

时间竟然比记忆化搜索还大，哭辽。

4.更节省时间的动态规划

这个算法非常聪明，省去了一层循环，直接把时间复杂度降下去很多，他是直接让钱数从1到amount去循环，这个就不考虑当前的包裹到底拿不拿，他考虑的是我当前的钱数只能由coins中的数组成，举例说明：比如amount为11，coins为【1,2,5】，当前钱数为11时，只能由1+10,2+9,5+6组成，而dp【10】，dp【9】，dp【6】我们之前已经算过了，zh

class Solution {
    public int coinChange(int[] coins, int amount) {
        //不能用贪心算法
        //dp[i]代表凑成i的最少硬币数量
        //for coin:coins（每一个coin是一种组成方式）,+1（+1是代表1个硬币）就是加上这个i这个数
        // //dp[i]=Math.min(dp[i],dp[i-coin]+1)
        //实例：
        //比如amount=11时。当coin为1时可以由1和dp【10】，coin为2时，则可以由，2和dp[9]
        //coin为5时，可以由5和dp[6]，比较这三个值谁大，最后会获得dp[11]。如果都不可以组成的话，
        //dp【11】就为-1。
       
        int []dp=new int [amount+1];
        dp[0]=0;
        for(int i=1;i<=amount;i++)
        {
            dp[i]=Integer.MAX_VALUE;
            //判断是否能由零钱构成
            boolean flag=false;
            for(int coin:coins)
            {
                //i要比这个coin值大，且可以组成
                if(i-coin>=0&&dp[i-coin]!=-1)
                {
                    flag=true;
                    dp[i]=Math.min(dp[i],dp[i-coin]+1);
                }
            }
            //不可以由coins数组中的数来组成当前的i。
            if(flag==false)
                dp[i]=-1;
        }
        return dp[amount];
    }
}

5.能看出是完全背包解法的解法

不把物品放外层循环，我都看不出来是完全背包问题，外层j循环的意思就是dp[j][money]，取前j+1个数，组成money的最小个数。

dp[j][money] = Math.min(dp[j-1][money](不取),dp[j][money-coins[j]](取一个))

每次默认取一个，不用担心这不是dp[j][money]的最优值，因为其实dp[j][money-coins[j]]中还会取多个coins[j]，而且dp[j][money-coins[j]]已经是最优解了。

一定要特别注意，如果dp[i-coin]为-1，则说明前j+1个元素无法组成i-coin，那么即使当前的i（money）比coin大也不可取。

if(i-coin>=0&&dp[i-coin]!=-1)

完整代码

class Solution {
    public int coinChange(int[] coins, int amount) {
        int []dp=new int [amount+1];

        for(int i=1;i<=amount;i++){
            if(i%coins[0]==0)
                dp[i] = i/coins[0];
            else
                dp[i] = -1;
        } 
        for(int j=1;j<coins.length;j++){
            for(int i=1;i<=amount;i++)
            {
            //i要比这个coin值大，且可以组成
            int coin = coins[j];
            if(i-coin>=0&&dp[i-coin]!=-1)
            {
                if(dp[i]!=-1)
                    dp[i]=Math.min(dp[i],dp[i-coin]+1);
                else
                    dp[i] = dp[i-coin]+1;
                }
            }
        }
        return dp[amount];
    
}
}

21.乘积最大子序列

注意这里不是这样：设置一个数组dp，dp[i]表示以nums[i]结尾的子序列的最大积，初始状态：
dp[0] = nums[0];
状态转移方程就是： dp[i] = max(dp[i - 1] * nums[i], nums[i])
这样就OK啦！
正确的解法：应该是同时记录最大积和最小积，dp[i][0]表示以nums[i]结尾的子序列的最小积，dp[i][1]表示以nums[i]结尾的子序列的最大积。
初始状态：
dp[0][0] = nums[0];
dp[0][1] = nums[0];
由于可能存在负数，所以有三个数参与判断，状态转移方程：
dp[i][0] = min( min(dp[i - 1][0] * nums[i], dp[i - 1][1] * nums[i]), nums[i])
dp[i][1] = max( max(dp[i - 1][0] * nums[i], dp[i - 1][1] * nums[i]), nums[i])
具体详见代码。

class Solution {
    public int maxProduct(int[] nums) {
        //dp数组代表以i为结尾的最大乘积。
        //因为有负负得正
        //所以要加上最小和最大，就需要二维数组
        //dp[i][0]最小积
        //dp[i][1]最大积
    
        if(nums.length==1)
            return nums[0];
        int [][]dp=new int [nums.length][2];
        int max=nums[0];
        //防止第一个最大
       // int max=Integer.MIN_VALUE;
        dp[0][0]=nums[0];
        dp[0][1]=nums[0];
        for(int i=1;i<nums.length;i++)
        {
            dp[i][0]=Math.min(Math.min(dp[i-1][0]*nums[i],dp[i-1][1]*nums[i]),nums[i]);
            dp[i][1]=Math.max(Math.max(dp[i-1][0]*nums[i],dp[i-1][1]*nums[i]),nums[i]);
            if(dp[i][1]>max)
                max=dp[i][1];
        }
        return max;
    }
}

22.最小路径和

本题相对来说比较简单，可以直接写出自底向上的动态规划解法。

class Solution {
    public int minPathSum(int[][] grid) {
        //dp[i][j]代表从0,0到i,j的最短路(（i，j）只能从其上面（i-1,j）或左面(i,j-1)走到)
        //dp[i][j] = Math.min(grid[i][j]+dp[i-1][j],grid[i][j]+dp[i][j-1])
        if(grid==null||grid.length==0)
            return 0;
        int[][]dp = new int[grid.length][grid[0].length];
        dp[0][0] = grid[0][0];
        //第一行只能从左到右走
        for(int j=1;j<grid[0].length;j++)
        {
            dp[0][j]+=dp[0][j-1]+grid[0][j];
        }
        //第一列只能从上往下走
        for(int i=1;i<grid.length;i++)
        {
            dp[i][0]+=dp[i-1][0]+grid[i][0];
        }
        //
        for(int i=1;i<grid.length;i++)
        {
            for(int j=1;j<grid[0].length;j++)
            {
                dp[i][j] = Math.min(dp[i-1][j]+grid[i][j],dp[i][j-1]+grid[i][j]);
            }
        }
        return dp[grid.length-1][grid[0].length-1];
    }
}

23.打家劫舍

第一种状态：f(x)定义为考虑偷取[x…n)所能获取的最大利益

自顶向下：记忆化搜索

首先可以画出一个图。当考虑偷取【0,…,n-1】范围的所有房子，可以穷举所有方式：
（1）偷取0，之后从【2…n-1】去偷取，（2）偷取1，之后去【3…n-1】…（n）偷取n-1。
注意：偷取【2…n-1】范围的所有房子还可以继续分成多种情况，依次类推。
因此：状态的定义:考虑偷取【x,…n-1】范围里的房子。
转移方程：以x=0为例
f(0) = max{
v(0)+f(2),v(1)+f(3),v(2)+f(4),…v(n-3)+f(n-1),v(n-2),v(n-1)
}
注意这里涉及一个点：【3,1，2,4】，偷取0号房子和3号房子是最优解，而思维误区可能是我偷取完0号房子不能偷相邻的就去偷2号房子吧，其实不一定。

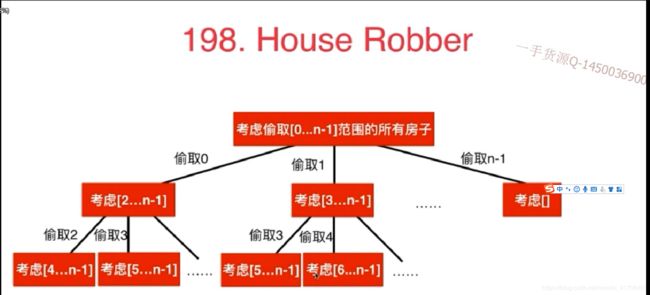
注意这个代码是不可以通过的，但思路是对的。

class Solution {
    int[]memo;
    public int rob(int[] nums) {
        /*
        自顶向下：记忆化搜索
        状态的定义:考虑偷取【x,...n-1】范围里的房子，注意这里不一定要偷取x，也可能偷取x之后的
        转移方程：以x=0为例
        f(0) = max{
            v（0）+f(2)//不能选取相邻的所以选取偷0之后只能从2，n-1去挑选
            v(0)+f(2),v(1)+f(3),v(2)+f(4),...v(n-3)+f(n-1),v(n-2),v(n-1)
            最后两个其实为v(n-2)+f(n),v(n-1)+f(n+1),不过f（n）与f（n-1）没有可以选择的房子了。
        }
        */
        memo = new int[nums.length];
        //注意nums中的数为非负整数，同时存在一个用例全部都是0。
        Arrays.fill(memo,-1);
        return findrob(nums,0);
    }
    //考虑偷取【index,...n-1】范围里的房子
    public int findrob(int[]nums,int index)
    {
        //index,...n-1这个区间已经没有房子可以偷
        if(index>=nums.length)
            return 0;
        if(memo[index]!=-1)
            return memo[index];
        int max = -1;
        /*
        i取值[index-nums.length-1]
        f(index) = max{v(i)+f(i+2)}
        */
        for(int i = index;i<nums.length;i++)
        {
            max = Math.max(max,nums[i]+findrob(nums,i+2));
        }
        memo[index] = max;
        return max;
    }
}

自底向上：动态规划

具体看注释

  //动态规划做法：自底向上
        /*
         f(0) = max{
            v（0）+f(2)//不能选取相邻的所以选取偷0之后只能从2，n-1去挑选
            v(0)+f(2),v(1)+f(3),v(2)+f(4),...v(n-3)+f(n-1),v(n-2),v(n-1)
            最后两个其实为v(n-2)+f(n),v(n-1)+f(n+1),不过f（n）与f（n-1）没有可以选择的房子了。
        }
        子问题其实是f(n-1)，此时只能选取偷n-1,f(n-1) = v(n-1)
        f(n-2) = max{v(n-2)+f(n),v(n-1)+f(n+1)},其实是max（v（n-2）,v(n-1)）
        f(n-3) = max{v(n-3)+f(n-1),v(n-2)+f(n),v(n-1)+f(n+1)}
        */

详细代码：

class Solution {
    public int rob(int[] nums) {
      
        if(nums.length==0||nums==null)
            return 0 ;
        int n = nums.length;
        int[]memo = new int[n];
        memo[n-1] = nums[n-1];
        for(int i=n-2;i>=0;i--)
        {
            int max = -1;
            //偷取v(j)+考虑偷取f(j+2)
            //j的范围为i到n-1
            for(int j=i;j<=n-1;j++)
            {
                int now = nums[j];
                //可能涉及情况为 max{v(n-2)+f(n),v(n-1)+f(n+1)},而f（n）和f（n+1）都为空
                if(j+2<=n-1)
                    now+=memo[j+2];
                max = Math.max(now,max);
            }
            memo[i] = max;
        }
        return memo[0];
    }
}

O（n）时间复杂度

继续更改f(x)定义,f(x)定义为考虑偷取[x…n)所能获取的最大利益。
偷当前的再去偷就要从x+2的房子考虑了，而不偷当前的就从x+1的房子考虑
f(x) = max(nums[x]+f(x+2),f(x+1))

class Solution {
    int[]memo;
    public int rob(int[] nums) {
        //继续更改f(x)定义,f(x)定义为考虑偷取[x...n)所能获取的最大利益。
        //偷当前的再去偷就要从x+2的房子考虑了，而不偷当前的就从x+1的房子考虑
        //f(x) = max(nums[x]+f(x+2),f(x+1))
        memo = new int[nums.length];
        Arrays.fill(memo,-1);
        return find(nums,0);
    }
    /*
        代表考虑偷取[index,n)
        这里不需要赋值，因为最先会进入find(nums,n-1),
        find(nums,n-1) = max(nums[n-1]+find(n+1),find(n))=max(nums[n-1])=nums[n-1],就返回了。
        find(nums,n-2)同理 = max(num[n-2]+find(n),find(n-1)) = max(nums[n-2],nums[n-1])
    */
    public int find(int[]nums,int index)
    {
        
        //当index=n-1或n-2时
        if(index>=nums.length)
            return 0;
        if(memo[index]!=-1)
            return memo[index];
        memo[index] = Math.max(find(nums,index+2)+nums[index],find(nums,index+1));
        return memo[index];
    }
}

第二种状态：f(x)定义为考虑偷取（1，x）之间的屋子所能获得的最大利益

自底向上：动态规划

更改状态定义：f(x)定义为考虑偷取（1，x）之间的屋子所能获得的最大利益
f(n) = max{v(n-1)+f(n-3),v(n-2)+f(n-4),…v(3)+f(1),v(2),v(1)}
这回初始值是memo[1]了，memo[1]=nums[1]，因为（1,1）只能去偷1这间房子。
代码如下：

class Solution {
    public int rob(int[] nums) {
         /*考虑更改状态定义：f(x)定义为考虑偷取（1，x）之间的屋子
        f(n) = max{v(n-1)+f(n-3),v(n-2)+f(n-4),...v(3)+f(1),v(2),v(1)}
        列f（n）的式子是从偷第n-1个屋子开始往后写的，这样便于理解。
        */
        if(nums==null||nums.length==0)
            return 0;
        int n = nums.length;
        int[]memo = new int[n+1];
        memo[1] = nums[0];
        for(int i=2;i<=n;i++)
        {
            //v（j）
            for(int j=i;j>=1;j--)
            {
                int num = nums[j-1];
                if(j-2>=1)
                    num+=memo[j-2];
                memo[i] = Math.max(memo[i],num);
            }
        }
        return memo[n];
    }
}

24.打家劫舍 II

状态定义为f(x)定义为考虑偷取[x…n)所能获取的最大利益

其实区别在于如果偷取第一个房间就不能偷取最后一个房间，那么我们仍然用之前的定义，只不过需要比较从【0…n-2】与【1…n-1】两个范围的最大利益谁比较大。返回较大值。如打家劫舍，我们设置两个memo数组分别用于记忆[0…n-2]与[1…n-1]

class Solution {
    public int rob(int[] nums) {
        /*
        仍然对状态定义为:考虑偷取[x...n-1]范围里的房子，尝试自底向上
        f(0) = max{v(0)+f(2),v(1)+f(3),v(2)+f(4)...v(n-3)+f(n-1),v(n-2),v(n-1)} 
        然而对于偷取了0就不能偷取n-1因此可以设立两个范围，
        max = max{[0...n-2],[1...n-1]}   
        */
        int n = nums.length;
        if(nums==null||nums.length==0)
            return 0;
        if(nums.length==1)
            return nums[0];
        int[]memo1 = new int[nums.length];
        int[]memo2 = new int[nums.length];
        //1...n-1
        memo1[n-1] = nums[n-1];
        //0..n-2
        memo2[n-2] = nums[n-2];
        //0..n-2
        for(int i=n-3;i>=0;i--)
        {
            //偷取j与考虑偷取f(j+2)
            for(int j=i;j<=n-2;j++)
            {
                int now = nums[j];
                if(j+2<=n-2)
                    now+=memo2[j+2];
                memo2[i] = Math.max(memo2[i],now);
            }
        }
        //1...n-1
        for(int i=n-2;i>=1;i--)
        {
            //偷取j与考虑偷取f(j+2)
            for(int j=i;j<=n-1;j++)
            {
                int now = nums[j];
                if(j+2<=n-1)
                    now+=memo1[j+2];
                memo1[i] = Math.max(memo1[i],now);
            }
        }
        return Math.max(memo1[1],memo2[0]); 
    }
}

25.买卖股票的最佳时机

dp算法：自底向上

class Solution {
    public int maxProfit(int[] prices) {
        //考虑[7,1,5,3,6,4]
        //f(x)定义为选择x日买股票,在(x，n)区间卖出可以获得的最大价格。
        //f(0) = max{prices[1]-prices[0],prices[2]-prices[0],...prices[n-1]-prices[0]}
        //max=max{f(0),f(1),f(2),f(3)...f(n-2)}
        //但其实f(0) = max{prices[1],prices[2]...prices[n-1]}- prices[0]
        //而f(1) = max{prices[2]...prices[n-1]}- prices[1] 寻找最大值的过程中涉及重复的过程。
        //因此我们可以从后向前判断，并用一个变量去记录当前最大值。
        if(prices==null||prices.length==0)
            return 0;
        int currmax = prices[prices.length-1];
        //最大利润        
        int max = Integer.MIN_VALUE;
        for(int i=prices.length-2;i>=0;i--)
        {
            max = Math.max(currmax-prices[i],max);
            //时刻更新currmax，让currmax为从当前i（包括i）到其后的最大值，因为下一次判断的是f(i-1)。
            currmax = Math.max(currmax,prices[i]);
        }
        return max>0?max:0;
    }
}

26.打家劫舍 III

普通dfs

先明确子结构：以爷爷->两个儿子->四个孙子为例
从爷爷开始偷能偷的最多钱数为:
max = Math.max(爷爷偷的钱+四个孙子偷，两个儿子偷)
这里具体来说只有爷爷偷得钱是root.val，而四个孙子偷的钱，是以四个孙子为爷爷的情况下偷得最多钱，儿子同理，所以
max = Math.max(爷爷.val+rob(四个孙子)，rob（两个儿子）)

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
     /*先明确子结构：以爷爷->两个儿子->四个孙子为例
        从爷爷开始偷能偷的最多钱数为
        max = Math.max(爷爷偷的钱+四个孙子偷，两个儿子偷)
        这里具体来说只有爷爷偷得钱是root.val，而四个孙子偷的钱，是以四个孙子为爷爷的情况下偷得最多钱，儿子同理，所以
        max = Math.max(爷爷.val+rob(四个孙子)，rob（两个儿子）)
        */
    public int rob(TreeNode root) {
       
        if(root==null)
            return 0;
        int max = Integer.MIN_VALUE;
        int grandfather = root.val;
        if(root.left!=null)
        grandfather+=rob(root.left.left)+rob(root.left.right);
        if(root.right!=null)
        grandfather+=rob(root.right.left)+rob(root.right.right);
        int son = rob(root.left)+rob(root.right);
        max = Math.max(son,grandfather);
        return max;
    }
}

记忆化搜索

写一下重复的操作在哪里，假设二叉树为：

          		1
               / \
              2   3
             / \   \ 
            4   5   6
那么rob（1） =  Math.max((1.val+rob(4)+rob(5)+rob(6)),(rob(2)+rob(3)))
rob(2) = Math.max((2.val+0+0),(rob(4)+rob(5)))
rob(3) = Math.max((3.val+0+0),(rob(6)))
重复计算了rob(4),rob(5),rob(6)

记忆化搜索其实很简单，只需要申请一个数组来存储结果，注意这里是TreeNode我们需要用HashMap来存储结果。
代码如下：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    HashMap<TreeNode,Integer>map = new HashMap<>();
    public int rob(TreeNode root) {
       return find(root);
    }
    public int find(TreeNode root)
    {
        if(root==null)
            return 0;
        if(map.containsKey(root))
            return map.get(root);
        int max = Integer.MIN_VALUE;
        int grandfather = root.val;
        if(root.left!=null)
        grandfather+=rob(root.left.left)+rob(root.left.right);
        if(root.right!=null)
        grandfather+=rob(root.right.left)+rob(root.right.right);
        int son = rob(root.left)+rob(root.right);
        max = Math.max(son,grandfather);
        map.put(root,max);
        return max;
    }
}

dp解法：01背包

最终解法：考虑0,1背包问题
0:不偷当前节点，最大值为：偷取左子节点的最大值（不一定偷取左右节点，只是从左右节点考虑开始偷）+右子节点的最大值
1：偷当前节点，最大值为：不偷左子节点的最大值+不偷右子节点的最大值+当前节点的值
max = Math.max(0,1)

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public int rob(TreeNode root) {
        /*
        最终解法：考虑0,1背包问题
        0:不偷当前节点，最大值为：偷取左子节点的最大值（不一定偷取左右节点，只是从左右节点考虑开始偷）+右子节点的最大值
        1：偷当前节点，最大值为：不偷左子节点的最大值+不偷右子节点的最大值+当前节点的值
        max = Math.max(0,1)
        */
        int[]dp = new int[2];
        dp = find(root);
        return Math.max(dp[0],dp[1]);
    }
    public int[] find(TreeNode root)
    {
        int[]now = new int[2];
        if(root==null)
            return now;
        int[]rootleft = find(root.left);
        int[]rootright = find(root.right);
        /*这里是左子节点能偷到的最大值+右子节点能偷盗的最大值
        左子节点能偷到的最大值不一定要偷左子节点这个值
        比如左子节点为3的情况，不取3,1,3，1，而取4，5更大
                3
               / \
              4   5
             / \   \ 
            1   3   1
            
        */
        int no = Math.max(rootleft[1],rootleft[0])+Math.max(rootright[1],rootright[0]);
        int tou = root.val+rootleft[0]+rootright[0];
        now[0] = no;
        now[1] = tou;
        return now;
    }
}

27.编辑距离

思路

其实就是三步走
1.首先定义二维数组的含义：
dp[i][j]代表i长度的word1字符串转变为j长度的Word2需要的最小操作数
2.找出子结构
(1)当word1字符串的第i个字符与word2的第j个字符相同，就不需要转换。
dp[i][j] = dp[i-1][j-1]
(2)当word1字符串的第i个字符与word2的第j个字符不同，有三种操作。
1）删除一个字符(将i处字符删除，也就是用i-1长度的word1与j长度的word2比较)
dp[i][j] = dp[i-1][j]+1
2)插入一个字符（在i处字符后插入与word2[j]相同的字符，剩下就是i长度的word1与j-1长度的word2比较）
dp[i][j] = dp[i][j-1]+1
3）替换一个字符(i处字符替换为与j相同的字符，剩下比较i-1长度的word1与j-1长度的word2)
dp[i][j] = dp[i-1][j-1]+1
Max(上面三种情况)
3.初始情况：
只要i或者j为0，就全部替换为对方长度。

代码

class Solution {
    public int minDistance(String word1, String word2) {
        char[]word1Array = word1.toCharArray();
        char[]word2Array = word2.toCharArray();
        int[][]dp = new int[word1Array.length+1][word2Array.length+1];
        //当word2长度为0时，就把word1的全部删除即可
        for(int i=1;i<=word1Array.length;i++)
        {
            dp[i][0] = i;
        }
        //当word1长度为0时，就插入所有word2的字符即可
        for(int j=1;j<=word2Array.length;j++)
        {
            dp[0][j] = j;
        }
        for(int i=1;i<=word1Array.length;i++)
        {
            for(int j=1;j<=word2Array.length;j++)
            {
                //第i个字符代表的是下标为i-1
                if(word1Array[i-1]==word2Array[j-1])
                    dp[i][j] = dp[i-1][j-1];
                else{
                    //在i处插入一个字符
                    int insert = dp[i][j-1]+1;
                    //替换一个字符
                    int change = dp[i-1][j-1]+1;
                    //删除一个字符
                    int delte = dp[i-1][j]+1;
                    dp[i][j] = Math.min(Math.min(insert,change),delte);
                }
            }
        }
        return dp[word1Array.length][word2Array.length];
    }
}

28.分割等和子集

思路

首先要明白这个题是一道0-1背包问题。如何抽象成0-1背包问题就看个人的水平。所以算法高手就是能把实际问题抽象成算法问题。可以把这个问题抽象成从N个数中随便选取，尝试填充满sum/2的背包。
因此转移方程如下：

F(n,c)考虑将n个物品填满容量为C的背包
        F（i，c） = F(i-1,c)||F(i-1,c-w (i))
        时间复杂度：O（n*sum/2） = O(n*sum)

递归+记忆化搜索

我们很容易就能写出一版递归的代码。有一些注意条件（1）sum值不能是奇数，否则直接返回false。
递归终止条件：
（1）length长度为1时，相当于判断nums[0]是否等于当前允许容量C，这个也是相当于初始条件。 (2)length<0时，直接返回false
（3）如果容量为0，说明之前已经找到了结果，那么可以直接退出了（返回true）。

class Solution {
    public boolean canPartition(int[] nums) {
        /*背包问题，考虑在n个物品中选出一定物品，填满sum/2的背包。
        F(n,c)考虑将n个物品填满容量为C的背包
        F（i，c） = F(i-1,c)||F(i-1,c-w (i))
        时间复杂度：O（n*sum/2） = O(n*sum)
        */
        int sum = 0;
        for(int num:nums)
        {
            sum+=num;
        }
        //比如1235
        if(sum%2!=0)
            return false;
        return canfind(nums,nums.length-1,sum/2);
    }
    public boolean canfind(int[]nums,int length,int C)
    {
        //初始值(长度为1时，就判断这个值是否与C相等)
        if(length==0)
            return nums[length]==C;
        if(length<0)
            return false;
        //已经填满了
        if(C==0){
            System.out.println(length);
            return true;
        }
        //正常返回值：1.不要nums[length]这个值，就在[0,length-1]内去判断是否能满足C
        //2.要nums[length]这个值，就在[0,length-1]内去判断能否满足C-nums[length]
        return canfind(nums,length-1,C)||canfind(nums,length-1,C-nums[length]);
    }
}

如果运行的话会出现超时，好的，我们改为记忆化搜索咯。

class Solution {
    int[][]memo;
    public boolean canPartition(int[] nums) {
        /*背包问题，考虑在n个物品中选出一定物品，填满sum/2的背包。
        F(n,c)考虑将n个物品填满容量为C的背包
        F（i，c） = F(i-1,c)||F(i-1,c-w (i))
        时间复杂度：O（n*sum/2） = O(n*sum)
        */
        int sum = 0;
        for(int num:nums)
        {
            sum+=num;
        }
        //比如1235
        if(sum%2!=0)
            return false;
        memo = new int[nums.length][sum/2+1];
        return canfind(nums,nums.length-1,sum/2);
    }
    public boolean canfind(int[]nums,int length,int C)
    {
        //初始值(长度为1时，就判断这个值是否与C相等)
        if(length==0)
            return nums[length]==C;
        if(length<0)
            return false;
        //已经填满了
        if(C==0){
            System.out.println(length);
            return true;
        }
        if(memo[length][C]!=0)
            return memo[length][C]==1?true:false;
        //正常返回值：1.不要nums[length]这个值，就在[0,length-1]内去判断是否能满足C
        //2.要nums[length]这个值，就在[0,length-1]内去判断能否满足C-nums[length]
       boolean flag = canfind(nums,length-1,C)||canfind(nums,length-1,C-nums[length]);
       if(flag==true)
        memo[length][C] = 1;
        else
        memo[length][C] = 2;
        return flag;
    }
}

又出现错误用例

这时发现我们没有限制容量小于0这个条件，如果小于0，我们也要返回false。最终记忆化搜索代码如下：

class Solution {
    int[][]memo;
    public boolean canPartition(int[] nums) {
        /*背包问题，考虑在n个物品中选出一定物品，填满sum/2的背包。
        F(n,c)考虑将n个物品填满容量为C的背包
        F（i，c） = F(i-1,c)||F(i-1,c-w (i))
        时间复杂度：O（n*sum/2） = O(n*sum)
        */
        int sum = 0;
        for(int num:nums)
        {
            sum+=num;
        }
        //比如1235
        if(sum%2!=0)
            return false;
        memo = new int[nums.length][sum/2+1];
        return canfind(nums,nums.length-1,sum/2);
    }
    public boolean canfind(int[]nums,int length,int C)
    {
        //初始值(长度为1时，就判断这个值是否与C相等)
        if(length==0)
            return nums[length]==C;
        if(length<0||C<0)
            return false;
        //已经填满了
        if(C==0){
            System.out.println(length);
            return true;
        }
        if(memo[length][C]!=0)
            return memo[length][C]==1?true:false;
        //正常返回值：1.不要nums[length]这个值，就在[0,length-1]内去判断是否能满足C
        //2.要nums[length]这个值，就在[0,length-1]内去判断能否满足C-nums[length]
       boolean flag = canfind(nums,length-1,C)||canfind(nums,length-1,C-nums[length]);
       if(flag==true)
        memo[length][C] = 1;
        else
        memo[length][C] = 2;
        return flag;
    }
}

其实这里还可以继续优化，设立一个flag，当C=0时，flag赋值true，在每次进入canfind循环先判断flag是否为true，如果为true，直接返回true即可，无需继续计算。

动态规划

class Solution {
    public boolean canPartition(int[] nums) {
        int sum= 0;
        for(int num:nums)
            sum+=num;
        if(sum%2!=0)
            return false;
        int N = nums.length;
        int C = sum/2;
        //dp[i][j]代表nums[0-i]是否可以填充容量为j的背包
        boolean[][]dp = new boolean[N][C+1];
        for(int j=0;j<=C;j++)
        {
            if(nums[0]==j)
                dp[0][j] = true;
        }
        for(int i=1;i<N;i++)
        {
            for(int j=1;j<=C;j++)
            {

                dp[i][j] = dp[i-1][j];
                if(j>=nums[i])
                dp[i][j] =dp[i][j]||dp[i-1][j-nums[i]];
            }
        }
        return dp[N-1][C];
    }
}

29.一和零

思路

还是要找到我们的状态方程代表什么。还是一个0-1背包问题嘛，只不过容量变成了两个，一个容量是0的个数，一个容量是1的个数。因此可以如下定义。

定义f(i,m,n) 为取前i+1个数，且在m个0与n个1的情况下，所能拼出的最大字符串数。
f(i,m,n) = f(i-1,m,n)+f(i-1,m-strs[i](0),n-strs[i](1))+1

注意什么情况可以将当前i的存入呢，当前剩余的m>=strs[i]中0的个数同时n>=strs[i]中1的个数。

普通递归算法

让我们先写一个超时的普通递归。注意终止递归的条件：
1.i<0,没有物品了
2.m0&&n0，没有容量了
所能拼出的字符串数都应该为0。

class Solution {
    public int findMaxForm(String[] strs, int m, int n) {
        /*
        定义f(i,m,n) 为取前i+1个数，且在m个0与n个1的情况下，所能拼出的最大字符串数。
        f(i,m,n) = f(i-1,m,n)+f(i-1,m-strs[i](0),n-strs[i](1))+1
        */
        return find(strs,strs.length-1,m,n);
    }
    public int find(String[]strs,int i,int m,int n)
    {
        //递归终止条件
        if(i<0)
            return 0;
        //没有容量了，直接返回0即可
        if(m==0&&n==0)
            return 0;
        //常规
        String nows = strs[i];
        int now0 = 0;
        int now1 = 0;
        for(int t = 0;t<nows.length();t++)
        {
            if(nows.charAt(t)=='0')
                now0++;
            else
                now1++;
        }
        int qu = 0;
        if(m>=now0&&n>=now1)
            qu = find(strs,i-1,m-now0,n-now1)+1;
        int buqu = find(strs,i-1,m,n);
        return Math.max(qu,buqu);
    }
}

看到超时很开心。

记忆化搜索

创建一个三维数组用来存储我们的结果。注意一个好习惯，要给记忆数组赋初值-1。

class Solution {
    int[][][]memo;
    public int findMaxForm(String[] strs, int m, int n) {
        /*
        定义f(i,m,n) 为取前i+1个数，且在m个0与n个1的情况下，所能拼出的最大字符串数。
        f(i,m,n) = f(i-1,m,n)+f(i-1,m-strs[i](0),n-strs[i](1))+1
        */
        memo = new int[strs.length][m+1][n+1];
        for(int i=0;i<strs.length;i++)
        {
            for(int j=0;j<m+1;j++)
            {
                Arrays.fill(memo[i][j],-1);
            }
        }
        return find(strs,strs.length-1,m,n);
    }
    public int find(String[]strs,int i,int m,int n)
    {
        //递归终止条件
        if(i<0)
            return 0;
        //没有容量了，直接返回0即可
        if(m==0&&n==0)
            return 0;
        if(memo[i][m][n]!=-1)
            return memo[i][m][n];
        //常规
        String nows = strs[i];
        int now0 = 0;
        int now1 = 0;
        for(int t = 0;t<nows.length();t++)
        {
            if(nows.charAt(t)=='0')
                now0++;
            else
                now1++;
        }
        int qu = 0;
        if(m>=now0&&n>=now1)
            qu = find(strs,i-1,m-now0,n-now1)+1;
        int buqu = find(strs,i-1,m,n);
        memo[i][m][n] = Math.max(qu,buqu);
        return memo[i][m][n];
    }
}

动态规划

这里注意两个事情：
1.初始值，当i=0时，其实就判断zero和one是否大于等于strs[i]中0和1的个数，如果满足条件memo[i][zero][one]就赋值1。

 if(nowone<=one&&nowzero<=zero){
		if(i>0)
			memo[i][zero][one] = Math.max(memo[i][zero][one],memo[i-1][zero-nowzero][one-nowone]+1);
		else
		//初始值
			memo[i][zero][one] = 1;
}

2.容量要从0开始，通常都考虑容量选取1开始，而这里有两个容量，当一个容量为0，另一个不为零，是有可能能组成strs中的字符串的。
详细代码

class Solution {
    int[][][]memo;
    public int findMaxForm(String[] strs, int m, int n) {
        /*
        定义f(i,m,n) 为取前i+1个数，且在m个0与n个1的情况下，所能拼出的最大字符串数。
        f(i,m,n) = f(i-1,m,n)+f(i-1,m-strs[i](0),n-strs[i](1))+1
        */
        memo = new int[strs.length][m+1][n+1];
        for(int i=0;i<strs.length;i++)
        {
            String nowString = strs[i];
            int nowzero = 0;
            int nowone = 0;
            for(int k = 0;k<nowString.length();k++)
            {
                char c = nowString.charAt(k);
                if(c=='0')
                    nowzero++;
                else
                    nowone++;
            }
            //这里应该是从两个都为0开始，因为有可能一个为0，一个为1。比如字符串为“1”，只需要1个one,和0个0
            //也就是说循环必须包括一个为0，一个为从0一直到最大数目（比如，zero为0，one从0到n）
            for(int zero = 0;zero<=m;zero++)
            {
                for(int one = 0;one<=n;one++)
                {
                    if(i>0)
                        memo[i][zero][one] = memo[i-1][zero][one];
                    if(nowone<=one&&nowzero<=zero)
                        {
                        //System.out.println(i+" "+zero+" "+one+" ");
                        if(i>0)
                            memo[i][zero][one] = Math.max(memo[i][zero][one],memo[i-1][zero-nowzero][one-nowone]+1);
                        else
                            //初始值
                            memo[i][zero][one] = 1;
                        }
                }
            }
        }
    
        return memo[strs.length-1][m][n];
        
    }
    
}

优化空间的动态规划

注意背包问题或者说动态规划理论上都可以降维，但是降维之后一定要注意一点：

注意这里不能从小到大去找，和之前的背包问题优化相似，要从后向前找。
假如从前向后找，会导致当前的memo[zero][one]已经变成了下一行的值，那么我之后再需要用memo[zero][one]就不是上一行的
memo[zero][one]了

完整代码：

class Solution {
    int[][]memo;
    public int findMaxForm(String[] strs, int m, int n) {
        /*
        定义f(i,m,n) 为取前i+1个数，且在m个0与n个1的情况下，所能拼出的最大字符串数。
        f(i,m,n) = f(i-1,m,n)+f(i-1,m-strs[i](0),n-strs[i](1))+1
        */
        memo = new int[m+1][n+1];
        for(int i=0;i<strs.length;i++)
        {
            String nowString = strs[i];
            int nowzero = 0;
            int nowone = 0;
            for(int k = 0;k<nowString.length();k++)
            {
                char c = nowString.charAt(k);
                if(c=='0')
                    nowzero++;
                else
                    nowone++;
            }
            //注意这里不能从小到大去找，和之前的背包问题优化相似，要从后向前找。
            //假如从前向后找，会导致当前的memo[zero][one]已经变成了下一行的值，那么我之后再需要用memo[zero][one]就不是上一行的
            //memo[zero][one]了
            for(int zero = m;zero>=0;zero--)
            {
                for(int one = n;one>=0;one--)
                {
                    if(nowone<=one&&nowzero<=zero)
                        {
                        //
                        //System.out.println(i+" "+zero+" "+one+" ");
                        if(i>0)
                            memo[zero][one] = Math.max(memo[zero][one],memo[zero-nowzero][one-nowone]+1);
                        else
                            //初始值
                            memo[zero][one] = 1;
                        }
                }
            }
        }
    
        return memo[m][n];
        
    }
    
}

30.单词拆分

思路

这个题很明显是一个完全背包问题，

常规思路考虑：
f(i,c)代表wordDict取[0,i]是否可以组成s。但这种思路显而易见很复杂，因为s也要是从0-s.length,
我们可以换一种思路。
f(i)代表s长度为i时，可否由wordDict组成
判断过程也很简单，考虑是否能组成，可以将这部分拆分成两段:0-k看能不能由wordDict组成，k-i部分看能不能由wordDict组成
k由1到i-1，同时当我们求f(i)时，已经知道了f(i-1)...f(1)的值，因此只要判断k-i部分能不能由wordDict组成即可。
而k-i部分能不能由wordDict组成，只需要看wordDict中是否包含k-i部分的单词。
f(i) = f(1)&&wordDict.cotains(s(1,i)||f(2)&&wordDict.contains(s(2,i))||...

其实可以看到这道题的思路和之前的零钱最节省时间的方法类似，那道题也是定义f（i）为钱为i时，能否由coins凑齐，

f（i） = f(i-coins[0])||f(i-coins[1])||f(i-coins[2])...

当然那道题求得是最小次数，上面的方程是假设判断能否凑齐。

动态规划代码

class Solution {
    public boolean wordBreak(String s, List<String> wordDict) {
        boolean[]dp = new boolean[s.length()+1];
        //长度为0肯定可以组成
        dp[0] = true;
        for(int i=1;i<=s.length();i++)
        {
            //本身是否就直接在wordDict中
            dp[i] = wordDict.contains(s.substring(0,i));
            for(int j=1;j<=i-1;j++)
            {
                if(dp[j]&&wordDict.contains(s.substring(j,i)))
                   {
                        dp[i] = true;
                        break;
                   }
            }
        }
        return dp[s.length()];
        
    }
}

31.目标和

思路

很明显是一个变种的0-1背包问题
怎么变种呢，正常思路是取或者不取，而这个题是取-或者取+号，因此我们可以得到这个关系式。同时注意S可以取负数。

如果当前取-号，那么就是从[0,i-1]去凑S+nums[i]；如果取+号，那么就是从[0,i-1]去凑S-nums[i]
f(i,s) = f(i-1,s+nums[i])+f(i-1,s-nums[i])

还是先写递归看看

递归思路

class Solution {
    public int findTargetSumWays(int[] nums, int S) {
        /* 0-1背包问题，只是这里是取-和取+,f(i,s)代表前i+1能凑成s的个数
        如果当前取-号，那么就是从[0,i-1]去凑S+nums[i],如果取+号，那么就是[0,i-1]去凑S-nums[i]
        f(i,s) = f(i-1,s+nums[i])+f(i-1,s-nums[i])
        */
        return find(nums,nums.length-1,S);
    }
    public int find(int[]nums,int i,int s)
    {
        if(i<0)
            return 0;
        if(i==0){
            //正负都可以
            if(nums[i]==Math.abs(s))
                return 1;
            else 
                return 0;
        }
        //常规
        int result = find(nums,i-1,s+nums[i])+find(nums,i-1,s-nums[i]);
        //System.out.println("result= "+result+","+"i: "+i+",s: "+s);
        return result;
   }
}

这里其实有个致命的问题，如果nums[0]=0,且s为0的话，不应该返回1，而应该返回2。也就是说取+或者-都可以是0。
当示例为[0,0,0,0,0,0,0,0,1],1时，返回的就是128，就是因为没有考虑当nums[0] = 0且s=0的情况应该为2。
因此，正确代码：

class Solution {
    public int findTargetSumWays(int[] nums, int S) {
        /* 0-1背包问题，只是这里是取-和取+,f(i,s)代表前i+1能凑成s的个数
        如果当前取-号，那么就是从[0,i-1]去凑S+nums[i],如果取+号，那么就是[0,i-1]去凑S-nums[i]
        f(i,s) = f(i-1,s+nums[i])+f(i-1,s-nums[i])
        */
        return find(nums,nums.length-1,S);
    }
    public int find(int[]nums,int i,int s)
    {
        if(i<0)
            return 0;
       
        if(i==0){
            //正负都可以
            int result = 0;
            if(nums[0]==Math.abs(s))
            {  
                result++;
                //防止nums[0]为0且等于s
                if(nums[0]==0)
                    result++;
                return result;
                }
            else 
                return result;
        }
        //常规
        int result = find(nums,i-1,s+nums[i])+find(nums,i-1,s-nums[i]);
        if(i==0)
            System.out.println("result= "+result+","+"i: "+i+",s: "+s);
        return result;
   }
}

效果一般，不过也通过了。

动态规划

首先和背包问题不同的是，可能是从容量0到最大容量（或者钱数从0到最大比如零钱兑换之类的）循环，这里应该是从-sum值到sum值循环，因为这些值全取减号就是-sum。换句话说就是需要知道dp[i][-sum]，也需要知道dp[i][sum]。
其实核心点在于要将范围转变一下，由[-sum,sum]转变成[0,2sum+1]。

class Solution {
    public int findTargetSumWays(int[] nums, int S) {
        /* 0-1背包问题，只是这里是取-和取+,f(i,s)代表前i+1能凑成s的个数
        如果当前取-号，那么就是从[0,i-1]去凑S+nums[i],如果取+号，那么就是[0,i-1]去凑S-nums[i]
        f(i,s) = f(i-1,s+nums[i])+f(i-1,s-nums[i])
        直接写dp解法吧
        因为s是从[-sum,sum]，因此要将这个范围转化为[0,2sum],0对应的是-sum。sum对应0
        */
       int sum = 0;
       for(int num:nums)
        sum+=num;
        if(S<-sum||S>sum)
            return 0;
        int[][]dp = new int[nums.length][sum*2+1];
        //赋初值
        dp[0][nums[0]+sum] = 1;
        //防止nums[0]为0
        dp[0][sum-nums[0]] += 1;
        for(int  i=1;i<nums.length;i++)
        {
            for(int s = 0;s<=2*sum;s++)
            {
                //不能超过上限
                if(s+nums[i]<=2*sum)
                    dp[i][s] += dp[i-1][s+nums[i]];
                //不能超过下限
                if(s-nums[i]>=0)
                    dp[i][s] += dp[i-1][s-nums[i]];
            }
        }
        
        return dp[nums.length-1][S+sum];
    }
    
}

效果还可以。

32.零钱兑换 II

思路

其实就是个完全背包问题，要注意的就是我们将dp数组的定义。这里还要注意一点，不能把钱放在外层，coin放在内层循环，会重复加和的。

代码

class Solution {
    public int change(int amount, int[] coins) {
        /*
        完全背包问题
        dp[i][money]代表前i+1个数，能组成money的个数
        dp[i][money] = sum(dp[i-1][money]+dp[i-1][money-1*coins[i]]+dp[i-1][money-2*[coins[i]]])
        优化解法：
        默认当前只取一个coins[i]，那么剩余的部分就变成了money-coins[i]，这部分在前面考虑过了（可能前面这部分也有多个coins[i]）
        dp[i][money]+=dp[i][money-i*coins[i]]
        */
        if(amount==0)
            return 1;
        if(coins==null||coins.length==0)
            return 0;
        int[][]dp = new int[coins.length][amount+1];
        for(int j=1;j<=amount;j++)
        {
            if(j%coins[0]==0)
                dp[0][j]=1;
        }
        for(int i=0;i<coins.length;i++)
        {
            //留着给之后如果money=coins[i]的情况
            dp[i][0] = 1;
        }
        //对应每个i去判断。
        for(int i=1;i<coins.length;i++)
        {
            for(int j=1;j<=amount;j++)
            {
            	//不取
                dp[i][j] = dp[i-1][j];
                //可以取一个,剩余部分就是j-coins[i](他们的组合数就是1个coins[i]固定，剩余为前i个数如何组成j-coins[i])
                if(j>=coins[i])
                    dp[i][j]+=dp[i][j-coins[i]];
            }
        }
        return dp[coins.length-1][amount];
    }
}

33.抛掷硬币

思路

其实我觉得这个题是个0-1背包问题，我们可以将问题抽象为：

f(i,target)：抛掷前i+1个硬币，正面朝上的硬币数等于target的概率
当前投出target可以是（1）当前没投出正面，前i个投出target（2）当前投出正面，前i个投出target-1
f(i,target) = f(i-1,target-1)*prob[i]+f(i-1,target)*(1-prob[i])

记忆化搜索

老规矩，先写自顶向下，这里格外要注意的就是不能出现dfs（1,3），因为现在prob中就两枚硬币（i=0,1），肯定不能出现3个正面向上的硬币。

class Solution {
    double[][]memo;
    public double probabilityOfHeads(double[] prob, int target) {
        //f(i,target)抛掷前i个硬币，正面超上的硬币数等于target的概率
        //当前投出target可以是（1）当前没投出正面，前i-1个投出target（2）当前投出正面，前i-1个投出target-1
        //f(i,target) = f(i-1,target-1)*prob[i]+f(i-1,target)*(1-prob[i])
        memo = new double[prob.length][target+1];
        for(int i=0;i<prob.length;i++)
        {
            Arrays.fill(memo[i],-1);
        }
        return dfs(prob,prob.length-1,target);
    }
    public double dfs(double[] prob, int index,int target)
    {
        //终止条件
        //（1）target最大只能为0（2）当前prob中硬币的个数小于target值，肯定摇不出target
         if(target<0||index+1<target)
            return 0;
        if(memo[index][target]!=-1)
            return memo[index][target];
        //初始条件
        if(index==0){
            if(target==1)
                return prob[0];
            else
                return 1-prob[0];
        }
        //常规
        memo[index][target] = dfs(prob,index-1,target-1)*prob[index]+dfs(prob,index-1,target)*(1-prob[index]);
        return memo[index][target];
    }
}

动态规划

class Solution {
    public double probabilityOfHeads(double[] prob, int target) {
        /*
        dp[i,target]代表抛掷前i个硬币，正面超上的硬币数等于target的概率
        当前投出target可以是（1）当前没投出正面，前i-1个投出target（2）当前投出正面，前i-1个投出target-1
        dp[i,target] = dp[i-1,target-1]*prob[i]+dp[i-1,target]*(1-prob[i])
        */
        double result = 1;
        //如果target=0
        if(target==0){ 
            for(double coin:prob)
                result = result*(1-coin);
            return result;
        }
        int N = prob.length;
        double [][]dp = new double[N][target+1];
        dp[0][0] = 1-prob[0];
        dp[0][1] = prob[0];
        for(int i=1;i<prob.length;i++)
        {
            for(int j=0;j<=target;j++)
            {
                //不能让当前prob中可用的硬币数（i+1）小于j（正面超上的硬币数）
                if(i+1<j)
                    break;
                dp[i][j] = dp[i-1][j]*(1-prob[i]);
                if(j-1>=0)
                dp[i][j]+=dp[i-1][j-1]*prob[i];
            }
        }
        return dp[N-1][target];
    }
}

优化时间的动态规划

可以看出转移方程为

 dp[i,target] = dp[i-1,target-1]*prob[i]+dp[i-1,target]*(1-prob[i])

第i行的结果只与第i-1行的数值有关系，因此可以只使用一维的数组来存储数值。

class Solution {
    public double probabilityOfHeads(double[] prob, int target) {
        /*
        dp[i,target]代表抛掷前i个硬币，正面超上的硬币数等于target的概率
        当前投出target可以是（1）当前没投出正面，前i-1个投出target（2）当前投出正面，前i-1个投出target-1
        dp[i,target] = dp[i-1,target-1]*prob[i]+dp[i-1,target]*(1-prob[i])
        */
        double result = 1;
        //如果target=0
        if(target==0){ 
            for(double coin:prob)
                result = result*(1-coin);
            return result;
        }
        int N = prob.length;
        double []dp = new double[target+1];
        dp[0] = 1-prob[0];
        dp[1] = prob[0];
        for(int i=1;i<prob.length;i++)
        {
            for(int j=target;j>=0;j--)
            {
                if(j>i+1)
                    continue;
                dp[j] = dp[j]*(1-prob[i]);
                if(j-1>=0)
                dp[j]+=dp[j-1]*prob[i];
            }
        }
        return dp[target];
    }
}

34.最长上升子序列

思路

这是一种新的题型，最长上升子序列问题。这里要注意观察题目，需要确定一些条件。
1.子序列还是连续的子序列。2.自身是不是上升子序列。
这里采用子序列可以让序列中的元素不需要连续，自身就是一个上升子序列。
接下来要考虑如何转换成动态规划问题。

LIS（i）表示以第i个数字为结尾的最长上升子序列的长度
这里一定要选择第i个数字
j从0，i-1去判断，如果nums[i]大于nums[j],就可以将nums[i]与nums[j]连接起来,就是1+LIS(j)
LIS(i) = Max(if(nums[i]>nums[j])LIS(j)+1),j:[0,i-1]

动态规划

既然转移方程已经写好，就可以直接撸代码了，需要注意的就是初始条件的赋值，最后将以每个数字为结尾的dp数组写好后，还需要遍历寻找最大值。

class Solution {
    public int lengthOfLIS(int[] nums) {
        /*
        LIS（i）表示以第i个数字为结尾的最长上升子序列的长度
        这里一定要选择第i个数字
        j从0，i-1去判断，如果nums[i]大于nums[j],就可以将nums[i]与nums[j]连接起来,就是1+LIS(j)
        LIS(i) = Max(if(nums[i]>nums[j])LIS(j)+1),j:[0,i-1]
        */
        //防止数组为空
        if(nums.length==0||nums==null)
            return 0;
        int[]dp = new int[nums.length];
        //自己就是一个上升子序列(所以初值可以为1)
        dp[0] = 1;
        for(int i=1;i<nums.length;i++)
        {
            dp[i] = 1;
            for(int j=0;j<i;j++)
            {
                if(nums[i]>nums[j])
                    dp[i]  = Math.max(dp[i],dp[j]+1);
            }
        }
        int max = 1;
        for(int d:dp)
        {
            if(d>max)
                max = d;
        }
        return max;
    }
}

35.摆动序列

思路

与上一道题类似，区别在于，摆动序列的定义，以[1,7,4,9,2,5]为例，这就是一个摆动序列，因为差值 (6,-3,5,-7,3) 是正负交替出现的。
我们可以同样定义dp[i]为代表取i为结尾能取到的最长摆动序列长度。我们需要注意以下几点。
（1）题中有条件少于两个元素的序列也是摆动序列，因此只有一个元素的话也是摆动序列。
（2）如果取当前i作为摆动序列的尾部，它有两种可能：
1.比nums[j]大，这样由nums[j]到nums[i]组成升序，如果可以组成摆动序列的话，前面的值和nums[j]就需要是降序关系
2.比nums[j]小，这样由nums[j]到nums[i]组成降序，如果可以组成摆动序列的话，前面的值和nums[j]就需要是升序关系
由此可知，我们不能只定义一维数组，我们需要定义二维数组，状态方程如下：

		想取dp[i][0]代表以i为结尾且i-1到i为升,dp[i][1]代表以i为结尾且i-1到i为降
        当前nums[i]大于nums[j]，则可以取从j到i上升，因此可以取dp[j][i]+1，因此之前的值与j需要是下降关系所以取的是dp[j][1]
        dp[i][0] = Math.max(if(nums[i]>nums[j])dp[j][1]+1),j:[0,i-1]
        与上面同理
        dp[i][1] = Math.max(if(nums[i]<nums[j])dp[j][0]+1),j:[0,i-1]

最后在遍历dp数组找到最大值。

代码

class Solution {
    public int wiggleMaxLength(int[] nums) {
        /*动态规划
        dp[i]代表取i以结尾能取到的最长摆动序列的长度
        想取dp[i][0]代表以i为结尾且i-1到i为升,dp[i][1]代表以i为结尾且i-1到i为降
        当前nums[i]大于nums[j]，则可以取从j到i上升，因此可以取dp[j][i]+1，因为j需要与之前的值是下降关系所以取的是dp[j][1]
        dp[i][0] = Math.max(if(nums[i]>nums[j])dp[j][1]+1),j:[0,i-1]
        与上面同理
        dp[i][1] = Math.max(if(nums[i]
        if(nums==null||nums.length==0)
            return 0;
        if(nums.length<2)
            return 1;
        int[][]dp = new int[nums.length][2];
        dp[0][0] = 1;
        dp[0][1] = 1;
        for(int i=1;i<nums.length;i++)
        {
            dp[i][0] = 1;
            dp[i][1] = 1;
            for(int j=0;j<i;j++)
            {
                if(nums[i]>nums[j])
                    dp[i][0] = Math.max(dp[i][0],dp[j][1]+1);
                else if(nums[i]<nums[j])
                    dp[i][1] = Math.max(dp[i][1],dp[j][0]+1);
            }   
        }
        int max =1;
        for(int i=0;i<nums.length;i++)
        {
            int nowmax = Math.max(dp[i][0],dp[i][1]);
            max = Math.max(max,nowmax);
        }
        return max;
    }
}

36.最长公共子序列

这种问题叫做最长公共子序列问题（LCS问题），如果使用动态规划我们需要定义一个二维的数组来存储信息。还是老规矩，我们先写下转移方程和最优子结构。

			f(i,j)代表text1（0,i）与text2(0,j)之间最长的公共子序列
            f(i,j) = 
            相等就都往前退一位
            if(text1(i)==text2(j)) f(i-1,j-1)+1
            //i处如果与j处不相等，那么可以删除字符，删除i或者删除j
            else 
            max(f(i-1,j),f(i,j-1))

既然很清晰的话，我们就先写一下递归的代码

自顶向下（记忆化搜索）

递归结束条件：如果i或者j小于0，那么肯定就没有公共子序列了。没有多余其他判断结束条件了。我们可能会考虑当i和j都等于0的时候需不需要单独判断，这里是不需要的，因为当i和j都等于0的时候，也会进入常规判断。

class Solution {
    int[][]memo;
    public int longestCommonSubsequence(String text1, String text2) {
        /*f(i,j)代表text1（0,i）与text2(0,j)之间最长的公共子序列
            f(i,j) = 
            相等就都往前退一位
            if(text1(i)==text2(j)) f(i-1,j-1)+1
            //i处如果与j处不想等，那么可以删除字符，删除i或者删除j
            else 
            max(f(i-1,j),f(i,j-1))
        */
        memo = new int[text1.length()][text2.length()];
        for(int i=0;i<text1.length();i++)
            Arrays.fill(memo[i],-1);
        return dfs(text1,text2,text1.length()-1,text2.length()-1);
    }
    public int dfs(String text1,String text2,int i,int j){
        //有一个为0了，就不有最长公共子序列了
        if(i<0||j<0)
            return 0;
        if(memo[i][j]!=-1)
            return memo[i][j];
        int now = 0;
        //常规
        if(text1.charAt(i)==text2.charAt(j))
        {
            now =  1+dfs(text1,text2,i-1,j-1);
        }else{
            now = Math.max(dfs(text1, text2, i-1, j),dfs(text1,text2,i,j-1));
        }
        memo[i][j] = now;
        return memo[i][j];
    }
}

自底向上：动态规划

注意这里还是不需要有初始条件，只不过在判断当前i和j指向的字符相等后，要判断i和j是否都大于0，都大于0才可以使用dp[i][j]+1，否则就赋值为1。如果判断当前i和j指向的字符不相等，也需要判断i和j是否满足条件以去掉当前i或当前j位置的字符。

class Solution {
    public int longestCommonSubsequence(String text1, String text2) {
         /*dp(i,j)代表text1（0,i）与text2(0,j)之间最长的公共子序列
            dp(i,j) = 
            相等就都往前退一位
            if(text1(i)==text2(j)) dp(i-1,j-1)+1
            //i处如果与j处不想等，那么可以删除字符，删除i或者删除j
            else 
            max(dp(i-1,j),dp(i,j-1))
        */
        if(text1.length()==0||text2.length()==0)
            return 0;
        int[][]dp = new int[text1.length()][text2.length()];
        for(int i=0;i<text1.length();i++)
        {
            for(int j=0;j<text2.length();j++)
            {
                if(text1.charAt(i)==text2.charAt(j)){
                    if(i>0&&j>0)
                        dp[i][j] = dp[i-1][j-1]+1;
                    else
                        dp[i][j] = 1;
                }
                //去掉i的字符
                else {
                    if(i>=1)
                        dp[i][j] = Math.max(dp[i][j],dp[i-1][j]);
                    if(j>=1)
                        dp[i][j] = Math.max(dp[i][j],dp[i][j-1]);
                }
            }
        }
        return dp[text1.length()-1][text2.length()-1];
    }
}