通过时间序列分析预测未来广州的空气质量指数变化

摘要

文章通过研究收集到2014-2019五年间每月广州平均空气质量指数 （AQI） ，建立多个时间序列模型进行比较，得到最适合的模型预测广州未来空气质量指数。

引言

环境保护与空气质量一直是政府与民众关注的社会热点问题，2019年9月燃烧至今的澳洲山火火势仍未得到控制，山火产生的有毒烟雾正随着季风被吹向全球每个角落；自改革开放以来，中国经济增长迅速，工业化程度与人均汽车拥有量都在稳步提高，以广州为例，2017 年 GDP 总量达 2.15万亿， 2018 年 GDP 总量达 2.3 万亿元，年增长率达 6.9%。 2017 年机动车产量超 310 万辆，位居全国城市之首； 工业规模与机动车数量的不断扩大，广州的空气质量饱受社会关注。
近年来许多学者对于空气质量指数都有独到的研究与分析，陈焕盛【1】 对 2010 年广州气象要素和 PM10 日均浓度进行气象场、排放源的空间对比、时间序列对比、散点分析、统计分析，较为全面地判断气候条件对于空气质量的影响。林植林【2】基于 ARIMA 模型对 2014年广州市日空气质量指数进行预测，其他文献则对空气质量预测标准的合理性进行介绍。
文章使用数据来源为https://www.aqistudy.cn/historydata/monthdata.php?city=%E5%B9%BF%E5%B7%9E（PM2.5历史数据网），收集广州2014-2019五年间每月的平均空气质量指数，对数据进行时间序列分析，通过其 AIC 值、 BIC 值等参数检验计算，提出广州空气质量指数预测模型，预测未来六个月的空气质量指数。

研究思路

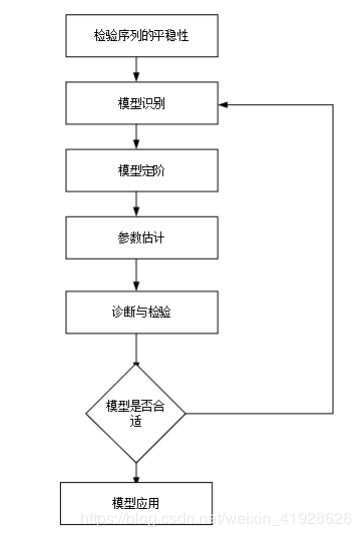
收集广州空气质量指数数据，对数据进行时间序列建模，定性与定量分析相结合，研究思路流程图如下

图1： 广州空气质量指数研究思路流程图

文章获取广州市 2014-2019五年间每月平均空气质量指数，利用 Stata15 分析软件构建广州空气质量指数的时间序列分析模型，首先进行数据平稳性检验，判断数据平稳后接着识别模型等等步骤，最后通过理论与实际指数的比较，预测并分析未来广州六个月空气质量指数。

空气质量指数平稳性分析

图2：时间序列图

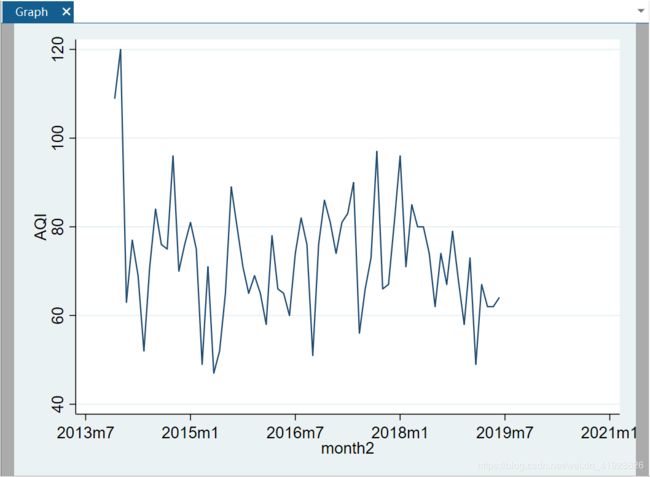
可以看出，AQI值在70附近剧烈波动，为证明时间序列图的平稳性，对时间序列进行单位根（ADF）检验。

ADF检验表

Dickey-Fuller test for unit root                   Number of obs   =        66

                               ---------- Interpolated Dickey-Fuller ---------
                  Test         1% Critical       5% Critical      10% Critical
               Statistic           Value             Value             Value
------------------------------------------------------------------------------
 Z(t)             -6.619            -3.558            -2.917            -2.594
------------------------------------------------------------------------------
MacKinnon approximate p-value for Z(t) = 0.0000

ADF 检验统计量值-6.619，小于 1%显著性水平下的临界值-3.558，拒绝存在单位根的零假设，说明时间序列是平稳的，无单位根存在。

图3：自相关图

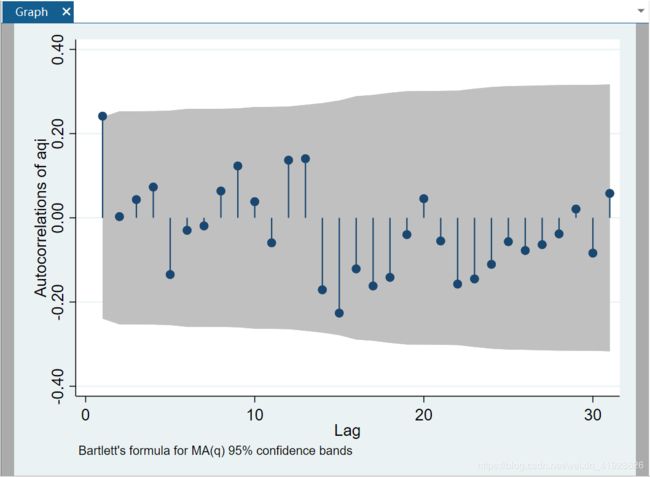
图4：偏自相关图

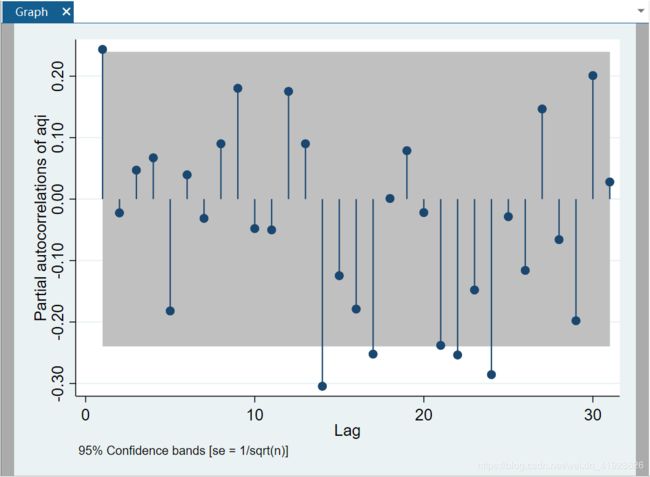
由时间序列的 ACF 与 PACF 图像均拖尾可知，该时间序列模型为 ARIMA 模型，根据时间序列的偏自相关图与自相关图，推测 p 值与 q 值均为 1。为了保证模型更加准确，尝试将多个 ARIMA 模型并分别计算其 AIC 和 BIC 值，判断准则： AIC 与 BIC 值相对越小，模型的拟合效果越优。发现却是 ARIMA(1， 0)模型最优。

模型比较

---------------------------------------------------------------------------
                 (1)          (2)          (3)          (4)          (5)   
              arma10       arma11       arma20       arma30       arma31   
---------------------------------------------------------------------------
aqi                                                                        
_cons          72.91***     72.86***     72.87***     72.91***     72.84***
             (31.23)      (31.97)      (31.63)      (29.42)      (32.63)   
---------------------------------------------------------------------------
ARMA                                                                       
L.ar           0.269**      0.127        0.272*       0.272*      -0.530   
              (2.63)       (0.27)       (2.16)       (2.05)      (-0.85)   
L2.ar                                  -0.0316      -0.0421        0.194   
                                       (-0.23)      (-0.28)       (1.00)   
L3.ar                                                0.0590      -0.0899   
                                                     (0.34)      (-0.66)   
L.ma                        0.145                                  0.808   
                           (0.29)                                 (1.30)   
---------------------------------------------------------------------------
sigma                                                                      
_cons          12.97***     12.96***     12.96***     12.94***     12.90***
             (11.95)      (11.84)      (11.78)      (11.84)      (11.35)   
---------------------------------------------------------------------------
N                 67           67           67           67           67   
ll            -266.8       -266.8       -266.8       -266.7       -266.5   
aic            539.6        541.5        541.5        543.4        544.9   
bic            546.2        550.3        550.3        554.4        558.2   
---------------------------------------------------------------------------
t statistics in parentheses
* p<0.05, ** p<0.01, *** p<0.001

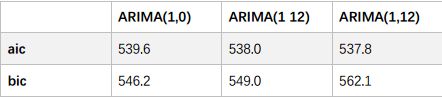
模型进一步比较

考虑到一年十二个月的气候相对一致，增加两个模型ARIMA（1 12）（只考虑第十二项滞后）与 **ARIMA（1，12）**进行对比，结果如下：

--------------------------------------------
                      (1)             (2)   
                  arma112        arma1_12   
--------------------------------------------
aqi                                         
_cons               73.25***        72.65***
                  (18.17)        (106.46)   
--------------------------------------------
ARMA                                        
L.ar                0.675***       -0.544   
                   (3.72)         (-1.89)   
L.ma               -0.454           0.882   
                  (-1.66)          (1.63)   
L12.ma              0.404*         -0.589** 
                   (2.09)         (-3.10)   
L2.ma                               0.303   
                                   (0.89)   
L3.ma                             -0.0304   
                                  (-0.08)   
L4.ma                              -0.116   
                                      (.)   
L5.ma                              -0.454*  
                                  (-2.32)   
L6.ma                              -0.347   
                                      (.)   
L7.ma                              -0.410   
                                  (-1.53)   
L8.ma                              -0.204   
                                  (-0.50)   
L9.ma                               0.167   
                                      (.)   
L10.ma                              0.214   
                                   (0.88)   
L11.ma                             -0.416   
                                  (-1.11)   
--------------------------------------------
sigma                                       
_cons               12.15***        10.17   
                   (9.53)             (.)   
--------------------------------------------
N                      67              67   
ll                 -264.0          -257.9   
aic                 538.0           537.8   
bic                 549.0           562.1   
--------------------------------------------
t statistics in parentheses
* p<0.05, ** p<0.01, *** p<0.001

模型选择

AIC 信息准则即 Akaike information criterion，是衡量统计模型拟合优良性的一种标准，它建立在熵的概念基础上，可以权衡所估计模型的复杂度和此模型拟合数据的优良性。

BIC 信息准则即 Bayesian Information Criterion， 是主观贝叶斯派归纳理论的重要组成部分。是在不完全情报下，对部分未知的状态用主观概率估计，然后用贝叶斯公式对发生概率进行修正，最后再利用期望值和修正概率做出最优决策。
表达式为：

AIC=2k - 2ln（L）
BIC = k*ln(n) - 2ln(L)
（公式中 k为模型参数个数， n 为样本个数， L 为模型极大似然函数值）

因为使用数据样本不大，文章偏重考虑 AIC 值最小的 ARIMA（1，12）模型，模拟效果更优。

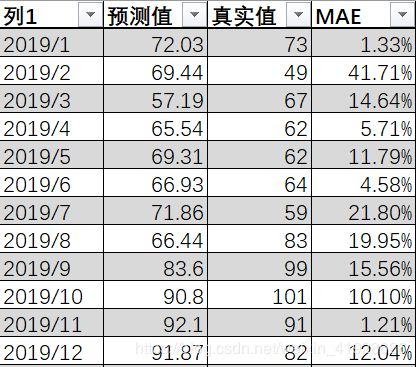
诊断与检验

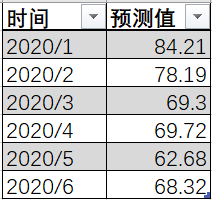
运行程序后将结果汇总在excel表，展示如下：

模拟预测2019年空气质量指数

平均绝对误差为13.36%

预测2020年1-6月空气质量指数

反思

1. 文章采用 ARIMA模型对广州空气质量指数进行时间序列分析预测，预测结果大体还算满意，个别值的误差较大，有非常大的改进空间，尤其是模型识别部分，如何构建拟合程度最优的模型是今后的研究方向。
2. 空气污染指数的取值范围定为 0～500，其中 0～50、51～100、 101～200、201～300 和大于 300，分别对应国家空气质量标准中日均值的 I 级、 II 级、 III 级、 IV级和 V 级标准的污染物浓度限定数值，根据预测数值可知广州未来半年将处于II 级的位置，空气质量评估为良，对人体健康无显著影响。广州空气质量持续保持高水平，让本地居民安心进行晨练夜跑等锻炼活动。
3. 文章在进行模型识别时考虑到月度影响，使得模型更加准确，可并未将政策影响纳入模型参数中，如广州市在 2017 年 10 月出台《广州市环境空气质量达标规划(征求意见稿)》的影响未在模型中体现出来，这时本文模型构建所忽略的部分，也是未来研究的方向之一。

参考文献

1. 空气质量多模式系统在广州应用及对 PM10 预报效果评估[J]. 陈焕盛,王自发,吴其重,吴剑斌,晏平仲,唐晓,王哲. 气候与环境研究. 2013(04)
2. 基于 ARIMA 时间序列的广州空气质量分析[J].林植林,莫斌.湖南工业职业技术学院学报,2014,14(04)
3. 珠三角区域空气质量预报方法及预报效果评估[J]. 叶斯琪,陈多宏,谢敏,谢智,汪宇,潘月云,沈劲,许凡. 环境监控与预警. 2016(03)
4. 天津市基于新标准的空气质量预报模型效果评估[J]. 高璟赟,杨宁,毕温凯,肖致美,陈魁,李源. 环境监控与预警. 2016(06)
5. 时间序列分析方法在上海地铁能耗预测中的应用[J].曹嘉晟,杨太华.能源与环境,2019(03)