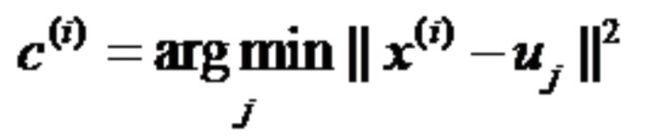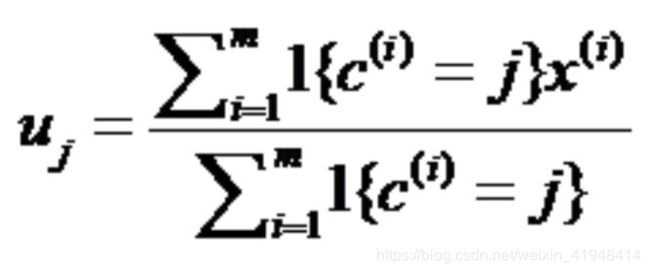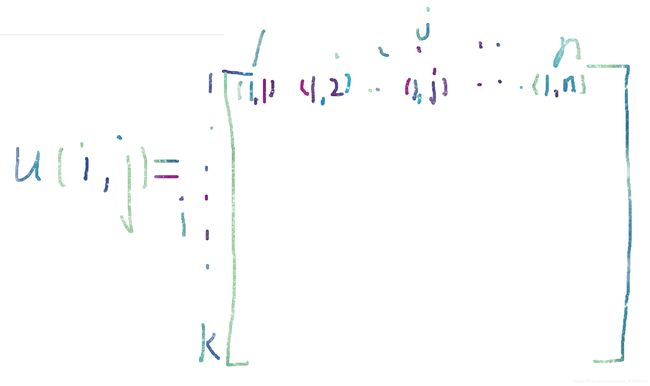k-means+matlab 之辣鸡学算法

首先，把 偷来 借鉴来的博文贴上，然后就开始漫漫求生路。
matlab练习程序（k-means聚类）
研究的过程中发现不少人引以为用，足以见其效用啦。

一、了解算法含义

1. 首先准备原始数据{x1，x2，…xn}，是不带标记的。
   在现实生活中可能是你待聚类的大数据。
2. 初始化k个随机数据{u1，u2，…uk}，即初始分配的聚类中心。

在1，2中 x ’ 空格 ’ 和 u ’ 空格 ’ 都是向量。其中，概念“向量”表示1×n 为行向量、n×1 为列向量。如果要表示一个人的身高体重，用向量（high，weight）。所以这里的向量相当于被描述对象的属性。

根据两公式求出最终所有的u，u是最终所有类的聚类中心。

公式一：

求出所有原始数据和初始聚类中心的距离，然后找出离每个初始聚类中心最近的原始数据。

变量：

1. arg j min 函数用法

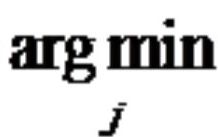
例如：arg x min f(x)
如果只有一个值使函数 f(x) 取最小值，则arg为该值，x。其中下标 x 的位置写后面函数的变量，如果有取值范围则写出，如：x属于[0，4Π]或x属于R。

如果有多个值使函数取最小值，则arg为集合。
如果无法取最小值，则无定义。
如果min换为max，同理。

在这里j是变量，代表先确定原始数据，之后不断地改变聚类中心。也就是拿聚类中心去试原始数据，看原始离哪个聚类中心最近。

2. || x(i) - uj ||下标2
   例如 ||x||下标2， 表示2-范数（欧式距离） = 各分量 x(i) 的平方和再开方。
   所以这里是x(i) - uj，原始数据的各个分量减去聚类中心的各个分量再开方。

感觉公式里c、x、|| ||外的上标该改成下标。

公式一总结：求出原始数据与聚类中心的距离，并把距离该原始数据最近的聚类中心的值赋给 c(i) 。

问题：如果算出距离相等怎么办？
答：随机划分。反正要是下次换聚类中心了距离可能就不一样了。

公式二：

恕我直言，这个公式没看懂。

解释长这样：

求出所有和这个初始聚类中心最近的原始数据的距离的均值，做聚类中心

然后不断迭代这两个公式，直到所有的 u 都不怎么变就完成了。

二、引用例子理解

1. 大哥法（原始数据一维，也就是大家都只是一个数）
   K-means算法之门派风云
2. 大哥法（原始数据二维，也就是个坐标）
   K-Means算法之经典大哥法
   害怕链接丢了，我还是偷一部分贴上吧。

炒鸡有助于理解，一定要结合前面的公式弄懂了。

---

K-Means 聚类算法的大致意思就是“物以类聚，人以群分”：

1、首先输入 k 的值，即我们指定希望通过聚类得到 k 个分组；
2、从数据集中随机选取 k 个数据点作为初始大佬（质心）；
3、对集合中每一个小弟，计算与每一个大佬的距离，离哪个大佬距离近，就跟定哪个大佬。
4、这时每一个大佬手下都聚集了一票小弟，这时候召开选举大会，每一群选出新的大佬（即通过算法选出新的质心）。
5、如果新大佬和老大佬之间的距离小于某一个设置的阈值（表示重新计算的质心的位置变化不大，趋于稳定，或者说收敛），可以认为我们进行的聚类已经达到期望的结果，算法终止。
6、如果新大佬和老大佬距离变化很大，需要迭代3~5步骤。

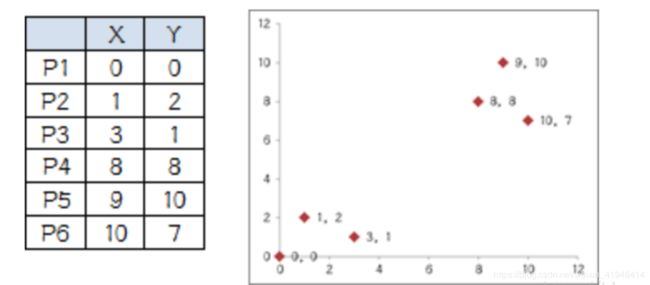
说了这么多，估计还是有点糊涂，下面举个非常形象简单的例子：

有6个点，从图上看应该可以分成两堆，前三个点一堆，后三个点另一堆。现在我手工地把 k-means 计算过程演示一下，同时检验是不是和预期一致：

1.设定 k 值为2
2.选择初始大佬（就选 P1 和 P2）
3.计算小弟与大佬的距离：

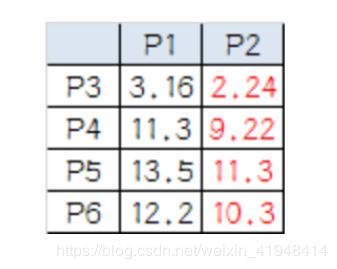
从上图可以看出，所有的小弟都离 P2 更近，所以次站队的结果是：
A 组：P1
B 组：P2、P3、P4、P5、P6
4.召开选举大会：
A 组没什么可选的，大佬就是自己

B 组有5个人，需要重新选大佬，这里要注意选大佬的方法是每个人 X 坐标的平均值和 Y 坐标的平均值组成的新的点，为新大佬，也就是说这个大佬是“虚拟的”。因此，B 组选出新大哥的坐标为：P 哥（（1+3+8+9+10）/5，（2+1+8+10+7）/5）=（6.2，5.6）。

综合两组，新大哥为 P1（0，0），P哥（6.2，5.6），而P2-P6重新成为小弟。
5.再次计算小弟到大佬的距离：

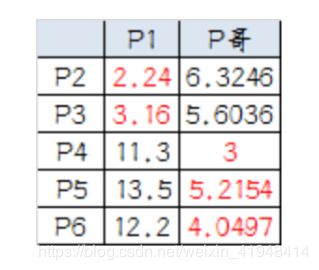
这时可以看到P2、P3离P1更近，P4、P5、P6离P哥更近，所以第二次站队的结果是：
A 组：P1、P2、P3
B 组：P4、P5、P6（虚拟大哥这时候消失）
6.第二届选举大会：
同样的方法选出新的虚拟大佬：P哥1（1.33，1），P哥2（9，8.33），P1-P6都成为小弟。
7.第三次计算小弟到大佬的距离：

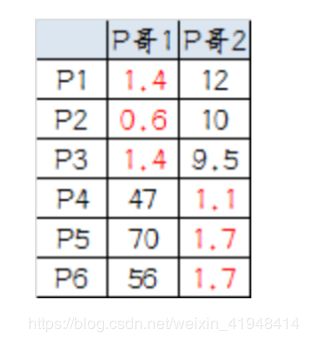
这时可以看到 P1、P2、P3 离 P哥1 更近，P4、P5、P6离 P哥2 更近，所以第二次站队的结果是：
A 组：P1、P2、P3
B 组：P4、P5、P6
我们可以发现，这次站队的结果和上次没有任何变化了，说明已经收敛，聚类结束，聚类结果和我们最开始设想的结果完全一致。

三、算法代码“超”详解

main.m

clear all;%清除工作空间的所有变量，函数，和MEX文件
close all;%关闭所有的Figure窗口 
clc;%清除命令窗口的内容，对工作环境中的全部变量无任何影响 

%第一类数据
mu1=[0 0 0];  %均值，见详解
S1=[0.3 0 0;0 0.35 0;0 0 0.3];  %协方差，见详解
data1=mvnrnd(mu1,S1,100);   %产生高斯分布数据，见详解

%%第二类数据
mu2=[1.25 1.25 1.25];
S2=[0.3 0 0;0 0.35 0;0 0 0.3];
data2=mvnrnd(mu2,S2,100);

%第三类数据
mu3=[-1.25 1.25 -1.25];
S3=[0.3 0 0;0 0.35 0;0 0 0.3];
data3=mvnrnd(mu3,S3,100);


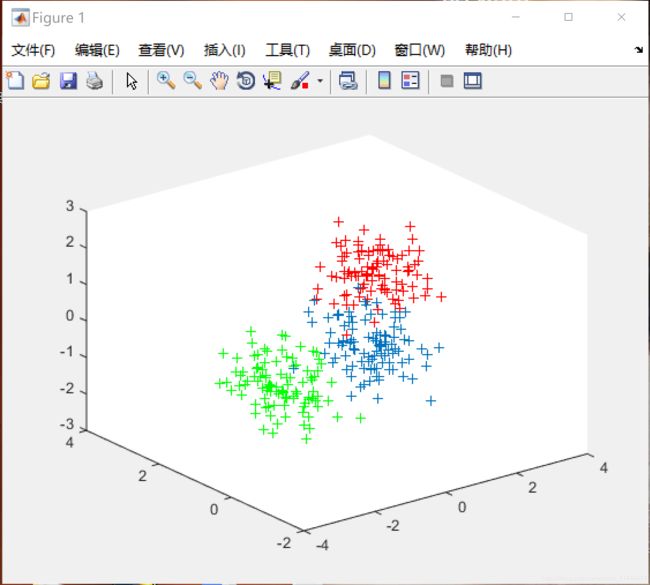
%显示数据
plot3(data1(:,1),data1(:,2),data1(:,3),'+');
hold on;
plot3(data2(:,1),data2(:,2),data2(:,3),'r+');
plot3(data3(:,1),data3(:,2),data3(:,3),'g+');
grid on;//显示坐标轴网格线


%三类数据合成一个不带标号的数据类
data=[data1;data2;data3];   %把三组数据看成整体再划分

%k-means聚类
[re u]=KMeans(data,3);  %最后产生带标号的数据，标号在所有数据的最后，数据再加一维度
[m n]=size(re);%表示re矩阵的大小m行n列

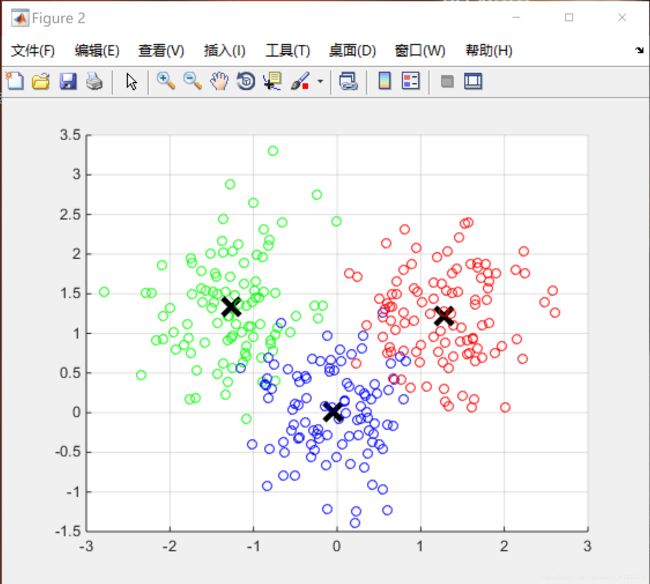
%最后显示聚类后的数据
figure;%打开一个窗口，浮于当前界面之上，直到新的窗口被唤醒
hold on;
for i=1:m 
    if re(i,4)==1   
         plot3(re(i,1),re(i,2),re(i,3),'ro'); 
    elseif re(i,4)==2
         plot3(re(i,1),re(i,2),re(i,3),'go'); 
    else 
         plot3(re(i,1),re(i,2),re(i,3),'bo'); 
    end
end
plot3(u(:,1),u(:,2),u(:,3),'kx','MarkerSize',14,'LineWidth',4);
grid on;

第一类数据

mu1=[0 0 0]; %均值
如果内部3（2）个数，生成三个（两个）数组成的行向量

S1=[0.3 0 0;0 0.35 0;0 0 0.3]; %协方差
生成一个3×3（2×2）的矩阵

data1=mvnrnd(mu1,S1,100); %产生高斯分布数据
生成100行，3（2）列的数据矩阵，其中三列（两列）分别为100个值的100个坐标（x，y，z）在三维空间（（x，y）在二维空间）

mvnrnd()：生成多维（正态分布 = 高斯分布）数据，n维d列的均值为mu，协方差为SIGMA（S1）的矩阵。

mu1：表示需要生成数据的均值。

S1：需要生成的数据的自相关矩阵（相关系数矩阵）

产生高斯分布数据，需要均值为0，即mu1=0，标准差S1可取任意正数。S1越小，随机变量数值越集中在mu1附近，平均值越接近0。

想产生几类数据就设几遍 mu S data，最后显示数值时若两类则有两组，三类则三组数据。

---

显示数据

plot3(data1(:,1),data1(:,2),data1(:,3),’+’);

表示取data1的第一列，第二列，第三列，以加号表示画图。

plot3（）函数可绘制3D图形

plot函数用法：plot(X，Y，LineSpec)
X由所有输入点坐标的x组成
Y由X中包含的x对应的y所组成
LineSpec是用户指定的绘图样式

• +…加号
• o…圆
• *…星号
• ·…点
• g…绿色
• r…红色
• r+…红色加号
• g+…绿色加号

---

grid on：显示坐标轴网格线
grid off：隐藏坐标轴网格线
hold on：在当前坐标系中画了一幅图后再画一副，原来的与新图共存。
hold off：在当前坐标系中画了一幅图后再画一副时之前的图被替代。

---

k-means聚类

[re u]=KMeans(data,3);

data：MN的矩阵，待聚类的原始数据
3 = K：是data的聚类个数，与u相关
re：N1的向量，存储的是每组原始数据的聚类标号，类似于label
u：K*N的矩阵，存储的是K个聚类中心的位置

Kmeans（）函数表示把data矩阵分3类，之后返回每个点的聚类标号给u，最终聚类中心的位置给re

还有其他形式的Kmeans（）函数

• Index = Kmeans（A，K）
• [Index，C，sumD] = Kmeans（A，K）
• […] = Kmeans（…，‘Param1’，‘Val1’，‘Param2’，‘Val2’，…）

有兴趣可自行查阅

---

显示聚类后的数据

for i=1:m 
if re(i,4)==1   
%表示矩阵re中的第i行（从第一组数据到最后一组）第4个数据，也就是聚类后新加的一维标签列，判断是否为1，也就是是否属于第一组聚类？
     plot3(re(i,1),re(i,2),re(i,3),'ro'); 
     %  如果是，则根据该组数据的坐标画出聚类后的图。
elseif re(i,4)==2
     plot3(re(i,1),re(i,2),re(i,3),'go'); 
else 
     plot3(re(i,1),re(i,2),re(i,3),'bo'); 
end
end

---

从main函数调用kmeans函数开始就涉及到kmeans函数的内容了，所以分析所调用的kmeans函数会有助于理解。

首先说明：
由代码里的function文字识别出，Kmeans函数是一个function函数文件，不是脚本文件。
把main函数和kmeans函数单独写也是为了方便函数之间相互调用。

KMeans.m

%N是数据一共分多少类
%data是输入的不带分类标号的数据
%u是每一类的中心
%re是返回的带分类标号的数据
%部分一：这一部分属于以设零矩阵的方式提前限定聚类中心的取值范围
function [re u]=KMeans(data,N)   
    [m n]=size(data);   %m是数据个数，n是数据维数
    ma=zeros(n);        %每一维最大的数
    mi=zeros(n);        %每一维最小的数
    u=zeros(N,n);       %随机初始化，在用u(i,j)之前都要这么做。最终迭代到每一类的中心位置
    for i=1:n          
       ma(i)=max(data(:,i));    %每一维最大的数
       mi(i)=min(data(:,i));    %每一维最小的数
       for j=1:N
            u(j,i)=ma(i)+(mi(i)-ma(i))*rand();  %随机初始化，不过最好在每一维[min max]中初始化
       end      
    end
%部分二：求出中心与原始数据的距离   
    while 1
        pre_u=u;            %首先把上一次求得的中心位置放到pre_u中，为到末尾进行pre_u与u的比较做准备
        for i=1:N           %固定聚类中心个数
            tmp{i}=[];      % 公式一中的x(i)-uj,为公式一实现做准备
            for j=1:m       %遍历原始数据行数
                tmp{i}=[tmp{i};data(j,:)-u(i,:)];
            end
        end
%部分三：实现公式一        
        quan=zeros(m,N);
        for i=1:m        %公式一的实现
            c=[];
            for j=1:N
                c=[c norm(tmp{j}(i,:))];
            end
            [junk index]=min(c);
            quan(i,index)=1;              
        end
        
%部分四：实现公式二，设定打破循环条件
        for i=1:N            %公式二的实现
           for j=1:n
                u(i,j)=sum(quan(:,i).*data(:,j))/sum(quan(:,i));
           end           
        end
        
        if norm(pre_u-u)<0.1  %不断迭代直到位置不再变化
            break;
        end
    end
%部分五：    定义要返回的re值
    re=[];
    for i=1:m
        tmp=[];
        for j=1:N
            tmp=[tmp norm(data(i,:)-u(j,:))];
        end
        [junk index]=min(tmp);
        re=[re;data(i,:) index];
    end
    
end

部分一：

zeros（）函数

ma=zeros(n); %每一维最大的数
其中zeros()函数表示生成一个n×n的零矩阵
同理
u=zeros(N,n);
表示生成N×n的零矩阵

rand（）函数

rand () 函数产生在（0，1）之间均匀分布的随机数组成的数组。
不带参数的情况rand () 表示产生均值为0，方差为1的随机矩阵，也是标准正态分布的随机矩阵。

为什么要生成随机矩阵？

• 初始化时如果b = np.zeros((2,1))，b全赋0值，会产生对称性。为避免该现象，随机生成一些数据赋值则不用担心对称性。

为什么用ma(i)+(mi(i)-ma(i))*rand();？

• 是为了保证初始化的中心值在最大值和最小值之间。

为什么出现u(j,i)这么别扭的数？

• 因为想先以i循环，后以j循环。同时又必须先以维数为准固定住，再遍历聚类中心行数。所以令i = n，j = N。随之出现先固定维数，行数改变的u（j，i）

部分二：

从 while 1开始进入大循环。由于1永远为真，所以while永远循环，直到找到break打破循环

关于花括号{}

        tmp{i}=[];       

%赋空矩阵给名为tmp的元胞数组。

花括号 {} 表示一个元胞数组，用于元胞型的数组的分配或引用。元胞数组的每个单元中可存放不同的数据类型，如数值、字符、矩阵、数组。
小括号（）引用数组的元素
X（3）代表X的第三个元素。
中括号 [] 构建向量或矩阵
X（[1 2 3]）代表X的头三个元素。

            tmp{i}=[tmp{i};data(j,:)-u(i,:)];   % 计算x(i)-uj,为公式一实现做准备

关于 tmp{i}=[tmp{i};…];且tmp{i}=[];
解释为先弄一个空矩阵，之后把后面（…）输出的数据放到空矩阵中。
如：
Data = [];
Data = [Data;a];
表示把a作为一列加入到Data中，a是列向量就竖着一列一列加，a是行向量就一行一行加。

由此可知，tmp{i}中放的是先固定聚类中心，得到每一行原始数据与所有聚类中心的距离。

部分三：

quan=zeros(m,N);
把m行N列零矩阵赋给quan，初始化。

c=[c norm(tmp{j}(i,:))];
就是公式一，还是往空矩阵中加数据
[]中的空格表示一行一行加数据，
如果是；则是一列一列加数据
如下图：
i——[1…m];外循环遍历
j——[1…N];内循环遍历

norm()函数

其中norm（）函数表示求范数。
如果norm（A）中的A是矩阵，则求矩阵的最大奇异值。
如果norm（A）中的A是向量，则求向量二范数。
如果norm(A,p)，则求向量A的p范数。

lp范数（p范数）：

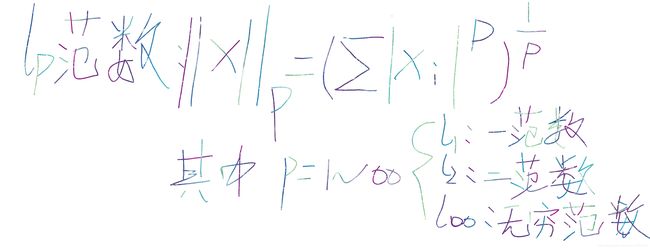
二范数（p=2)也叫欧几里得范数，也是k-means算法所用的计算距离公式。

norm()函数内部的变量：

tmp{j}(i,:)
如a{i}(j)中i表示访问第i个元胞，j表示访问第i个元胞中的第j个数。

由此可知，要找tmp 第j个元胞的第i个数。由取值范围可知，j取值1-N，与部分二中的i取值相同，所以部分三中的tmp{j}=部分二中的tmp{i}，而tmp{i}中装着原始数据与中心的距离。求第二部分tmp第i个元胞的第j个数，表示先拿第一个原始数据和第一个中心的距离（坐标），用欧几里得距离（norm()函数）计算成好比较的数，并不断赋值到名为c的空矩阵中。之后遍历聚类中心，表示保持第一个原始数据不动拿出距所有聚类中心的距离。之后依次换原始数据。

min()函数

[junk index]=min（c);

如[m,j] = min(e)表示返回矩阵e中最小值的位置
m记录e的每列最小值，j记录每列最小值行号。

运行时提示junk改为~，因为在matlab运行之前由于没有使用，所以替换
~：
①表示“与”或“非”中的“非”；
②表示参数缺省（比如size()函数会返回[row,col]，如果我们只要row，可以写成[row,~]）

c矩阵如下图所示，所以找到的每列最小值就是离每个原始数据最近的聚类中心的距离，并得到聚类中心的序号，也就聚类出所有数据属于哪些聚类中心。

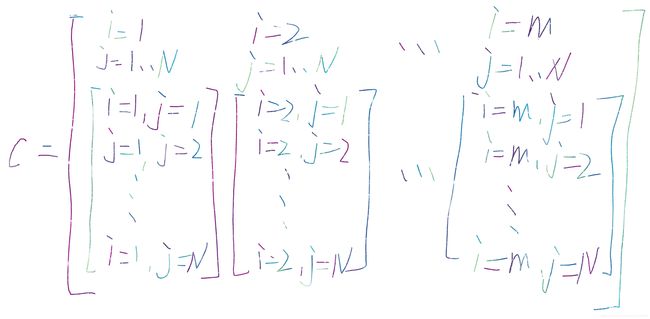
quan(i,index)=1;
表示把quan零矩阵中i行（原始数据）对应的自身聚类中心序号的位置赋值为1，这样选中为1，未选中为0，聚类中心显而易见。
如图，假如所有原始数据属于的聚类中心长这样

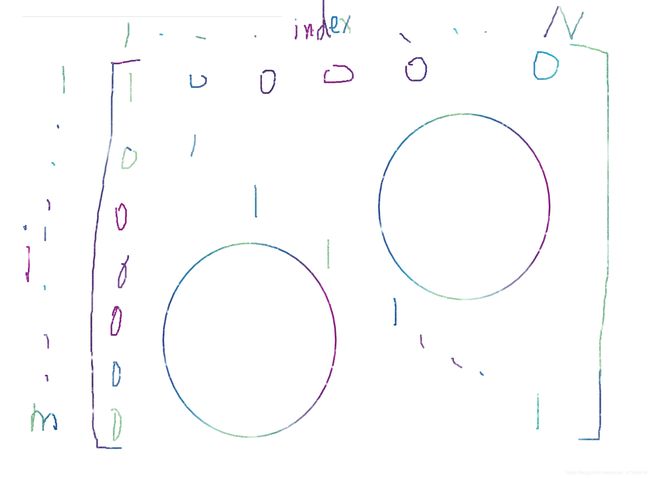
部分四：

u(i,j)=sum(quan(:,i).*data(:,j))/sum(quan(:,i));

公式二是以每个类为单位，自己算自己的新的聚类中心。
方法为：求每个类中所有原始数据与中心的距离的均值。

quan(:,i)中的i范围为1:N，是部分三中的quan(:,index)，所以要从quan(:,i)开始，在quan的第一列找为1的位置，也就是通过相乘的方式找序号为1的聚类中心包括哪些原始数据。有1可以计算，剩余位置为0。

点乘和叉乘

点乘：对应位置的数相乘
叉乘：矩阵相乘

如：
a = [1 2 3]
b = [4;5;6]
c = a*b

输出：c = [1 2 3]·[4;5;6] = 32

d = a.*b

输出：d =[1 2 3][4;5;6]
输出错误

e = [7 8 9]
d = a.*e
输出：d = [1 2 3][7 8 9] = [7 16 27]

sum()函数

若X为向量，sum(X)为向量元素之和
若X为矩阵，sum(X)为一个行向量（由每一列元素之和组成）

data(:,j)表示原始数据的第1-n列
由此可知：
sum(quan(:,i).*data(:,j))如图

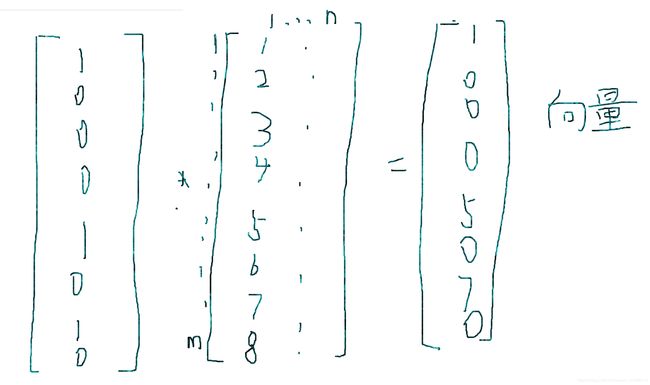
所以sum中的值为向量，需要把向量的值相加，就是把所有属于第一个聚类中心的原始数据都相加。再除以属于第一个聚类中心的原始数据的个数，平均后的值放入u(1,1)，就完成了公式二

当data(:,j)中j从1-n遍历时表示抽取构成原始数据的所有坐标，依次去乘判断是否属于聚类中心的[0-1]矩阵，平均后再赋值给u(i,j)

if norm(pre_u-u)<0.1
表示如果前一个保存好的聚类中心与新产生的聚类中心之间的欧几里得距离小于0.1，应该就是聚类中心不变了，所以打破while循环

部分五：

tmp=[tmp norm(data(i,:)-u(j,:))];
把所有原始数据与最终确定的中心的距离算出，并放入tmp中

[junk index]=min(tmp);
把tmp矩阵中每列最小值输出为junk，每列最小值行号输出为index

re=[re;data(i,:) index];
index表示加一列，记录行号
把矩阵data(i,:)和index纵向拼接

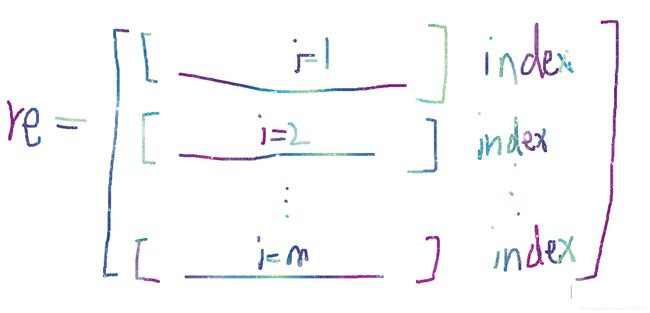
至此，kmeans彻底结束。

回头看看main函数的最后一部分

打开窗口，遍历原始数据从1-m

if re(i,4)==1
plot3(re(i,1),re(i,2),re(i,3),‘ro’);
表示如果re矩阵遍历到的某个原始数据的最后一列，聚类中心标号列为1，则，根据该数据的（x,y,z）输出该值的位置，并以不同的颜色区分聚类中心。

同理，输出中心标号为2，3的值。

plot3（）函数

plot3(u(:,1),u(:,2),u(:,3),‘kx’,‘MarkerSize’,14,‘LineWidth’,4);

取出聚类中心矩阵u的第一列（y1,y2,y3)、第二列(k1,k2,k3)、第三列(r1,r2,r3)数据，整理出给了三个点的坐标，（y1,k1,r1),(y2,k2,r2), (y3,k3,r3)。kx中k是黑色，x是x线。‘Markersize’表示标记尺寸为14，也就是黑色x线的大小为14，'LineWidth’表示线宽4号。

如plot3([x,x,x+1000,x+1000,x],[y,y-1000,y-1000,y,y],[z,z,z,z,z]);
给了5个点的坐标，第一个点是（x，y，z），第三个点是（x+1000，y-1000，z）；默认情况下是把点连成线，可以更改参数，如画点而不连线。

==当遇到不理解的指令时，在命令行输入 'doc+你不理解的指令’即可 ==

四、显示结果

东抄抄西学学，希望接下来的研究顺顺利利。

下一个不出意外的话是DTW算法代码研究。
然后看能不能铜鼓到一块去再改进。