数据研发学习笔记08:数据预处理
文章目录
- 1 数据预处理基本思想
- 2 数据规范化
- 2.1 最小-最大法(min-max normalization)
- 2.2 零均值规范化(z-score)
- 3 数据离散化
- 3.1 等距离(equal- distance)分箱
- 3.2 等频率(equal-frequency)分箱
- 3.3 基于熵的离散化方法
- 3.4 ChiMerge方法
- 4 数据清洗
- 4.1 处理缺失数据
- 4.2 处理噪音数据
- 5 特征提取与特征选择
- 5.1 特征提取
- 5.2 特征选择
1 数据预处理基本思想
- 数据在搜集时由于各种原因可能存在缺失、错误、不一致等问题
- 用于描述对象的数据有可能不能很好地反映潜在的模式
- 描述对象的属性的数量可能有很多,有些属性是无用的或者冗余的
数据预处理的任务:
(1)数据规范化(normalization)
(2)数据离散化(discretization)
(3)数据清洗(data cleaning)
(4)特征提取与特征选择
2 数据规范化
数据规范化又称标准化(standardization),通过将属性的取值范围进行统一,避免不同的属性在数据分析的过程中具有不平等的地位。
常用方法如下:
2.1 最小-最大法(min-max normalization)
假设需要映射到目标区间为[L,R ]。原来的取值范围为[l, r ],则根据等比例映射的原理,一个值x映射到新区间后的值v的计算方法如下:
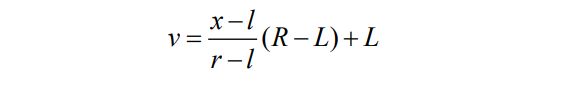
例如,对于描述客户的属性“年收入(万元)”,如果原来的取值范围为[3,200],新的取值范围为[0,1],则若某客户的年收入为60万元,规范化后为(60-3)/(200-3)=0.29
2.2 零均值规范化(z-score)
z-score,又称零均值规范化(zero-mean normalization)。给定一个属性 A,设其取值的均值为µA,标准差为ρA,A的某个取值x 规范化后的值v 计算如下:
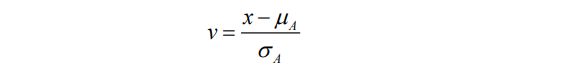
均值为µA 和标准差为ρA 通过已有样本的属性值进行计算。规范化后的属性A取值的均值为零。
例如,年收入属性的均值为82,标准差为39,则年收入60万规范化后为-0.56
3 数据离散化
3.1 等距离(equal- distance)分箱
又称为等宽度分箱(equal-width binning),是将每个取值映射到
等大小的区间的方法。
给定属性A的最小和最大取值分别为min和max,若区间个数为k,则每个区间的间距为I=(max-min)/k,区间分别为[min,min+I)、[min+I, min+2I)、…、[min+(k-1)I, min+kI]。
等距离分箱可能导致属于某些的取值非常多,而某些又非常少。
3.2 等频率(equal-frequency)分箱
又称等深度分箱(equal-depth binning)。它将每个取值映射到一个区间,每个区间内包含的取值个数大致相同。
例如:
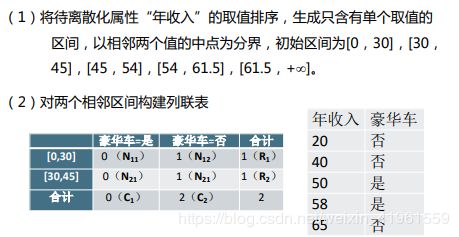
假设14个客户的属性“年收入”的取值按顺序为:
20,40,50,58,65,80,80,82,86,90,96,105,120,200
- 利用等距离分箱,区间的个数为4,则区间间距为(200-20)/4=45,则4
个箱的区间分别为[20,65),[65,110),[110,155),[155,200] - 利用等频率分箱,每箱3个值,则4个箱分别为[20,40,50],[58,65,80,80],[82,86,90],[96,105,120,200]
3.3 基于熵的离散化方法
分箱离散化是一种无监督离散化方法。基于熵的离散化方法是常用的有监督的离散化方法:给定一个数据集D及分类属性的取值,即类别集合C={c1, c2, …, ck},数据集D的信息熵entropy(D)的计算公式:
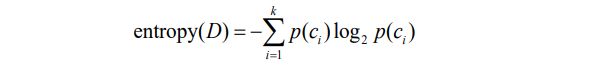
其中p(ci)=count(ci)/|D|,count(ci)表示类别ci在D中出现的次数,|D|代表D中的数据行数,即对象个数。信息熵的取值越小,类别分布越纯,反之越不纯。
首先将D中的行按照属性A的取值进行排序。
分割的方法是利用条件A£v,v 是A的一个取值。相应地,数据集D按照此条件分裂为两个子数据集:D1, D2,综合这2个子数据集的信息熵作为衡量这种分割优劣的度量,entropy(D, v):
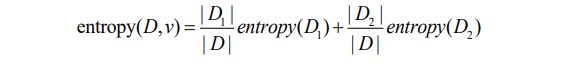
一个数据集D按A≤v分裂前后信息熵的差值称为信息增益,记为gain(D,v):
![]()

3.4 ChiMerge方法
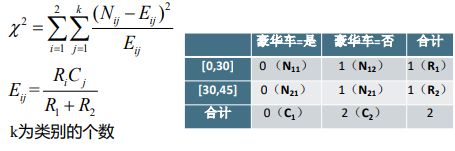
如果基于熵的方法可以看作是自顶向下的分裂方法,则ChiMerge则属于自底向上的合并方法。
ChiMerge则是从每个值都是一个小区间开始,不断合并相邻区间成为大的区间,它是基于统计量卡方检验实现的。

4 数据清洗
数据清洗主要包括:处理数据的缺失、噪音数据的处理以及数据不一致的识别和处理。
该部分可参考笔记:
- 数据分析学习总结笔记05:缺失值分析及处理
- 数据分析学习总结笔记04:异常值处理
4.1 处理缺失数据
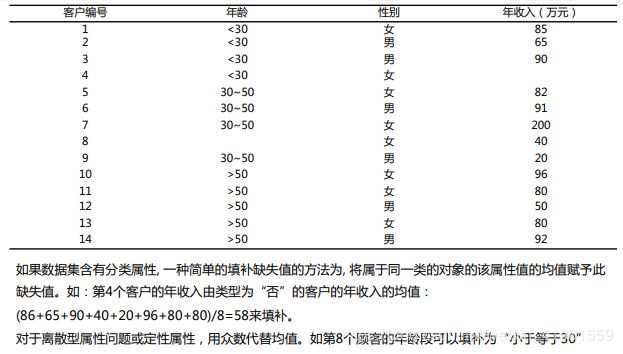
如果数据集含有分类属性,一种简单的填补缺失值的方法为,将属于同一类的对象的该属性值的均值赋予此缺失值;对于离散属性或定性属性,用众数代替均值。
4.2 处理噪音数据
一类是识别出噪音,将其去除;另一类是利用其它非噪音数据降低噪音的影响,起到平滑(smoothing)的作用。
- 孤立点的识别属于第一类方法,之前介绍聚类算法DBSCAN时提到过,最终不属于任一个簇的点可以看作噪音。
- 分箱(binning)方法可以用于平滑噪音。例如,将年收入的缺失值填补之后,将其取值利用分箱法平滑噪音。
5 特征提取与特征选择
5.1 特征提取
特征提取是指描述对象的属性不一定反映潜在的规律或模式,对属性进行重新组合,获得一组反映事物本质的少量的新的属性的过程。
主成分分析,PCA(principle component analysis) 最早由Karl Pearson于1901年提出,后经Harold Hotelling发展,是一种经典的统计方法。它通过对原有变量(属性、特征)进行线性变换,提取反映事物本质的新变量,同时去除冗余、降低噪音,达到降维的目的。


5.2 特征选择
特征选择是指从属性集合中选择那些重要的、与分析任务相关的子集的过程。
有效的特征选择不仅降低数据量,提高分类模型的构建效率,有时还可以提高分类准确率。
特征选择方法有很多,共同特点过程可以分为以下几步:
① 根据一定的方法选择一个属性子集
- 选择属性子集的方法一般采用启发式方法,只检验部分可能性比较大的子集,这样可以快速完成属性的选择。
- 常用的方法包括:逐步增加法(stepwise forward selection)、逐步递减法(stepwise backward elimination)、随机选取。
② 衡量子集的相关性
通常采用两类不同的方法:
- 一类称为filter方法,利用距离、信息熵以及相关度检验等方法直接衡量属性子集与类别的关联;
- 另一类称为wrapper方法,利用分类模型来衡量属性子集的效果,通常效率很低。
③ 判断是否需要更新属性子集,若是,转第1步继续;若否,进入下一步。
④ 输出最终选取的属性子集。