直观理解 梯度（gradient）

梯度

在机器学习中，我们通常需要对问题进行建模，然后可以得到一个成本函数(cost function)，通过对这个成本函数进行最小化，我们可以得到我们所需要的参数，从而得到具体的模型。这些优化问题中，只有少部分可以得到解析解(如最小二乘法)，而大部分这类优化问题只能迭代求解，而迭代求解中两种最常用的方法即梯度下降法与牛顿法。

梯度概念是建立在偏导数与方向导数概念基础上的。所谓偏导数，简单来说是对于一个多元函数，选定一个自变量并让其他自变量保持不变，只考察因变量与选定自变量的变化关系。数学上说，是指对于多元函数$y=f(x_1,x_2,...x_n)$，假设其偏导数都存在，则该函数共有$n$个偏导数，可以表示为：
$$f_{x_1}=\frac{\partial y}{\partial x_1},f_{x_2}=\frac{\partial y}{\partial x_2}...f_{x_n}=\frac{\partial y}{\partial x_n}$$

偏导数只能表示多元函数沿某个坐标轴方向的导数，如对于二元函数$z=x^2+y^2$ ，$\frac{\partial z}{\partial x}=2x$表示函数沿$X$轴方向的导数，而$\frac{\partial z}{\partial y}=2y$表示函数沿$Y$轴方向的导数。

除开沿坐标轴方向上的导数，多元函数在非坐标轴方向上也可以求导数，这种导数称为方向导数。很容易发现，多元函数在特定点的方向导数有无穷多个，表示函数值在各个方向上的增长速度。一个很自然的问题是：在这些方向导数中，是否存在一个最大的方向导数，如果有，其值是否唯一？为了回答这个问题，便需要引入梯度的概念。

一般来说，梯度可以定义为一个函数的全部偏导数构成的向量(这一点与偏导数与方向导数不同，两者都为标量)。一般将函数$f$的梯度记为$\nabla f$，即：

事实上，梯度向量的方向即为函数值增长最快的方向，为什么会如此，可以从几个角度去理解。

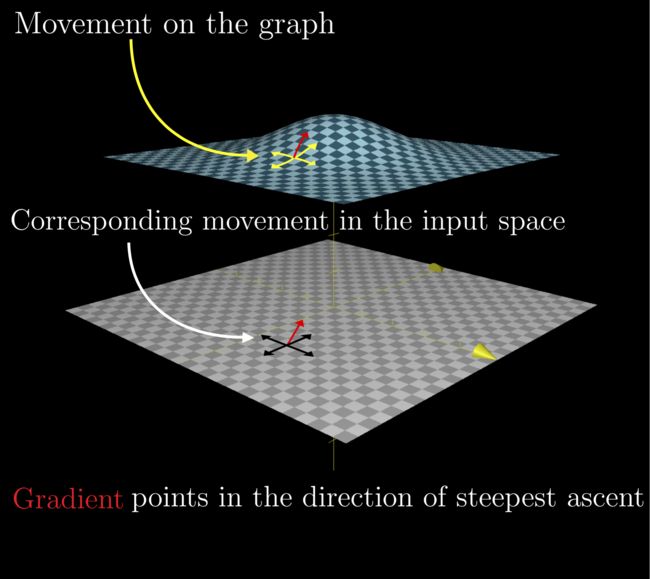
事实上，梯度向量的方向即为函数值增长最快的方向，为什么会如此，可以从几个角度去理解。
在上图中，我们可以看到，为了找到方向导数中的最大值，我们可以将其投影到$xy$平面来理解，这种投影方式对应的便是等高线图。如对于一个二元函数$z=f(x,y)$，我们可以画出它的等高线图如下：

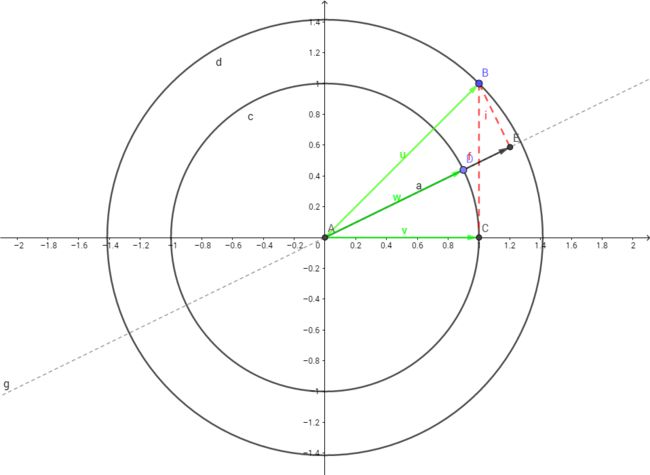
该函数的等高线图为圆心在原点的一系列圆，等高线的值由里向外逐渐增加。点$B(x,y)$为点$(x,y,z)$在$xy$平面上的投影，可以看到向量$AB$即为函数在点$(x,y,z)$处的梯度向量。根据方向导数的定义，方向导数$D_{u}f=f_x\cos \theta +f_y\sin \theta$,其中$\theta$为此向量与$X$正方向的夹角。由于梯度向量为$u=(f_x,f_y)$，单位向量$w=(cos\theta ,\sin \theta )$，则方向导数的大小可以表述为梯度向量与此单位向量的数量积，即：
$$D_{u}f=f_x\cos \theta +f_y\sin \theta =u\cdot w=|u|\cdot |w|\cdot \cos \alpha =|u|\cdot \cos \alpha$$

其中$\alpha$为梯度向量与单位向量之间的夹角，即$\angle BAD$。可以看出，方向导数的大小可以看作梯度向量在指示方向导数方向的单位向量上的投影，即线段$AE$的长度。显而易见，线段$AE$的长度小于线段$AB$的长度，也即梯度向量的模总是大于等于方向导数向量的模。这就解释了为什么沿着梯度向量方向是函数值增长最快的方向，而它正是函数所有偏导数构成的向量。

在上图中也可以看出，梯度向量垂直于等高线，这为我们提供了另一个观察梯度向量的角度。如对于函数$$f(x,y)=xy$$，其等高线图与梯度向量如下：

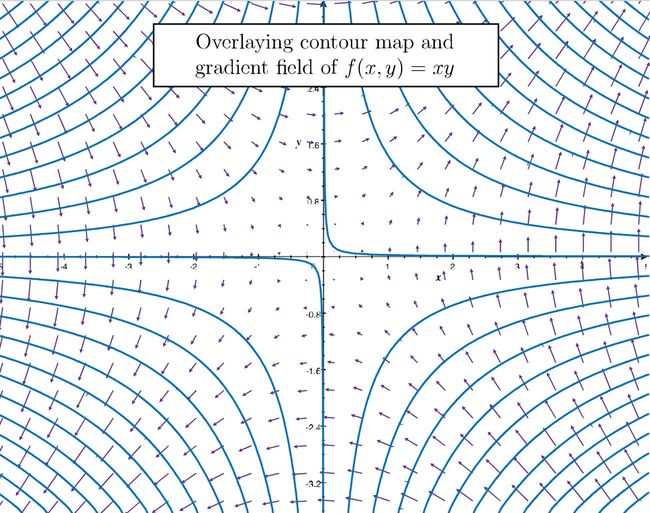
我们可以两个角度考虑：第一，在特定函数点，固定每次移动的步长，向那个方向移动函数值增长最快？第二，固定需要增加的函数值，向哪个方向需要移动的步长最短？

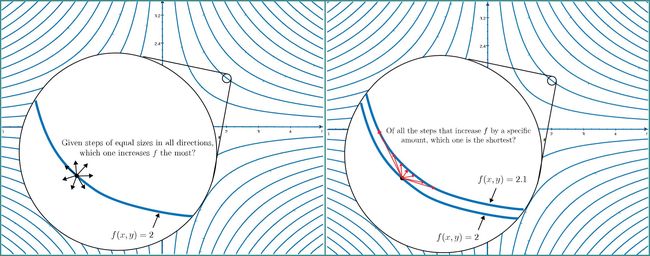
在左图中，固定移动的步长，我们可以看到垂直于等高线图的方向即为函数值增长最快的方向，也就是梯度向量指示的方向。在右图中，假设函数值有一个固定的微小的增长，则明显梯度向量指示的方向所需要的步长最短，而这个向量也是垂直于等高线的。

梯度下降或上升法正是基于梯度指示函数值增长最快的方向而产生的，利用这个方法，我们可以使用迭代的方法计算函数的最大或最小值，从而解决机器学习中遇到的最优化问题。

梯度和方向导数的关系

https://www.zhihu.com/question/36301367

Reference:
https://www.v2ex.com/t/397822