Python金融大数据分析——第10章 推断统计学 笔记2

第10章 推断统计学

Python金融大数据分析——第10章 推断统计学 笔记1
Python金融大数据分析——第10章 推断统计学 笔记2
Python金融大数据分析——第10章 推断统计学 笔记3

10.3 估值

蒙特卡洛模拟的最重要应用之一是未定权益（期权，衍生品，混合型工具等）的估值。简单地说，在风险中立的世界中，未定权益的价值是风险中立（鞅）测度下的折现后预期收益。这是所有风险因素（股票、指数等）偏离无风险短期利率的概率测度。根据资产定价基本定理，这种概率测度的存在等价于套利机会的缺失。

金融期权表示在规定（行权期）日期（欧式期权）或者规定时期（美式期权）内，以规定价格（所谓行权价 ） 购买（看涨期权 ） 或者出售（看跌期权）指定金融工具。我们首先考虑估值较为简单的情况一欧式期权。

10.3.1 欧式期权

基于某种指数的欧式看涨期权到期日收益通过公式 h(ST)≡max(ST−K,0) h ( S T ) ≡ m a x ( S T − K , 0 ) 得出，其中 ST S T 是到期日 T 的指数水平，K 是行权价格。给定相关随机过程（例如 几何布朗运动）的风险中立测度，或者在一个完备市场中，这种权证的价格由下面公式表示。

公式 风险中立预期定价

C0=e−rT∫∞0h(s)q(s)ds C 0 = e − r T ∫ 0 ∞ h ( s ) q ( s ) d s

下面公式提供了欧式期权的对应蒙特卡洛模拟公式，其中 SiT~ S T i ~ 是到期日期的第 i 个模拟指数水平。

公式 风险中立蒙特卡洛模拟公式

C0˜=e−rT1I∑i=1Ih(SiT~) C 0 ~ = e − r T 1 I ∑ i = 1 I h ( S T i ~ )

现在考虑几何布朗运动的参数化和估值函数gbm_mcs＿stat， 该函数仅以行权价格作为参数。 这里只模拟到期日的指数水平：

S0 = 100.
r = 0.05
sigma = 0.25
T = 1.0
I = 50000


def gbm_mcs_stat(K):
    """
    Valuation of European call option in Black-Scholes-Merton
    by Mont Carlo simulation ( of index level at maturity )
    :param k: float (positive) strike price of the option
    :return:
    """
    sn = gen_sn(1, I)
    # simulate index level at maturity
    ST = S0 * np.exp((r - 0.5 * sigma ** 2) * T + sigma * np.sqrt(T) * sn[1])
    # calculate payoff at maturity
    hT = np.maximum(ST - K, 0)
    # calculate MCS estimator
    C0 = np.exp(-r * T) * 1 / I * np.sum(hT)
    return C0

作为参考 ， 考虑行权价K=105的情况：

gbm_mcs_stat(K=105.)
# 9.9915714065433239

接下来 ， 我们考虑动态模拟方法 ， 除了看涨期权之外还可以模拟欧式看跌期权。 函数gbm_mcs_dyna 实现了这一算法：

M = 50


def gbm_mcs_dyna(K, option='call'):
    """
    Valuation of European option in Black-Scholes-Merton by Monte Carlo simulation(of index level paths)
    :param K: （positive）strike price of the option
    :param option:
    :return:
    """
    dt = T / M
    # simulation of index level paths
    S = np.zeros((M + 1, I))
    S[0] = S0
    sn = gen_sn(M, I)
    for t in range(1, M + 1):
        S[t] = S[t - 1] * np.exp((r - 0.5 * sigma ** 2) * dt + sigma * np.sqrt(dt) * sn[t])
    # case-based calculation of payoff
    if option == 'call':
        hT = np.maximum(S[-1] - K, 0)
    else:
        hT = np.maximum(K - S[-1], 0)
    # calculation of MCS estimator
    C0 = np.exp(-r * T) * 1 / I * np.sum(hT)
    return C0

# 比较相同行权价的看涨和看跌期权的价格估算
gbm_mcs_dyna(K=110.,option='call')
# 8.0198149275733481
gbm_mcs_dyna(K=110.,option='put')
# 12.619852239422888

问题是，这些基于模拟的估值方法与Black-Scholes-Merton 估值公式得出的基准值相比表现如何？为了找出这种差别，我们用BSM_Flncrions.py摸块中的Black-Scholes-Metron 分析性欧式看涨期权定价公式生成一定范围行权价的对应期权价值/估值：
bsm_functions.py

from bsm_functions import bsm_call_value

stat_res=[]
dyna_res=[]
anal_res=[]
k_list=np.arange(80.,120.1,5.)
np.random.seed(200000)
for K in k_list:
    stat_res.append(gbm_mcs_stat(K))
    dyna_res.append(gbm_mcs_dyna(K))
    anal_res.append(bsm_call_value(S0,K,T,r,sigma))

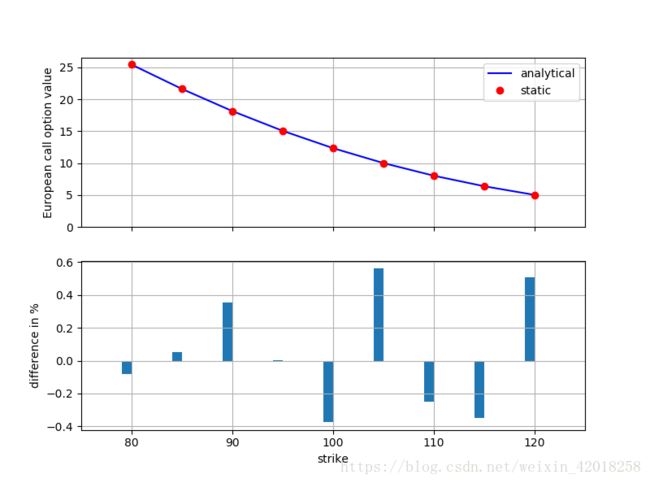
fig,(ax1,ax2)= plt.subplots(2,1,sharex=True,figsize=(8,6))
ax1.plot(k_list,anal_res,'b',label='analytical')
ax1.plot(k_list,stat_res,'ro',label='static')
ax1.set_ylabel('European call option value')
ax1.grid(True)
ax1.legend(loc=0)
ax1.set_ylim(ymin=0)
wi=1.0
ax2.bar(k_list-wi/2,(np.array(anal_res)-np.array(stat_res))/np.array(anal_res)*100,wi)
ax2.set_xlabel('strike')
ax2.set_ylabel('difference in %')
ax2.set_xlim(left=75,right=125)
ax2.grid(True)

fig,(ax1,ax2)= plt.subplots(2,1,sharex=True,figsize=(8,6))
ax1.plot(k_list,anal_res,'b',label='analytical')
ax1.plot(k_list,dyna_res,'ro',label='dynamic')
ax1.set_ylabel('European call option value')
ax1.grid(True)
ax1.legend(loc=0)
ax1.set_ylim(ymin=0)
wi=1.0
ax2.bar(k_list-wi/2,(np.array(anal_res)-np.array(dyna_res))/np.array(anal_res)*100,wi)
ax2.set_xlabel('strike')
ax2.set_ylabel('difference in %')
ax2.set_xlim(left=75,right=125)
ax2.grid(True)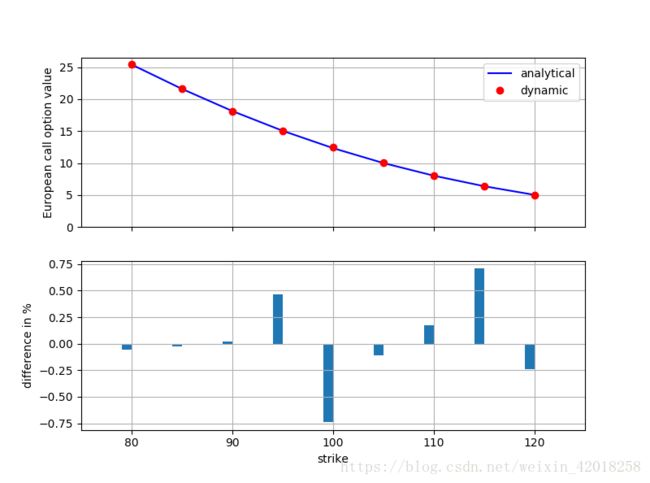

合并动态模拟和估值方法的类似图表， 可以得到上图的结果。同样，所有估值差异小于1% ， 标准差既有负数也有正数的情况。作为一般原则 ， 蒙特卡洛估算函数的质量可以通过调整使用的时间间隔 M 和模拟路径数 I 控制。

10.3.2 美式期权

美式期权的估值比欧式期权更复杂。在这种情况下， 必须解决最优截止问题，提出期权的公允价值。下面公式是将美式期权作为最优截止问题时的估值公式。该问题的公式化已经基于离散的时间网络， 以便用于数值化模拟。 在某种意义上， 更准确地说，这是百慕大式期权的估值公式。 时间间隔收敛干0长度时， 百慕大期权的价值收敛于美式期权的价值。

公式 以最优截止问题形式出现的美式期权价格

V0=supe−rTEQ0(hT(ST)) V 0 = s u p e − r T E 0 Q ( h T ( S T ) )

τ∈{0,Δt,2Δt,...,T} τ ∈ { 0 , Δ t , 2 Δ t , . . . , T }

下面描述的算法称为最小二乘蒙特卡洛（LSM）方法。由 Vt(s)=max(ht(s),Ct(s)) V t ( s ) = m a x ( h t ( s ) , C t ( s ) ) (其中 Ct(s)=EQt(e−rΔtVt+Δt(St+Δt)|St=s) C t ( s ) = E t Q ( e − r Δ t V t + Δ t ( S t + Δ t ) | S t = s ) ) 给出的任何给定日期 t 的美式（百慕大）期权价值是给定指数水平 St=s S t = s 下的期权持续价值。

现在我们考虑在 M 个等长 （ Δt Δ t ）的时间间隔中模拟指数水平的 I 条路径。 定义 Yt,i≡e−rΔtVt+Δt,i Y t , i ≡ e − r Δ t V t + Δ t , i 为路径 i 在时间 t 时的模拟持续价值。我们不能直接使用这个数字，因为它意味着完美的预期。但是，我们可以使用所有模拟持续价值的截面，通过最下二乘回归估算（预期）持续价值。

给定一组基函数 bd,d=1,...,D b d , d = 1 , . . . , D , 然后由回归估算公式 C^t,i=∑Dd=1α∗d,t⋅bd(St,i) C ^ t , i = ∑ d = 1 D α d , t ∗ ⋅ b d ( S t , i ) 算出持续价值，其中最优回归参数 α∗ α ∗ 是下面公式中最小二乘法问题的解。

公式 美式期权估值的最小二乘回归

minα1,t,...,αD,t1L∑d=1D(αd,t⋅bd(St,i))2 min α 1 , t , . . . , α D , t 1 L ∑ d = 1 D ( α d , t ⋅ b d ( S t , i ) ) 2

gbm_mcs_amer 函数实现美式看涨和看跌期权的LSM 算法：

def gbm_mcs_amer(K, option='call'):
    """
    Valuation of American option in Black-Scholes-Merton
    by Monte Carlo simulation by LSM algorithm
    :param K: (positive) strike price of the option
    :param option: type of the option to be valued ('call','put')
    :return: estimated present value of American call option
    """
    dt = T / M
    df = np.exp(-r * dt)
    # simulation of index levels
    S = np.zeros((M + 1, I))
    S[0] = S0
    sn = gen_sn(M, I)
    for t in range(1, M + 1):
        S[t] = S[t - 1] * np.exp((r - 0.5 * sigma ** 2) * dt
                                 + sigma * np.sqrt(dt) * sn[t])
    # case-based calculation of payoff
    if option == 'call':
        h = np.maximum(S - K, 0)
    else:
        h = np.maximum(K - S, 0)
    # LSM algorithm
    V = np.copy(h)
    for t in range(M - 1, 0, -1):
        reg = np.polyfit(S[t], V[t + 1] * df, 7)
        C = np.polyval(reg, S[t])
        V[t] = np.where(C > h[t], V[t + 1] * df, h[t])
    # MSC estimator
    C0 = df * 1 / I * np.sum(V[1])
    return C0

gbm_mcs_amer(110.,option='call')
# 7.8552809171254045
gbm_mcs_amer(110.,option='put')
# 13.646476865931355

欧式期权的价值处于美式期权价值的下界。 两者的差异通常称作提前行权溢价。 下面，我们比较和以前相同的行权价范围内的欧式和美式期权价值， 以估算期权溢价。 这次我们选择看跌期权：

euro_res = []
amer_res =[]
k_list = np.arange(80., 120.1, 5.)
for K in k_list:
    euro_res.append(gbm_mcs_dyna(K,'put'))
    amer_res.append(gbm_mcs_amer(K,'put'))
euro_res = np.array(euro_res)
amer_res = np.array(amer_res)

fig, (ax1 ,ax2) = plt.subplots(2, 1, sharex=True, figsize=(8, 6))
ax1. plot(k_list, euro_res,'b', label='European put')
ax1. plot(k_list, amer_res,'ro',label='American put')
ax1.set_ylabel('call option value')
ax1.grid(True)
ax1.legend(loc=0)
wi = 1.0
ax2.bar(k_list - wi / 2, (amer_res - euro_res) / euro_res * 100, wi)
ax2.set_xlabel('strike')
ax2.set_ylabel('early exercise premium in %')
ax2.set_xlim(left=75, right=125)
ax2.grid(True)

欧式期权和LSM蒙特卡洛估算值的对比

未完待续……