《算法笔记》—— 图 "邻接矩阵" 的遍历(DFS、BFS)
去年了解了一下图,过去了那么长的时间没有学习算法,算法还是很重要的,重新学习吧 ~
此文知识点相关文章
与数据结构 —— 图相关的文章有:
初探数据结构 —— 图 (邻接矩阵实现)
初探数据结构 —— 图 (邻接表实现)与DFS、BFS相关的文章有:
《算法笔记》—— “迷宫求解” 之 深度优先搜索(DFS)
《算法笔记》—— “迷宫求解” 之广度优先搜索(BFS)
文章目录
- 图 —— 邻接矩阵
- DFS遍历原理
- BFS遍历原理
- DFS遍历邻接矩阵源码讲解
- BFS遍历邻接矩阵源码讲解
- 十字总结
.
图 —— 邻接矩阵
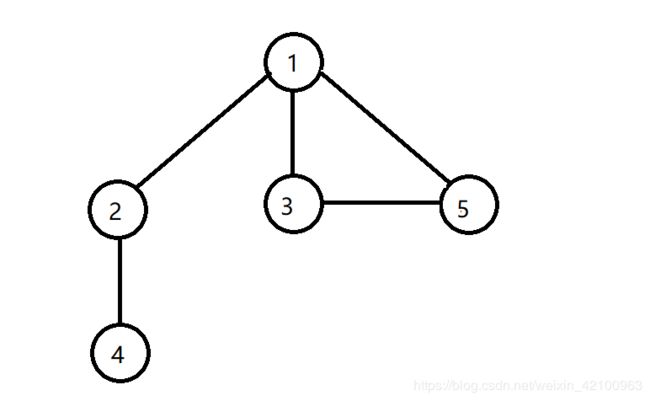
学习前面的两篇《算法笔记》 —— 深度搜索(DFS)、广度搜索(BFS),我们会想到一个问题,那就是这两种搜索为什么叫这个名字呢 ? 其实这都是针对数据结构 —— 图而言的,那么图是什么东西呢?例如下图所示:
所谓什么是图,其实是由一些点通过线连接组合而成。上面的五个点,每个点与其它的点(有 / 没有)联系 . . .
更加深层的概念此处就不再讲解,回到我们的主题 —— 邻接矩阵的搜索,邻接矩阵是什么东西,在我去年写过的文章中有讲,开头以给出链接,所谓 邻接矩阵其实就是图的点与线的存储方式 而已,此处可以看一下我用C++写的邻接矩阵文章:
对图的数据进行存储,除了邻接矩阵,实则还有一个 邻接表 存储,有兴趣的小伙伴可以观看一波,顺便点个赞 ^ _ ^,我爱你们 . . .
下面我们用 DFS、BFS来完成对邻接矩阵的搜索,我们先来探讨一下他们是怎样的探索,最后我们将以源码来实现他们 . . .
.
DFS遍历原理
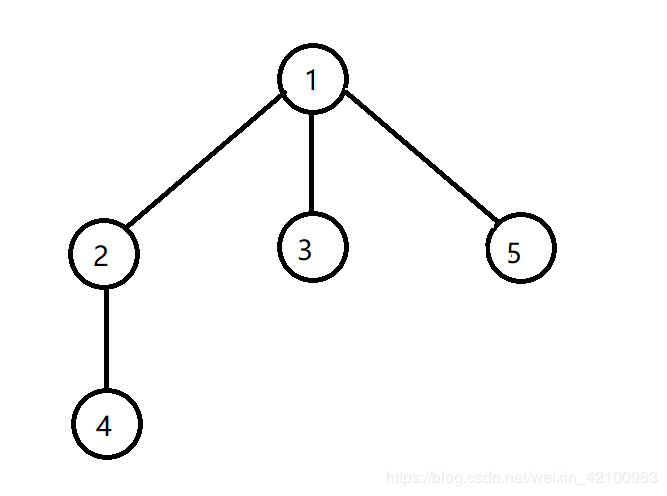
利用DFS对图的遍历,是基于某一点进行的,例如我们从1号顶点开始遍历这个图,将每一个顶点都访问一次,我们使用DFS来遍历这个图结果如下所示:
利用DFS遍历,难免会想到栈、递归的原理,下面我简要的说明一下遍历的过程:
首先以
顶点1为起点,访问顶点2(没有被访问过),接着访问顶点5(没有被访问过),顶点5下面没有与这关联的顶点,返回顶点2,顶点2下面的顶点5被访问过,返回顶点1,顶点1下面的顶点2被访问过,接着访问顶点3,和上面一样的方式访问顶点4,然后访问结束 . . .
.
所以依次遍历的结果为:1 —— 2 —— 5 —— 3 —— 4
遍历的过程也是和DFS原理相对应,可能上面讲的过程比较抽象,但本质并没有变化,讲解一下深度优先遍历的主要的思想:首先以一个未被访问过的顶点作为起始顶点,沿当前顶点的边直到未访问过的顶点;当没有未访问过的顶点时,则回到上一个顶点,继续试探访问别的顶点,直到所有的顶点都被访问过,显然这是一种回溯法 . . .
上面的红色字体完美说出了DFS的工作过程 . . .
.
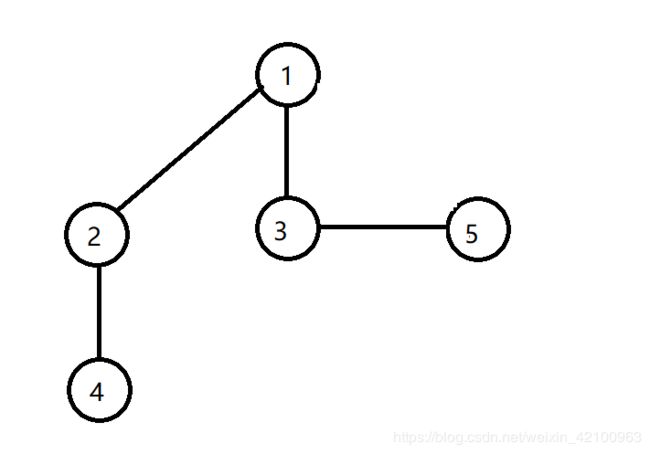
BFS遍历原理
BFS遍历方式是将某一点放入队列之中,然后将与他相关联的顶点也放入队列之中,然后队列头部后移,继续完成上面的操作,直至所以顶点都被遍历完成 . . .
所以依次遍历的结果为:
1 —— 2 —— 3 —— 5 —— 4
他的队列操作原理图如下:
首先我们以顶点1为队头,然后将图中与顶点1相连的顶点依次放入队列之中,然后我们以顶点2为队头,将图中与顶点2 相连的顶点放入队列之中,反复如此,直至所有顶点都遍历完成 . . .
.
DFS遍历邻接矩阵源码讲解
将分解的每一个小思路转化为代码,让我们理解的更加清楚
- 标记数组(用于标记顶点是否被访问过)、访问过的顶点个数(用于终止dfs方法):
int flag[5], sum;- 邻接矩阵:
int e[5][5] = {
0,1,1,3,1,
1,0,3,1,3,
1,3,0,3,1,
3,1,3,0,3,
1,3,1,3,0
};
0 表示自己、3表示没有连接、1表示有连接关系
- DFS遍历:
void dfs(int cur)
{
printf("%d ", cur+1); // 输出当前的顶点(因为从0开始,所以 + 1)
++sum; // 统计被访问的顶点个数
if(sum == 5) // 全部访问完成终止dfs函数
return;
int i;
for(i = 0; i < 5; ++i) // 每个顶点有五种的可能性
{
// 判断当前顶点与其它顶点是否有联系(并且其它顶点没有被访问过)
if(e[cur][i] == 1 && flag[i] == 0)
{
flag[i] = 1; // 与当前顶点有联系的顶点标记为以访问
dfs(i); // 递归与之有联系的顶点
}
}
}每一行代码我都以讲清楚了
- 调用dfs:
flag[0] = 1; // 第一个顶点标记为以访问
dfs(0); // 开始进行dfs完整的源码此处就不展示了,我们只需要将第4点的两行代码放入到主函数 main中即可
运行结果如下所示:
1 2 4 3 5
.
BFS遍历邻接矩阵源码讲解
- 声明队列、头部与尾部索引下标:
int queue[5];
int head, tail;- 标记数组与邻接矩阵:
int book[5];
int e[5][5] = {
0,1,1,3,1,
1,0,3,1,0,
1,3,0,3,1,
3,1,3,0,3,
1,3,1,3,0
};- bfs遍历:
void bfs()
{
while(head < tail) // 队头索引小于尾部索引
{
int cur = queue[head]; // 获取队头的顶点
int i = 0;
for(; i < 5; i++) // 五种可能性
{
if(e[cur][i] == 1 && book[i] == 0) // 判断是否满足条件
{
book[i] = 1;
queue[tail++] = i; // 顶点加入队列
}
if(tail > 5) // 判断是否已经访问完成,避免性能的浪费
break;
}
++head; // 一个顶点访问完成,换成下一个顶点反复访问
}
}- 初始化队列:
queue[head] = 0;
++tail;
book[0] = 1;- 执行 bfs、输出结果:
bfs();
int i;
for(i = 0; i < 5; i++)
printf("%d ", queue[i] + 1);结果输出如下所示:
1 2 3 5 4
.
十字总结
DFS以当前点为核心、BFS以队列中的head为核心 . . .
.
作者:浪子花梦