python机器学习 第二章（1.感知器的训练与测试）

2.1.1人工神经元的正式定义

如果把人工神经元逻辑运用在二元分类场景，将两个类分别名命为正类（1）和负类（-1）以简化操作。定义决策函数Φ（z） z=w1x1+…wmxm作为净输入。

令w0=-θ，x0=1则有：

z=w0x0+…+wmxm=wTx

当z≥0时，决策函数为1，反之为-1 一般将w0叫做偏置。

2.1.2MCP神经元和感知器模型

背后的原理即：达到一定的条件就会触发，否则不触发。初始感知器规则可以总结为以下几步：

1.把权重初始化为0或更小的随机数

2.对每个训练样本xi：

a.计算输出值y(估计)

b.更新权重

每一个权重的更新规则是：学习率（0-1）预测值与真实值之差与那个权重对应的特征值。

总的来说，一个感知器以一组特征值与对应每个特征值的乘积的和为输入。每一组输入代表一个样本。最开始我们是不知道每个特征的权重是占多少的，即，我们不知道样本的各个特征作为样本分类依据的比重是多少。经过一次输入后，我们通过与已知的结果标签对比，通过修正公式得到新的权重。多次后，这个权重向量就能大概被确定下来，即，大概知晓每个特征在分类时作为依据的可信度为多少。得到了这个权重后，我们就可以利用它预测拥有一组特征的样本的标签（种类）。整体流程如下

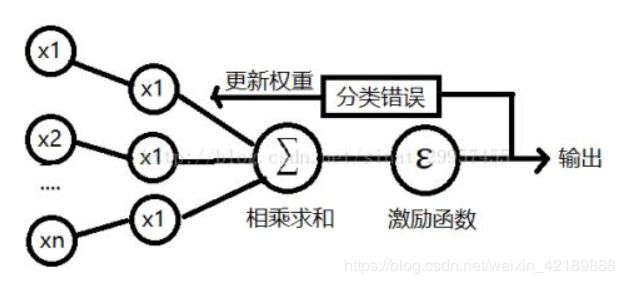
2.2用python实现感知器学习算法+注释：

 import numpy as np
    
    class Perceptron(object):
        """Perceptron classifier.
    
    Paramenters
    ------------
    eta:float
      Learning rate (between 0.0 and 1.0)
    n_iter:int
      passes over the training dataset
    random_state:int
      Random number generator seed for random weight
      initialization.
      
    Attributes
    ------------
    w_:1d-array
      weight after fitting
    errors_:list
      Number of misclassifications(updates)in each epoch
      
      
    """
    def __init__(self,eta=0.01,n_iter=50,random_state=1):#初始化，指定学习率，训练次数和用于初始权重的随机数种子。
        self.eta=eta
        self.n_iter=n_iter
        self.random_state=random_state
    
    def fit(self,X,y):
        """Fit training data
        
        Paramenters
        ------------
        X:{array-like},shape=[n_samples,n_features]
         Training vectors,where n_samples is the number of
         samples and 
         n_features is the number of the features.
        y:array-like,shape=[n_samples]
         Target values
         
        Returns
        -------
        self:object
        
        """
        rgen=np.random.RandomState(self.random_state)
        self.w_=rgen.normal(loc=0.0,scale=0.01,size=1+X.shape[1])#指定权重是以0为均值，0.01为标准差的正态分布，规模是X的列数（样品特征数）+1 加一是因为有一个偏置
        self.errors_=[]
        
        for _ in range(self.n_iter):#表示即将进行n_iter次循环，n_iter已经设定好了是训练次数
            errors=0
            for xi,target in zip(X,y):#xi表示一个数组，这个数组存放每一个样本的所有特征。y存放标签，表示每一个样本真实的标签
                update=self.eta*(target-self.predict(xi))#根据公式算出每一个样本的权重更新值，注意这里update应该是一个数组
                self.w_[1:]+=update*xi#将更新与原权重相加，注意w0是偏置，直接加update，不用乘以xi
                self.w_[0]+=update
                errors+=int(update!=0.0)#errors记录当前样本是否预测正确
            self.errors_.append(errors)#记录每一次训练后错误数量的大小
        return self
    
    def net_input(self,X):
        """Calculate net input"""
        return np.dot(X,self.w_[1:])+self.w_[0]#返回输入：样本的每个权重*特征值
    
    def predict(self,X):#预测函数，根据公式，如果乘积之和大于等于零为1类，反之为-1类
        """Return class label after unit step"""
        return np.where(self.net_input(X)>=0.0,1,-1)

下面利用鸢尾花数据集，检验我们的感知器模型效果：

1.用pandas库的read_csv()方法读取数据集，输出后五行检查数据是否成功加载

2.下面的代码提取前100个样本，以其中两个特征为例，用matplotlib.pyplot，显示它们的真实分类情况

import matplotlib.pyplot as plt
import numpy as np

y=df.iloc[0:100,4]#选取数据集中0到99行的第四列（第五列）数据
y=np.where(y=='Iris-setosa',-1,1)#将真实标签1 -1化

X=df.iloc[0:100,[0,2]].values#注意这里必须要获取values以获得相应的二维数组

plt.scatter(X[:50,0],X[:50,1],color='red',marker='o',label='setosa')#绘制前50个数据的二维特征图像
plt.scatter(X[50:100,0],X[50:100,1],color='blue',marker='x',label='versicolor')#绘制后50个数据的二维特征图像
plt.xlabel('sepal length [cm]')
plt.ylabel('petal length [cm]')#指定标签
plt.legend(loc='upper left')#添加图例
plt.show()

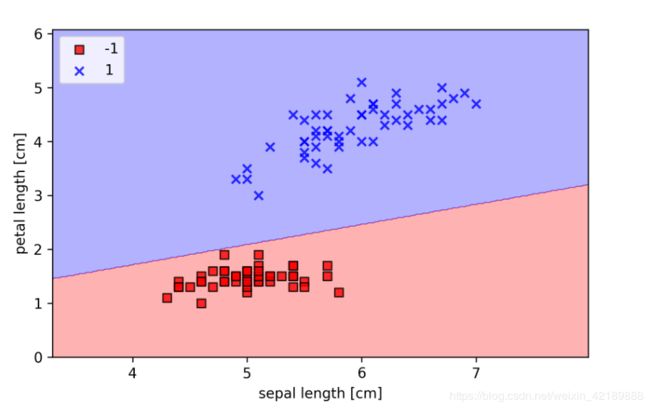
可以看到，两者之间可以用一条直线分开，说明可以用一个线性决策边界将两种类型的花分开

3.以下代码执行训练，并且展示分类错误的数量随分类次数变化的情况：

ppn = Perceptron(eta=0.1,n_iter=10)

ppn.fit(X, y)

plt.plot(range(1, len(ppn.errors_) + 1), ppn.errors_, marker='o')
plt.xlabel('Epochs')
plt.ylabel('Number of updates')

plt.show()

4.训练完毕，接下来将分类边界可视化：

from matplotlib.colors import ListedColormap
import numpy as np

def plot_decision_regious(X,y,classifier,resolution=0.02):
    markers=('s','x','o','^','v')
    colors=('red','blue','lightgreen','gray','cyan')
    cmap=ListedColormap(colors[:len(np.unique(y))])
    
    x1_min,x1.max=X[:,0].min()-1,X[:,0].max()+1
    x2_min,x2.max=X[:,1].min()-1,X[:,1].max()+1
    xx1,xx2=np.meshgrid(np.arange（x1_min,x1_max,resolution）,
                        np.arange(x2_min,x2_max,resolution))
    Z=classifier.predict(np.array([xx1.ravel(),xx2.ravel()]).T)
    Z=Z.reshape(xx1.shape)
    plt.contourf(xx1,xx2,Z,alpha=0.3,cmap=cmap)
    plt.xlim(xx1.min(),xx1.max())
    plt.ylim(xx2.min(),xx2.max())
    
    for idx,cl in enumerate(np.unique(y)):
        plt.scatter(x=X[y==cl,0],
                    y=X[y==cl,1],
                   alpha=0.8,
                   c=colors[idx],
                   marker=markers[idx],
                   label=cl,
                   edgecolor='black')