最小生成树-Kruskal算法-python
图的基本概念:
- 图:图由顶点集V和边集E组成,表示为G=(V,E);
- 边权:边e具有权重,(结合不同环境具体可以理解为两点的距离、相似度)
- 树:任意两点都有路径相连,但是没有回路
- 最小生成树(MST:minimum spanning tree):边权之和最小的树,n个顶点产生(n-1)个边
Kruskal算法原理:
- 将边按权重从小到大进行排序;
- 将每个顶点独立视为根节点,产生n个树;
- 依次选取每条边,如果边的两个顶点不属于同一个树,则将其合并,如果属于同一个树(意味着会形成回路),则将其舍弃,考虑下一条边,最后形成(n-1)条边
Kruskal算法解析
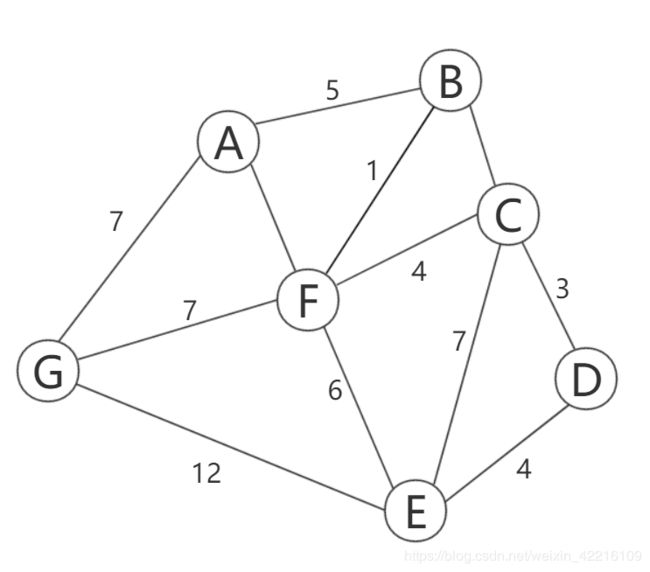
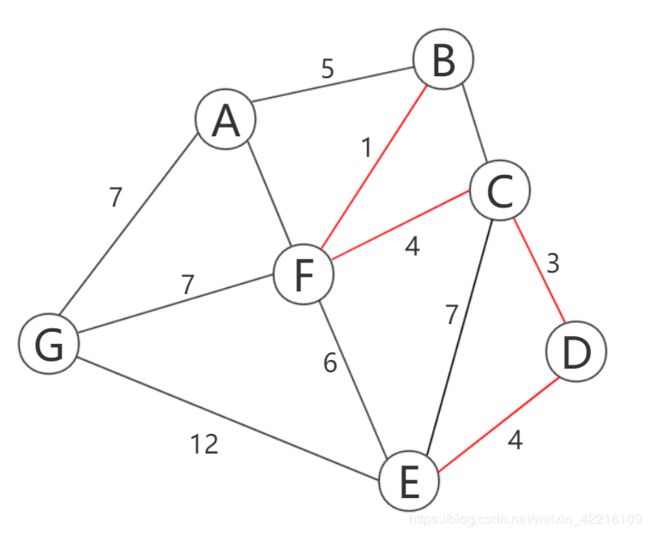
图1由顶点集{‘A’,‘B’,‘C’,‘D’,‘E’,‘F’,‘G’}和一系列带有权重的边组成(本质上n个顶点两两相连可以形成n(n-1)/2条边,图中省略部分边及边权)
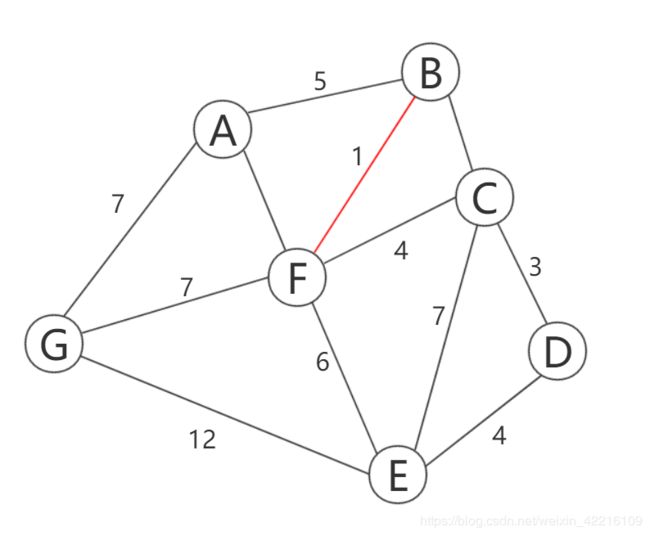
将7个顶点视为7个树的根节点。首先选取权重最小的边e(BF),其顶点为B、F,两点不属于同一棵树,故合并。
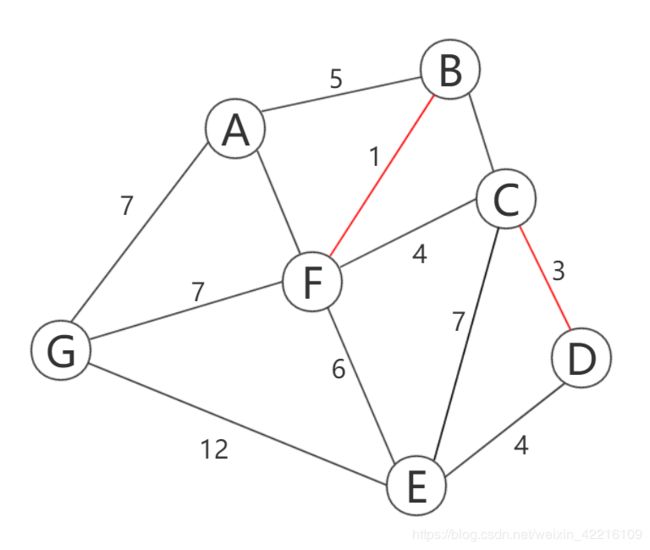
然后选取权重为3的边e(CD),两点也不属于同一棵树,故合并。
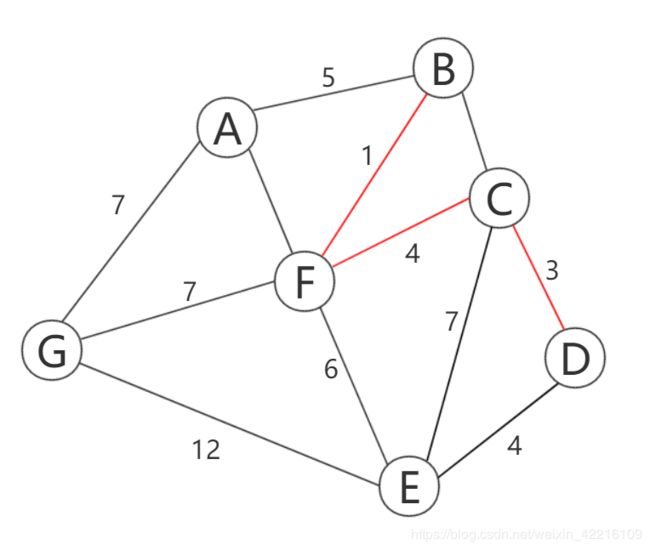
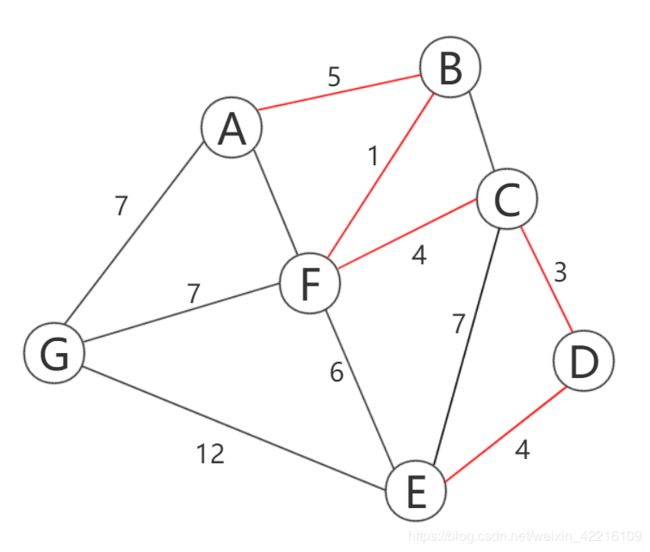
重复上述步骤,依此得到:
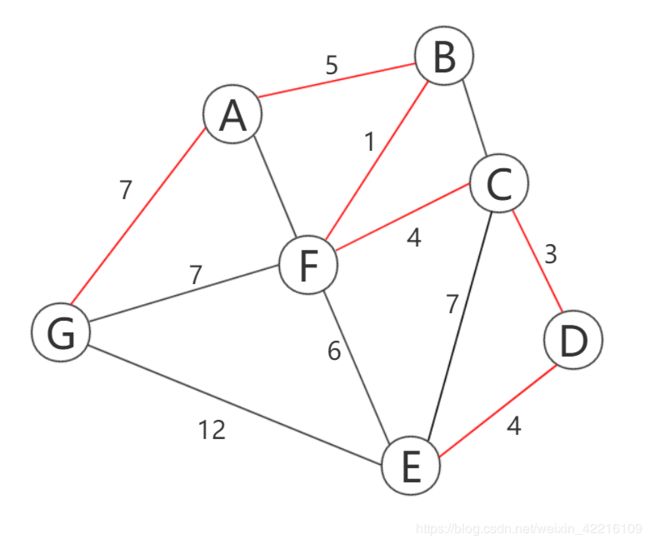
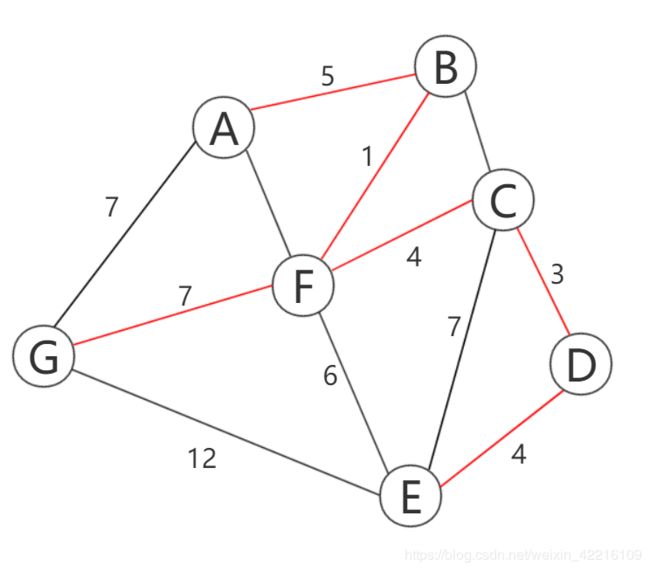
当选取到权重为6的边e(EF)时,发现顶点E,F同属于一棵树,故舍弃,最后最小生成树有两种情况,如图7,图8
实操
1.定义顶点
vertices=list('ABCDEFG')2.定义边并按边权进行排序
edges = [("A", "B", 5), ("A", "G", 7),
("B", "F", 1), ("C", "F", 4),
("C", "D", 3), ("C", "E", 7),
("E", "F", 6), ("D", "E", 4),
("E", "G", 12),("F", "G", 12)]
edges.sort(key=lambda x:x[2])
print(edges)输出如下:
3.将每个顶点视为一棵节点树,可以用字典表示,键表示顶点,键值表示顶点所在树的节点
ori_trees=dict()
for i in vertices:
ori_trees[i]=i
print(ori_trees)输出为:
4.根据边的两个顶点的根节点是否相同考虑是否合并
#寻找根节点
def find_node(x):
if ori_trees[x]!=x:
ori_trees[x]=find_node(ori_trees[x])
return ori_trees[x]
#定义最小生成树
mst=[]
#定义循环次数,n为需要添加的边数=顶点数-1
n=len(vertices)-1
#循环
for edge in edges:
v1,v2,_=edge
if find_node(v1)!=find_node(v2):
ori_trees[find_node(v2)]=find_node(v1)
mst.append(edge)
print('添加第'+str(7-n)+'条边后:')
n-=1
print(ori_trees)
print(mst)
if n==0:
break输出结果如下:
完整代码如下:
edges = [("A", "B", 5), ("A", "G", 7),
("B", "F", 1), ("C", "F", 4),
("C", "D", 3), ("C", "E", 7),
("E", "F", 6), ("D", "E", 4),
("E", "G", 12),("F", "G", 12)]
vertices=list('ABCDEFG')
edges.sort(key=lambda x:x[2])
ori_trees=dict()
for i in vertices:
ori_trees[i]=i
#寻找根节点
def find_node(x):
if ori_trees[x]!=x:
ori_trees[x]=find_node(ori_trees[x])
return ori_trees[x]
#定义最小生成树
mst=[]
#定义循环次数,n为需要添加的边数=顶点数-1
n=len(vertices)-1
#循环
for edge in edges:
v1,v2,_=edge
if find_node(v1)!=find_node(v2):
ori_trees[find_node(v2)]=find_node(v1)
mst.append(edge)
print('添加第'+str(7-n)+'条边后:')
n-=1
print(ori_trees)
print(mst)
if n==0:
break