Leetcode刷题|面试题 16.03. 交点
今天早上起晚了,没有赶上leetcode的周赛,后面一个人默默赛外刷完了。没什么可讲的,除了最后一题用了Ctrl+c+v其他都还算简单。到晚上又想起今天忘了写每日一题,遂又埋头苦战,困难题诚不欺我,着实是花了我一个多小时(链接)。
现在来讲一下这题和这题的思路。
给定两条线段(表示为起点start = {X1, Y1}和终点end = {X2, Y2}),如果它们有交点,请计算其交点,没有交点则返回空值。
要求浮点型误差不超过10^-6。若有多个交点(线段重叠)则返回 X 值最小的点,X 坐标相同则返回 Y 值最小的点。
示例 1:
输入:
line1 = {0, 0}, {1, 0}
line2 = {1, 1}, {0, -1}
输出: {0.5, 0}
示例 2:
输入:
line1 = {0, 0}, {3, 3}
line2 = {1, 1}, {2, 2}
输出: {1, 1}
示例 3:
输入:
line1 = {0, 0}, {1, 1}
line2 = {1, 0}, {2, 1}
输出: {},两条线段没有交点
提示:
坐标绝对值不会超过 2^7
输入的坐标均是有效的二维坐标
其实这题不算难,就是太费事了。思路也很简单,简而言之,其实就是我们小学的判断两个线段是否相交,用笔算挺简单,没想到写成代码这么费事。那已知小学数学题的情况下,有两条线段a和b:
-
我们肯定要判断两个线段的斜率是否存在:一.a存在b不存在(b存在a不存在)。二.a和b都不存在。三.a和b都存在。
-
在条件一下,我们得到的直线应该形如下图:
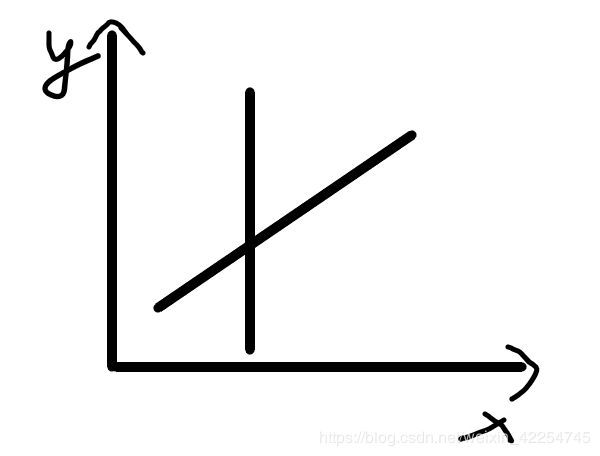
或者:
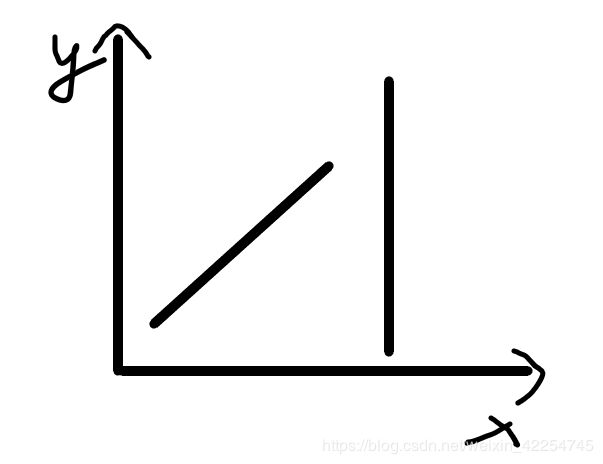
那我们的做法就是先判断斜线的起始x坐标是否包含竖线的x坐标,如果不满足,直接返回null。如果满足,将竖线的横坐标带入斜线的方程,看得到的y值是否在竖线范围内,如果是,就返回这个交点。 -
在条件二下,我们可能会得到这样的线段:
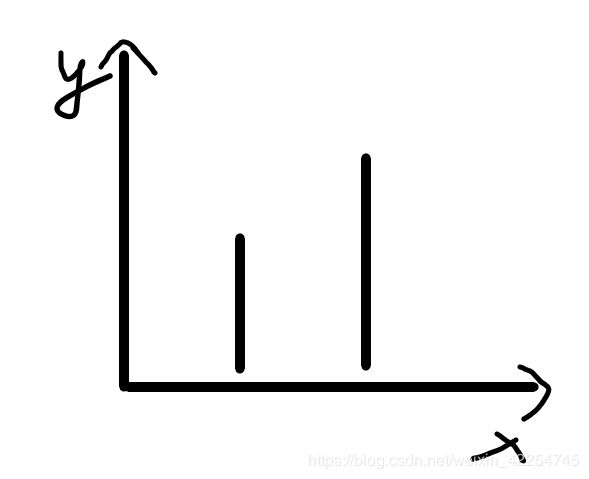
或者:
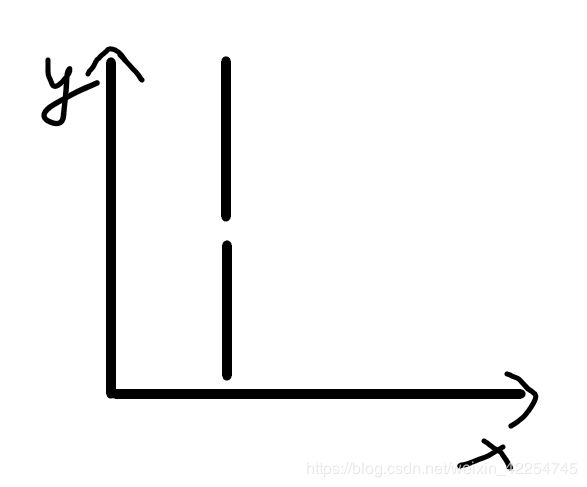
那我们的做法就是先判断二者竖线的x坐标是否一致,如果不一致,直接返回null。如果一致,判断二者是否有重合部分:一个线段的两个端点是否在另外一个线段的范围内,只要有一个端点满足就可以。如果有重合部分,那么根据规则我们返回四个端点中y值第二大的点坐标。 -
条件三下就比较简单了,同样可能产生如下情况:
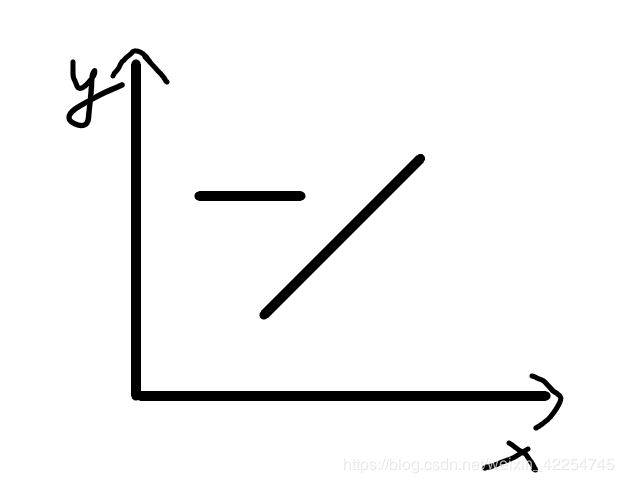
或者:
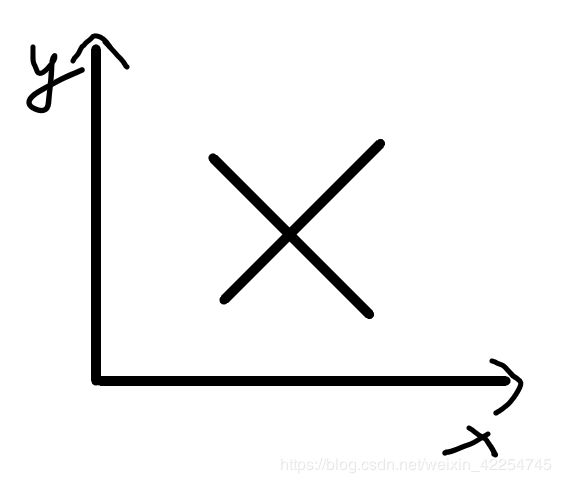
两条直线都有斜率且不平行那肯定有交点。那我们要做的就是判断得到的交点是否在两条线段的范围内。判断方法如下:
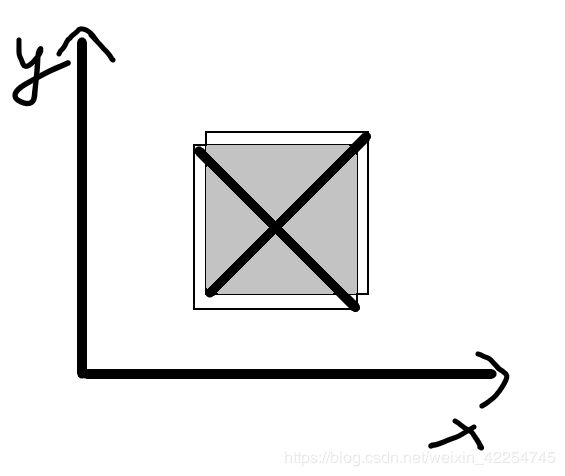
即我们只需要判断焦点是否在两条线段交集的范围内。
到这里这题就解决了,分析方法还是简单的,就是分类讨论,主要就是考虑一定得全面。
下面贴上我的代码,python渣渣,写的比较乱,凑合看。
class Solution:
def intersection(self, start1: List[int], end1: List[int], start2: List[int], end2: List[int]) -> List[float]:
if start1[0]==end1[0] or start2[0]==end2[0]:#条件一+条件二
if start2[0]!=end2[0]:#条件一
if min(start2[0],end2[0])<=start1[0]<=max(start2[0],end2[0]):
k=(start2[1]-end2[1])/(start2[0]-end2[0])
b=start2[1]-(start2[1]-end2[1])/(start2[0]-end2[0])*start2[0]
if min(start1[1],end1[1])<=k*start1[0]+b<=max(start1[1],end1[1]):
return [start1[0],k*start1[0]+b]
else:
return {}
else:return {}
elif start1[0]!=end1[0]:#条件一
if min(start1[0],end1[0])<=start2[0]<=max(start1[0],end1[0]):
k=(start1[1]-end1[1])/(start1[0]-end1[0])
b=start1[1]-(start1[1]-end1[1])/(start1[0]-end1[0])*start1[0]
if min(start2[1],end2[1])<=k*start2[0]+b<=max(start2[1],end2[1]):
return [start2[0],k*start2[0]+b]
else:
return {}
else:return {}
else:#条件二
if start1[0]==start2[0]:
if min(start2[1],end2[1])<=start1[1]<=max(start2[1],end2[1]) or min(start2[1],end2[1])<=end1[1]<=max(start2[1],end2[1]):
return [start1[0],sorted([start1[1],end1[1],start2[1],end2[1]])[1]]
else:
return {}
else:
return {}
else:#条件三
k1=(start1[1]-end1[1])/(start1[0]-end1[0])
b1=start1[1]-(start1[1]-end1[1])/(start1[0]-end1[0])*start1[0]
k2=(start2[1]-end2[1])/(start2[0]-end2[0])
b2=start2[1]-(start2[1]-end2[1])/(start2[0]-end2[0])*start2[0]
if k1==k2:
if b1==b2:
jiao_x = sorted([start1[0],end1[0],start2[0],end2[0]])[1]
jiao_y = k1*jiao_x+b1
if min(start1[0],end1[0])<=jiao_x<=max(start1[0],end1[0]) and min(start2[0],end2[0])<=jiao_x<=max(start2[0],end2[0]) and min(start1[1],end1[1])<=jiao_y<=max(start1[1],end1[1]) and min(start2[1],end2[1])<=jiao_y<=max(start2[1],end2[1]):
return [jiao_x,jiao_y]
else:
return {}
else:
return {}
else:
jiao_x = (b2-b1)/(k1-k2)
jiao_y = k1*jiao_x+b1
if min(start1[0],end1[0])<=jiao_x<=max(start1[0],end1[0]) and min(start2[0],end2[0])<=jiao_x<=max(start2[0],end2[0]) and min(start1[1],end1[1])<=jiao_y<=max(start1[1],end1[1]) and min(start2[1],end2[1])<=jiao_y<=max(start2[1],end2[1]):
return [jiao_x,jiao_y]
else:
return {}
