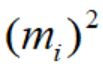VAE(Variational Autoencoder)的通俗理解和理论推导
VAE(Variational Autoencoder)是AE(Autoencoder)的一种改进，属于无监督学习的范畴。本文从感性认识和理论推导两部分来阐述VAE,并总结VAE的优点以及其缺点。
- 感性认识VAE(1.1 什么是AE ; 1.2 感性认识VAE ; 1.3 Why VAE)
- 理论推导VAE(2.1 高斯混合模型 ；2.2 VAE的理论推导)
- VAE的缺点
一.感性认识VAE
1.1 什么是AE(Auto-encoder)
一张图解释什么是AE：
图1：AE的感性理解
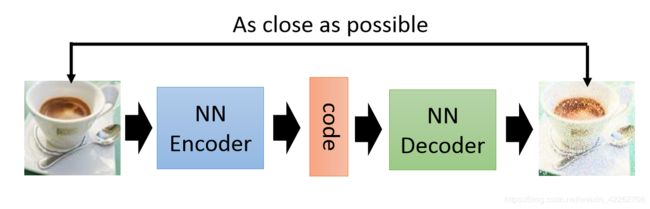
如图1所示：现网络输入的是一张图片X,经过NN Encoder(神经网络编码器)之后输出图片编码为code,为了使编码code能够很好的表示输入的图片X，现将编码经过NN Decoder(神经网络解码器)之后复原图像，要求复原的图片和输入的图片尽可能相似(即通过损失函数来衡量)，从而调节网络中的参数。
图2：code解码
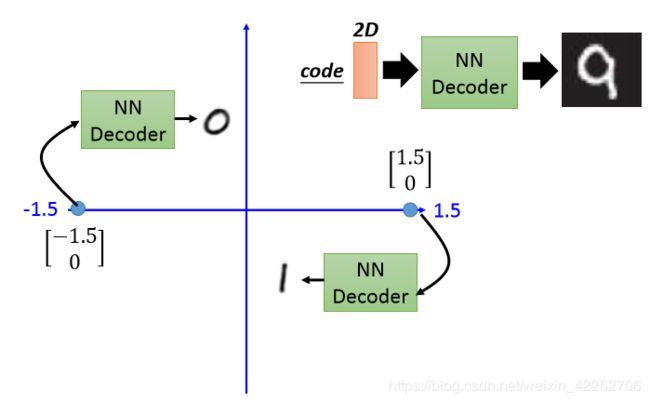
如图2所示，假设手写数字图片经过NN Encoder之后code的维度为2(其实就是一个降维的过程)，再将code再经过NN Decoder复原原图像。如code为[-1.5,0]时，复原的数字为0；[1.5,0]复原为1，其余情况如图3所示。
图3：code解码
1.2 感性认识VAE
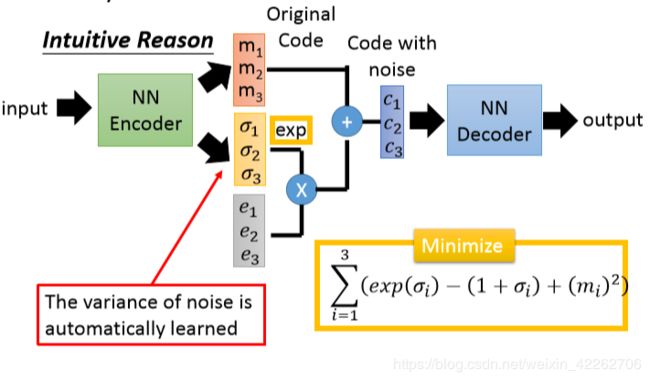
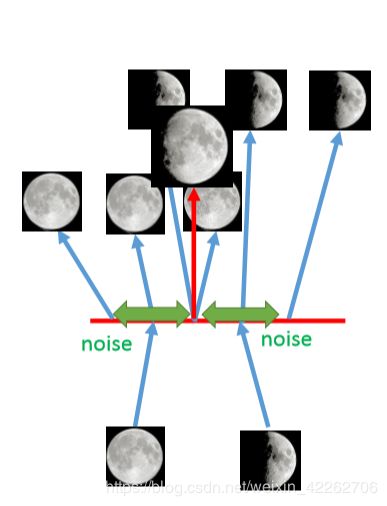
VAE的实质其实还是AE，只不过在NN Encoder过程中加了一点小变动。VAE与AE的不同点可以从图4中看出，主要就是VAE对code进行了一些调整，即将原先的code加上了噪声，从使得整个网络的鲁棒性更高。其中[e1,e2,e3]采样于正态分布。
图4：VAE
在网络的训练过程中，不仅要最小化重建误差，即要求输入图片和重建图片越相似越好，还要最小化图5的式子
图5：最小化式子
至于为什么要最小化图5的式子，直观的解释如下：
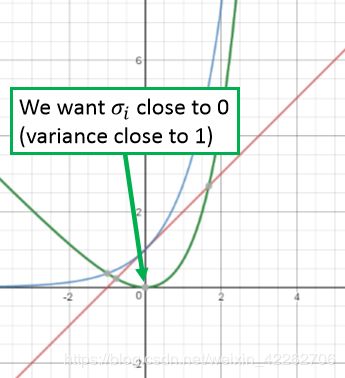
如果仅仅最小化重建误差，在训练的过程中，引入的噪声方差将会为0.在最小化图5的时候，可以保证误差的方差最小为1.图6中蓝色的线为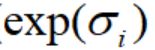
,红色的线为
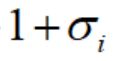，绿色的线为
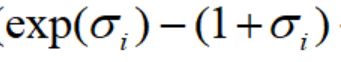。可以看出绿色曲线的最小值为0，此时
=0，噪声方差为1.(噪声为
)
可以看成是L2正则项，防止过拟合。
图6：直观解释最小化
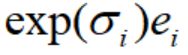1.3 Why VAE
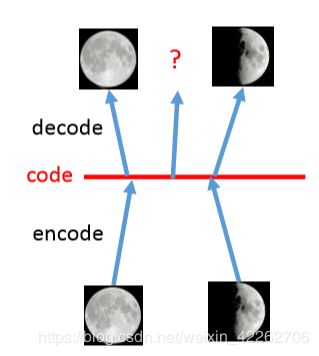
一张图直观解释为什么VAE比AE效果好： 左图为传统的AE,假设一张满月照经过encode变成一维的code,然后再将code经过decode重建为原来的图像，同理将弦月照经过同样的过程。但是在code space中(即红线部分)，位于满月和弦月之间的code不知要重建成什么样的图片；在VAE中，将满月的code和弦月的code都加上了噪声，所以处于中间的部分在进行重建时，既要像满月又要像弦月，因此重建成介于满月和弦月之间的图片。
图7 直观理解VAE
二.理论推导VAE
2.1高斯混合模型(Gaussian Mixture Model)
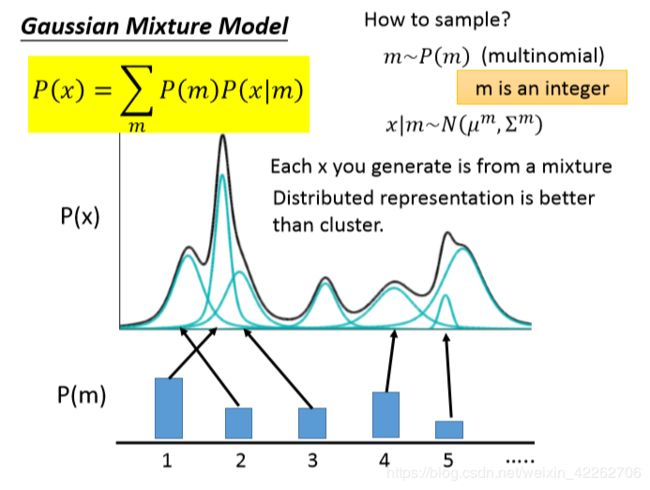
为了估计一个不规则的概率分布P(X),这里假设x为1维数据，对于每一个样本x而言(如x1),p(x1)=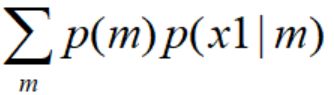
,每一个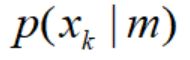
均服从高斯分布，最后通过最大似然估计(
)估计出每一个高斯分布的均值和方差。
求出每一个高斯分布的均值和方差后，P(X)=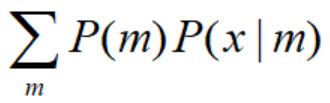
，如图中的黑色曲线；
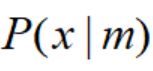为图中的蓝绿色曲线。
其实，高斯混合模型就是用多个不同的高斯函数加权去拟合一个未知的概率分布。具体每一个高斯分布的均值和方差要如何计算，参加EM(期望最大化)算法。
图8 高斯混合模型
2.2VAE推导
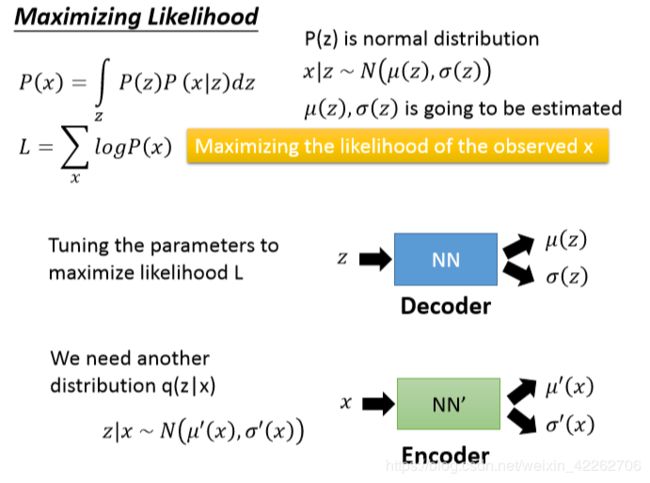
如图9所示，z是一组向量，从正态分布中sample,z的每一个维度都代表了一种属性。(z其实就是x经过降维之后的输出)，z的每一个属性的分布均服从高维高斯分布。现根据z的每一个属性的高维高斯分布来拟合X的真实分布。(其实就是一个Decoder的过程，根据低维特征重构原始图像)。
图9
如图10所示，对于每一个样本均有一个p(x),因此对于所有的样本可以构建最大似然函数L,现在的目的就是最大化似然函数。通过Decoder 神经网络不断调整其内部参数，改变z的每一属性对应的高维高斯函数的期望与方差，从而最大化似然函数。
图10
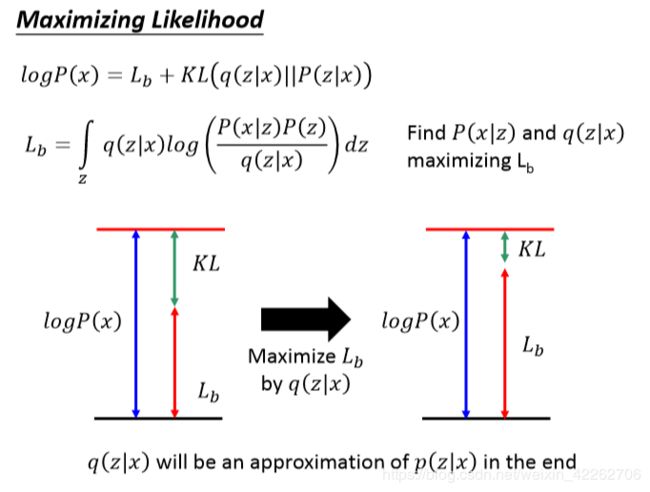
如图11所示：其中q(z|x)的含义是，给定一个输入x，决定编码器输出z是从什么样的期望和方差中sample得到。通过最大化似然函数，引入q(z|x),推导过程如图11.似然函数的下界为lower bound Lb
图11
如图12所示，最大化似然函数简化成最大化Lb,即寻找p(x|z)和q(z|x)来最大化Lb.
图12
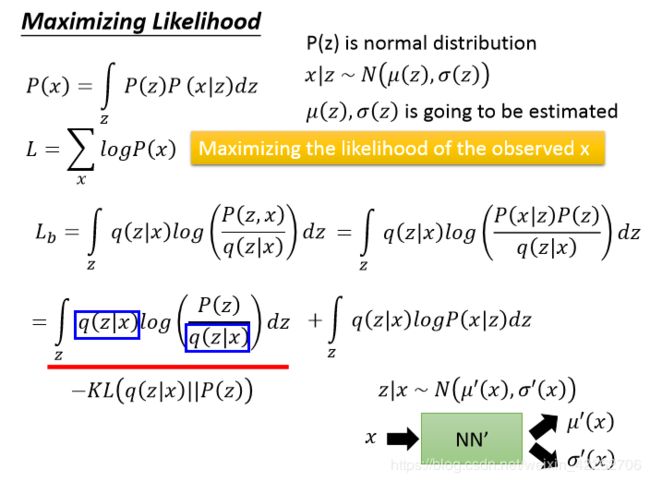
如图13： 对图12中的Lb继续化简。
图13
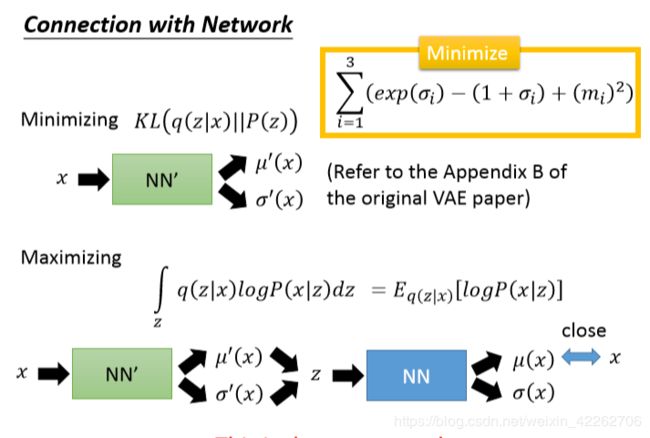
如图14，分析Lb可得，最终的目标就是最小化KL(q(z|x)||p(z))以及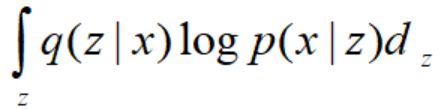最大化
，最大化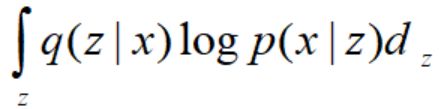
的实质就是Auto-Encoder,若再加上最小化的项，就是VAE.所以VAE与AE的差别就是控制了编码输出要服从一定的分布规律。
图14
三.VAE的缺点
VAE从来都没有去学习如何产生一张新的图片，只是保证产生一张与DATABASE中的图片尽可能相似的而已，VAE做的只是模仿，没有办法产生新的图片。因此，才产生了后来的GAN.
注：本文是对台大李宏毅教授课程的自我注解，因此其图片来源于李宏毅教授的slides.