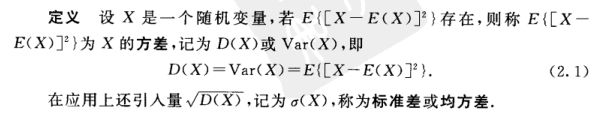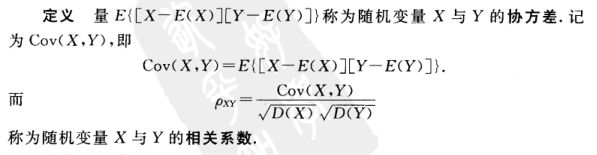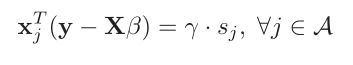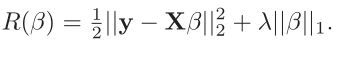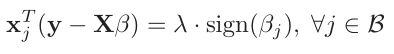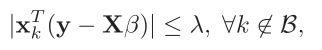机器学习--线性回归3(使用LAR算法进行求解Lasso算法)
上一节我们详细的介绍了岭回归算法和lasso算法的来历和使用,不过还没有详解lasso的计算方式,本节将进行全面的详解,在详解之前,希望大家都理解了岭回归和lasso 的来历,他们的区别以及使用的范围。下面将开始详解求解过程:
一样的,讲解之前先把本节需要的基础知识和大家讲讲,这样更容易理解:
本节需要大家理解方差、协方差以及相关系数,下面我们逐一来看一下,如果方差、协方差、相关系数的意义不理解的建议停下来好好学一学,不是只看公式,要学习公式背后的意义,这才是重点,你只有懂了深层意义,你才知道如何使用它,切记。
方差:
根据上面定义,大家知道,E(x)是均值的意思,那么X-E(x),就是衡量变量x偏离平均值的程度,但是呢X-E(x)可能为正可能为负,而且正负都可以代表偏离程度,关键是X-E(x)无法整体衡量变量x偏离中心的程度,因此就出现了![]() 的平方项,为了求整体的偏离度,因此对
的平方项,为了求整体的偏离度,因此对![]() 求均值(数据与均值相减求和在求均值)即可:
求均值(数据与均值相减求和在求均值)即可: ![]() 这就是方差了,因为前面为了防止正负抵消加了平方项,这里也要开方,开方后就是标准差了即数据平均偏离中心的程度了,因此方差是衡量数据(变量x)平均偏离中心的的程度的指标。
这就是方差了,因为前面为了防止正负抵消加了平方项,这里也要开方,开方后就是标准差了即数据平均偏离中心的程度了,因此方差是衡量数据(变量x)平均偏离中心的的程度的指标。
更深入详细的理解建议看概率论相关的书籍,上面是一维变量x 的方差的定义,那如果是二维的呢?他们的方差如何定义?这些大家自己看看。
协方差:
在这里默认大家都熟悉概率论了,我们知道在二维中,如果两个随机变量x,y相互独立,那么他么的方差![]() ,那么如果x,y不独立呢?因此协方差的定义就出来了:
,那么如果x,y不独立呢?因此协方差的定义就出来了:
协方差的理解和方差差不多,区别在于,这里的方差代表的是两个变量共同决定偏离中心的程度,上面同时也给出了相关系数,就是协方差除以标准差,为什么是需要除以各自的标准差呢?其实本质原因是消除两个变量的幅值带来的差异,因为相关系数是衡量两个变量的变化趋势的,和本身变化的多少没关系,而本身的变化多少其实就是各自的方差了,大家仔细琢磨一下就明白了。
换个角度进行解:
相关系数也可以看成协方差:一种剔除了两个变量量纲影响、标准化后的特殊协方差。
既然是一种特殊的协方差,那它:
1、也可以反映两个变量变化时是同向还是反向,如果同向变化就为正,反向变化就为负。
2、由于它是标准化后的协方差,因此更重要的特性来了:它消除了两个变量变化幅度的影响,而只是单纯反应两个变量每单位变化时的相似程度。
总结一下相关系数:衡量多个变量之间变化趋势的量,和各自的变化多少没关系,只和变化趋势相关,因此:
当他们的相关系数为1时,说明两个变量变化时的正向相似度最大,即,你变大一倍,我也变大一倍;你变小一倍,我也变小一倍。也即是完全正相关(以X、Y为横纵坐标轴,可以画出一条斜率为正数的直线,所以X、Y是线性关系的)。
随着他们相关系数减小,两个变量变化时的相似度也变小,当相关系数为0时,两个变量的变化过程没有任何相似度,也即两个变量无关。
当相关系数继续变小,小于0时,两个变量开始出现反向的相似度,随着相关系数继续变小,反向相似度会逐渐变大。
当相关系数为-1时,说明两个变量变化的反向相似度最大,即,你变大一倍,我变小一倍;你变小一倍,我变大一倍。也即是完全负相关(以X、Y为横纵坐标轴,可以画出一条斜率为负数的直线,所以X、Y也是线性关系的)。
我们知道了什么是协方差,以及协方差的定义,那么如果有一集合的样本x,y,我们去中心化,标准化后,此时的均值为0,方差为1,那么相关系数的定义就可以写成:
![]()
这是根据上面的定义写的,对E(xy)=xy这一步是因为上面进行了去中心化和标准化,后面会发现相关系数就是XY的內积,而內积的物理意义大家都知道了把,我在这篇文章详细讲解了设么是內积,这点很重要,我们发现两个变量的相关性和变量的內积有一定的关系,那么相关性越大,內积的绝对值就越大,当內积为0时说明两个变量不相关,同时说明两个向量是垂直的,如果高度相关,说明两个向量是共线的,大家需要理解,好到这里基础就讲完了,下面我们开始今天的主角LAR解决lasso:
首先需要说明的是LAR(最小角回归)和lasso是两个不同的算法,但是二者在某些方面具有惊人的相识,然而lasso 的计算相当复杂,但是LAR的计算是很简单的(这里又体现了,很复杂的数学计算一般可以通过很简单的数学计算得出,只是这个简单的数学计算没那么容易想到而已),有多简单呢?我们下面会详说,因此人们就使用LAR近似的对lasso求解,虽然说是近似,但是和真实没什么区别了,下面先从LAR进行详解:
LAR(最小角回归)
LAR(Least Angel Regression),Efron于2004年提出的一种变量选择的方法,类似于向前逐步回归(ForwardStepwise)的形式,是lasso regression的一种高效解法。向前逐步回归(Forward Stepwise)不同点在于,Forward Stepwise每次都是根据选择的变量子集,完全拟合出线性模型,计算出RSS,再设计统计量(如AIC)对较高的模型复杂度作出惩罚,而LAR是每次先找出和因变量相关度最高的那个变量, 再沿着LSE的方向一点点调整这个predictor的系数,在这个过程中,这个变量和残差的相关系数会逐渐减小,等到这个相关性没那么显著的时候,就要选进新的相关性最高的变量,然后重新沿着LSE的方向进行变动。而到最后,所有变量都被选中,就和LSE相同了。
下面我们详解一下,先讲解一下一点基础知识:
这个图大家不陌生生吧,在上一篇里我详细的讲过,不知道的请看我的这篇文章,我们知道y是真实值,而![]() 就是拟合值了,而
就是拟合值了,而![]() 的就是在x1和x2确定的平面内,找到一点是的yy^最小的回归系数,此时就是最优解了,因为此时的误差最小,那么我们联系下上面的基础可知,如果两个向量相关性为0则说明两个向量是正交的(垂直),我们还知道,距离最短时,一定是
的就是在x1和x2确定的平面内,找到一点是的yy^最小的回归系数,此时就是最优解了,因为此时的误差最小,那么我们联系下上面的基础可知,如果两个向量相关性为0则说明两个向量是正交的(垂直),我们还知道,距离最短时,一定是![]() 同时垂直x1和x2,这个不用解释了吧,那么如果推向多个变量的情况下也应该是这样既
同时垂直x1和x2,这个不用解释了吧,那么如果推向多个变量的情况下也应该是这样既![]() 应该垂直所有的
应该垂直所有的![]() 时才是最优的,这里大家一定要深入理解了,好,到这里所有基础都准备好了,下面正式引入LAR算法:
时才是最优的,这里大家一定要深入理解了,好,到这里所有基础都准备好了,下面正式引入LAR算法:
什么是最小角回归?最小角体现在哪里?:
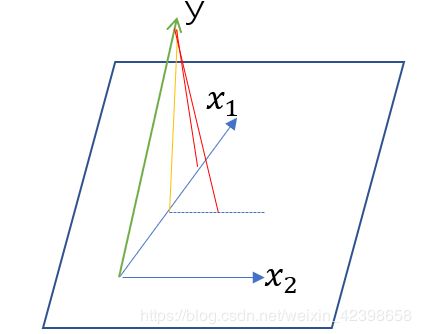
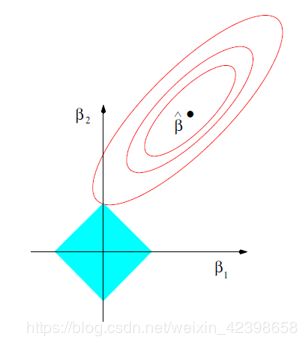
在这里首先以二维讲解,然后推向高维 ,如图,二维x1和x2张成了一张平面(看不懂的看这篇文章),那么就是在这个平面内找到最优值,其实就是找到垂直这个平面的![]() ,这个很好理解但是计算起来并不容易,现在有一种可行的方法,即我先计算所有的
,这个很好理解但是计算起来并不容易,现在有一种可行的方法,即我先计算所有的![]() 和
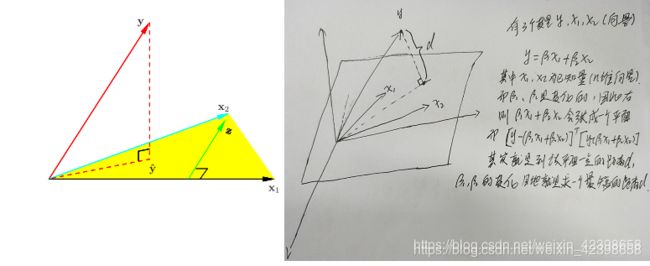
和![]() 的相关系数,然后排好序,找到相关系数最大的那个x,假如上图就是x1和y的相关性最大,那么我们要找的这一点先从x1和y交点处开始,此时先关性是最大的,那么我沿着x1的方向移动那一点,上图的黄线,此时相关性的计算相当于那个黄线的向量和x1的相关性,相关性从最大逐渐减小,在减小的过程中,在某一点,一定会和第二个向量的相关性相等,上图以x2为第二个相关性,某一点就是黄线和虚线的交点,在这一点时,yx1的相关性和yx2的相关性是相等的(虚线就是x2,和先平行),此时我做条x1和x2的角平分线,然后黄线沿着角平分线继续游走,如下图;
的相关系数,然后排好序,找到相关系数最大的那个x,假如上图就是x1和y的相关性最大,那么我们要找的这一点先从x1和y交点处开始,此时先关性是最大的,那么我沿着x1的方向移动那一点,上图的黄线,此时相关性的计算相当于那个黄线的向量和x1的相关性,相关性从最大逐渐减小,在减小的过程中,在某一点,一定会和第二个向量的相关性相等,上图以x2为第二个相关性,某一点就是黄线和虚线的交点,在这一点时,yx1的相关性和yx2的相关性是相等的(虚线就是x2,和先平行),此时我做条x1和x2的角平分线,然后黄线沿着角平分线继续游走,如下图;
此时大家知道,因为沿着角平分线走,会发现黄线和x1和x2的相关性会同样的变化,因为是內积,所以相等(平面中角平分线上的点到两边的距离相等) ,好此时我们加入的x2的相关性也一起减小了,同理减小到第三个量即x3和y的相关性相等,此时把第三个变量也加入,就这样不停的游走,直到加入所有的x,最后使相关性系数游走到零这一点,而这一点就是最优点,相关系数为零说明,內积为零,內积为零说明相互垂直,因此此时的点对所有的x都是垂直的,这也点也就是我们一直说的最优点,因此就找到了,最小角就体现在角平分线的角,因为每次改变的方向就改变![]() 角,如果是高维的情况,则说明每次改变的会更小,因此是最小角回归,这个大家需要好好理解。
角,如果是高维的情况,则说明每次改变的会更小,因此是最小角回归,这个大家需要好好理解。
好,我们总结一下最小角回归:
首先计算所有的相关性,刚开始最大的加入点就是y本身,相关性为1,然后选择最大的相关性为第一个加入点,然后游走,不停的计算相关系数,当减小到等于第二个相关系数时,把第二个变量加入,然后按照这两个角平分线继续游走,以此类推加入第三个,第四个,直到全部加入,然后游走到相关系数为0,这一点就是最优点了,以上就是最小角回归了,几何意义很清晰,能想到这样的解决方法都是牛叉之人,佩服。下面给出伪代码:
1. 对数据进行去中心化和标准化,计算残差:![]()
2.计算所有的![]() 和
和![]() 的相关系数,并选出最大的那个相关系数
的相关系数,并选出最大的那个相关系数![]()
3. 最小二乘系数![]() 从0开始移动,并时刻计算
从0开始移动,并时刻计算 ![]() (相关系数),直到和最大
(相关系数),直到和最大![]() 的相关系数相等,此时加入进来
的相关系数相等,此时加入进来
4.然后沿着![]() 共同决定的方向继续前进,直到和下一个x相关系数相等,然后加入
共同决定的方向继续前进,直到和下一个x相关系数相等,然后加入
5.按照第3,4两步。直到完全加入所有的变量x,
6.加入完以后继续游走使其相关系数为零,此时的![]() 值就是最优值。
值就是最优值。
下面我们看看图:
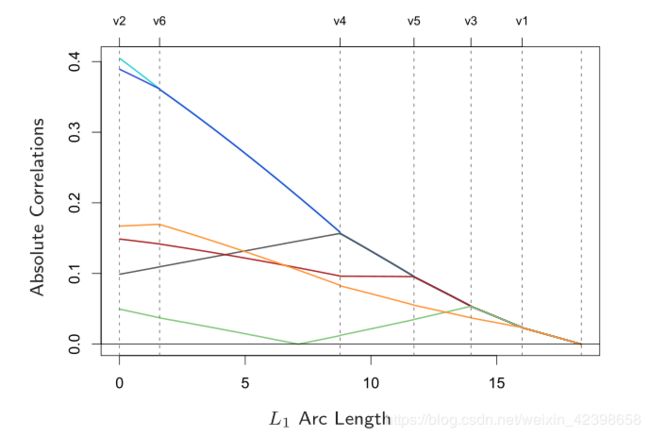
其中L1是每次加入变量后改变的弧长的累加和 详解如下:
好我们来看看上图,上图横轴为弧长,纵轴是相关系数,我们发现v2出的相关系数最大即水蓝色,即先沿着v2减小,直到在v6时和蓝线相等,然后根据角平分线继续游走减小,在v4时由加入一个,以此类推 一直加完所有的变量,然后是最后的相关系数走到0的点,此时就是最优点,从图中我们还可以发现随着不停的游走,变量的相关系数在不停的变化,这个大家应该都能理解吧,所以每游走一步都需要计算相关系数,而计算相关系数很简单就是內积就可以了,以上就是最小角回归的工作原理,下面我们看看他和lasso有什么关系:
大家看看,他们是不是很相似,只是某些细节不一样,如果我们在矫正一下是不是就是一样的呀,先给出矫正方式:
如果非零系数达到零,将其变量从活动变量集合中删除,并重新计算当前最小二乘方向。
为什么这两个算法如此相似呢?怎么回事呢?下面我们来看到底为什么他们那么像。
先说明就是那本书对这解释也是不清楚的,看的晕晕的,不过LAR容易解释,但是lasso的那个过0时产生跳跃没有讲清楚,在这里我根据我自己的理解说一下,如果哪位大神看到这里,看出眉目了,知道到底是什么原因一定要和我说呀,我也是太想知道了,好,下面开始:
LAR:
对于最小角回归我们知道,他是根据误差向量和添加的xi进行內积的,一旦內积完成在游走时,符号(正负号)一般不会变,只会改变內积的大小,因此游走表达式可以写成下式:
A就是加入游走的特征向量集了,![]() 就是就是符号函数(大于0等于1,小于零等于-1),而
就是就是符号函数(大于0等于1,小于零等于-1),而![]() 就是內积的绝对值了,他有一个条件:
就是內积的绝对值了,他有一个条件:
这个大家应该可以理解,就是没加入游走的特征的內积一定小于 ![]() ,因为內积就是相关系数啊,游走的顺序是先从大的相关系数开始,逐渐减小到0的,因此还没加入的特征肯定小于
,因为內积就是相关系数啊,游走的顺序是先从大的相关系数开始,逐渐减小到0的,因此还没加入的特征肯定小于![]() 的,这个大家可以理解对吧,那么加入符号函数的目的是因为特征向量可能是相反的即相关系数可能为负的,这个也容易理解,根据这个图来看,没有什么特殊的点不满足条件,因此是连续的,那么我看看lasso :
的,这个大家可以理解对吧,那么加入符号函数的目的是因为特征向量可能是相反的即相关系数可能为负的,这个也容易理解,根据这个图来看,没有什么特殊的点不满足条件,因此是连续的,那么我看看lasso :
这个是我们最初优化的那个式子即误差平方和,只是假如了一阶的惩罚函数也就是lasso了 。通过这个式子我们需要解出![]() ,那就需要求导,因为加了绝对值,因此需要分情况讨论,需要找到满足所有驻点的关系式,于是经过大量的数学推倒找到了这个满足所有驻点的方程式:
,那就需要求导,因为加了绝对值,因此需要分情况讨论,需要找到满足所有驻点的关系式,于是经过大量的数学推倒找到了这个满足所有驻点的方程式:
我们发现和lar很像,不同的是符号函数的情况,这也是导致差异的原因 ,我们知道得到这个式子的前提是对上式的求导,但是大家想想,这里都满足可导吗?请看下图:
我们发现除了约束条件的四个顶点不可导以外,其他均可导,不可导的情况就是某一个 ![]() 为0,这也是是解释了为什么产生跳跃的原因,当然这是我的理解,仔细想想还是有点不对,但是那本书讲的更简略,他说是因为不满足下面这个条件:
为0,这也是是解释了为什么产生跳跃的原因,当然这是我的理解,仔细想想还是有点不对,但是那本书讲的更简略,他说是因为不满足下面这个条件:
为了大神能看到,我把原文贴上来:
其中3.23时就是我们最初的回归表达式:
有搞明白的请留言,谢谢,或者加我微信zsffuture。
本篇就到此结束,基本上线性回归的理论就结束了,后面就是根据机器学习实战进行实现了,后面的就不难了,如果理解到这里你的思路还是很清晰说明你已经彻底的理解了,好,本节结束
注:原书为:The Elements of Statistical Learning ,这本书很好,但是本节说的不清楚,可能是我的知识面受限吧。