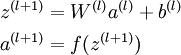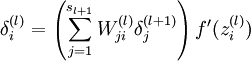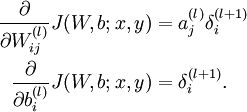深度学习基础面试问题汇总

第一部分：深度学习

1、神经网络基础问题

（1）Backpropagation（要能推倒）

后向传播是在求解损失函数L对参数w求导时候用到的方法，目的是通过链式法则对参数进行一层一层的求导。这里重点强调：要将参数进行随机初始化而不是全部置0，否则所有隐层的数值都会与输入相关，这称为对称失效。
大致过程是:

首先前向传导计算出所有节点的激活值和输出值，

计算整体损失函数：

然后针对第L层的每个节点计算出残差（这里是因为UFLDL中说的是残差，本质就是整体损失函数对每一层激活值Z的导数），所以要对W求导只要再乘上激活函数对W的导数即可

（2）梯度消失、梯度爆炸

梯度消失：这本质上是由于激活函数的选择导致的， 最简单的sigmoid函数为例，在函数的两端梯度求导结果非常小（饱和区），导致后向传播过程中由于多次用到激活函数的导数值使得整体的乘积梯度结果变得越来越小，也就出现了梯度消失的现象。
　　梯度爆炸：同理，出现在激活函数处在激活区，而且权重W过大的情况下。但是梯度爆炸不如梯度消失出现的机会多。

（3）常用的激活函数

softmax交叉熵损失函数导数的推导

一般情况下，在神经网络中，最后一个输出层的节点个数与分类任务的目标数相等。假设最后的节点数为N，那么对于每一个样例，神经网络可以得到一个N维的数组作为输出结果，数组中每一个维度会对应一个类别。在最理想的情况下，如果一个样本属于k，那么这个类别所对应的的输出节点的输出值应该为1，而其他节点的输出都为0，即[0,0,1,0,….0,0]，这个数组也就是样本的Label，是神经网络最期望的输出结果，交叉熵就是用来判定实际的输出与期望的输出的接近程度！
交叉熵刻画的是实际输出（概率）与期望输出（概率）的距离，也就是交叉熵的值越小，两个概率分布就越接近。假设概率分布p为期望输出，概率分布q为实际输出，H(p,q)为交叉熵，则：
$$H(p,q)=-\sum _{x}p(x)logq(x)$$
除此之外，交叉熵还有另一种表达形式，还是使用上面的假设条件：

$$H(p,q)=-\sum _x(p(x)logq(x)+(1-p(x))log(1-q(x)))$$
softmax用于多分类过程中，它将多个神经元的输出，映射到（0,1）区间内，可以看成概率来理解。softmax就是将原来输出通过softmax函数一作用，就映射成为(0,1)的值，而这些值的累和为1（满足概率的性质），那么我们就可以将它理解成概率，在最后选取输出结点的时候，我们就可以选取概率最大（也就是值对应最大的）结点，作为我们的预测目标。
假设我们有一个数组V，$V_i$表示V中的第i个元素，那么这个元素的softmax值就是：

$$S_i=\frac{e^{V_i}}{{\sum }_k{e}^{V_k}}$$

softmax交叉熵损失函数
$$C=-\sum _i{y}_{i}ln{a}_i$$
其中，$y_i$表示真实的分类结果，$a_i$表示softmax第i个输出值。
我们要求的是loss对于神经元输出（$z_i$）的梯度，即：
$$\frac{\partial C}{\partial z_i}$$
根据复合函数求导法则，可得：

$$\frac{\partial C}{\partial z_i}=\frac{\partial C}{\partial a_j}\frac{\partial a_j}{\partial z_i}$$
其中：

$$\frac{\partial C}{\partial a_j}=-\sum _j{y}_j\frac{1}{a_j}$$
针对$\frac{\partial a_j}{\partial z_i}$，将其分为两种情况，
当i=j:
$$\frac{\partial a_i}{\partial z_i}=\frac{\partial \frac{e^{z_i}}{{\sum }_k{e}^{z_k}}}{\partial z_i}=\frac{e^{z_i}{\sum }_k{e}^{z_k}-(e^{z_i}{)}^2}{({\sum }_k{e}^{z_k}{)}^2}=\frac{e^{z_i}}{{\sum }_k{e}^{z_k}}(1-\frac{e^{z_i}}{{\sum }_k{e}^{z_k}})=a_i(1-a_i)$$
当i≠j：
$$\frac{\partial a_j}{\partial z_i}=\frac{\partial \frac{e^{z_j}}{{\sum }_k{e}^{z_k}}}{\partial z_i}=-e^{z_j}(\frac{1}{{\sum }_k{e}^{z_k}}{)}^2{e}^{z_i}=-a_i{a}_j$$
故，
$$\begin{gathered} \frac{\partial C}{\partial z_i}=-\sum _j{y}_j\frac{1}{a_j}(\frac{\partial a_j}{\partial z_i})=-\frac{y_i}{a_i}(a_i(1-a_i))+\sum _{j\ne i}\frac{y_j}{a_j}{a}_i{a}_j=-y_i+y_i{a}_i+\sum _{j\ne i}{y}_j{a}_i \\ =-y_i+a_i\sum _j{y}_j=a_i-y_i \end{gathered}$$

以上的所有说明针对的都是单个样例的情况，而在实际的使用训练过程中，数据往往是组合成为一个batch来使用，所以对用的神经网络的输出应该是一个m*n的二维矩阵，其中m为batch的个数，n为分类数目，而对应的Label也是一个二维矩阵，还是拿上面的数据，组合成一个batch=2的矩阵：

在TensorFlow中实现交叉熵
在TensorFlow可以采用这种形式：

cross_entropy = -tf.reduce_mean(y_ * tf.log(tf.clip_by_value(y, 1e-10, 1.0))) 

其中y_表示期望的输出，y表示实际的输出（概率值），*为矩阵元素间相乘，而不是矩阵乘。
上述代码实现了第一种形式的交叉熵计算，需要说明的是，计算的过程其实和上面提到的公式有些区别，按照上面的步骤，平均交叉熵应该是先计算batch中每一个样本的交叉熵后取平均计算得到的，而利用tf.reduce_mean函数其实计算的是整个矩阵的平均值，这样做的结果会有差异，但是并不改变实际意义。
除了tf.reduce_mean函数，tf.clip_by_value函数是为了限制输出的大小，为了避免log0为负无穷的情况，将输出的值限定在(1e-10, 1.0)之间，其实1.0的限制是没有意义的，因为概率怎么会超过1呢。

由于在神经网络中，交叉熵常常与Sorfmax函数组合使用，所以TensorFlow对其进行了封装，即：

cross_entropy = tf.nn.sorfmax_cross_entropy_with_logits(y_ ,y) 

与第一个代码的区别在于，这里的y用神经网络最后一层的原始输出就好了。

（4）参数更新方法

方法名称	公式	算法介绍
Vanilla update	$$x=x-learnin{g}_{rate}\ast dx$$	当训练数据太多时，利用整个数据集更新往往时间上不显示。batch的方法可以减少机器的压力，并且可以更快地收敛当训练集有很多冗余时（类似的样本出现多次），batch方法收敛更快。以一个极端情况为例，若训练集前一半和后一半梯度相同。那么如果前一半作为一个batch，后一半作为另一个batch，那么在一次遍历训练集时，batch的方法向最优解前进两个step，而整体的方法只前进一个step
Momentum update动量更新	$$v=mu\ast v-learnin{g}_{rate}\ast dx$$ # integrate velocity$$x=x+v$$ # integrate position	momentum即动量，它模拟的是物体运动时的惯性，即更新的时候在一定程度上保留之前更新的方向，同时利用当前batch的梯度微调最终的更新方向。这样一来，可以在一定程度上增加稳定性，从而学习地更快，并且还有一定摆脱局部最优的能力：
Nesterov Momentum	$$x_{ahead}=x+mu\ast v$$ $$v=mu\ast v-learnin{g}_{rate}\ast {dx}_{ahead}$$ x += v
Adagrad (自适应的方法，梯度大的方向学习率越来越小,由快到慢)	$$cache+=dx\ast \ast 2$$$$x+=-learnin{g}_{rate}\ast dx/(np.sqrt(cache)+eps)$$
Adam	$$m=beta1\ast m+(1-beta1)dx$$ $$v=beta2\ast v+(1-beta2)(dx\ast \ast 2)$$ $$x=x-learnin{g}_{rate}\ast m/(np.sqrt(v)+eps)$$

（5）解决overfitting的方法

dropout， regularization， batch normalizatin，但是要注意dropout只在训练的时候用，让一部分神经元随机失活。
　　Batch normalization是为了让输出都是单位高斯激活，方法是在连接和激活函数之间加入BatchNorm层，计算每个特征的均值和方差进行规则化。

（6）常用的损失函数

经典机器学习算法，他们最本质的区别是分类思想（预测y的表达式）不同，有的是基于概率模型，有的是动态规划，表象的区别就是最后的损失函数不同。

损失函数分为经验风险损失函数和结构风险损失函数，经验风险损失函数反映的是预测结果和实际结果之间的差别，结构风险损失函数则是经验风险损失函数加上正则项(L0、L1（Lasso）、L2（Ridge）)。

不同的算法常用的损失函数（Loss Function）有：

一、0-1损失函数（gold standard 标准式）

   0-1损失是指，预测值和目标值不相等为1，否则为0： 

                                               

  该损失函数不考虑预测值和真实值的误差程度，也就是说只要预测错误，预测错误差一点和差很多是一样的。感知机就是用的这种损失函数，但是由于相等这个条件太过严格，我们可以放宽条件，即满足 |Y−f(X)|

二、绝对值损失函数

    绝对值损失函数，（暂时还不知道用在啥场合，了解后改正）：

三、平方损失函数（squared loss）

   实际结果和观测结果之间差距的平方和，一般用在线性回归中，可以理解为最小二乘法：

四、对数损失函数（logarithmic loss）

   主要在逻辑回归中使用，样本预测值和实际值的误差符合高斯分布，使用极大似然估计的方法，取对数得到损失函数：

                                                         

   损失函数L(Y,P(Y|X))L(Y,P(Y|X))是指样本X在分类Y的情况下，使概率P(Y|X)达到最大值。

   经典的对数损失函数包括entropy和softmax，一般在做分类问题的时候使用（而回归时多用绝对值损失（拉普拉斯分布时，μ值为中位数）和平方损失（高斯分布时，μ值为均值））。

五、指数损失函数（Exp-Loss）

   在boosting算法中比较常见，比如Adaboosting中，标准形式是：

六、铰链损失函数（Hinge Loss）

   铰链损失函数主要用在SVM中，Hinge Loss的标准形式为：

                                                          

   y是预测值，在-1到+1之间，t为目标值（-1或+1）。其含义为，y的值在-1和+1之间就可以了，并不鼓励|y|>1|y|>1，即并不鼓励分类器过度自信，让某个正确分类的样本的距离分割线超过1并不会有任何奖励，从而使分类器可以更专注于整体的分类误差。