2020-6-13 吴恩达-NN&DL-w3 浅层NN(课后编程-Planar data classification with one hidden layer)

原文链接
如果打不开，也可以复制链接到https://nbviewer.jupyter.org中打开。

本次练习将构建一个单隐层NN。你会发现这个模型和ML的逻辑回归模型有很大的区别。

单隐层NN是非线性的。而ML的逻辑回归模型是线性的。

你将会学习

• 构建一个单隐层2分分类NN
• 使用具有非线性激活函数神经元，例如tanh函数
• 计算交叉熵损失（损失函数）
• 实现前向传播和反向传播

1.本文涉及的基本库

本作业涉及以下几个python库

• numpy ：是用Python进行科学计算的基本软件包。
• sklean ：是数据挖掘和数据分析简单有效的工具。
• matplotlib：是一个著名的库，用于在Python中绘制图表。
• testCases.py：提供了一些测试样本来评估你的函数的正确性。
• planar_utils.py：提供了在本作业中会使用的各种有用的函数。

import numpy as np
import matplotlib.pyplot as plt
from testCases import *
import sklearn
import sklearn.datasets
import sklearn.linear_model
from planar_utils import plot_decision_boundary, sigmoid, load_planar_dataset, load_extra_datasets

#%matplotlib inline #如果你使用用的是Jupyter Notebook的话请取消注释。

np.random.seed(1) # set a seed so that the results are consistent设置一个固定的随机种子，以保证接下来的步骤中结果是一致的。

2.数据集 Dataset

首先，让我们获取将要使用的数据集， 下面的代码会将一个包含“花的图形”的2分分类数据集加载到变量X和Y中。

X, Y = load_planar_dataset()

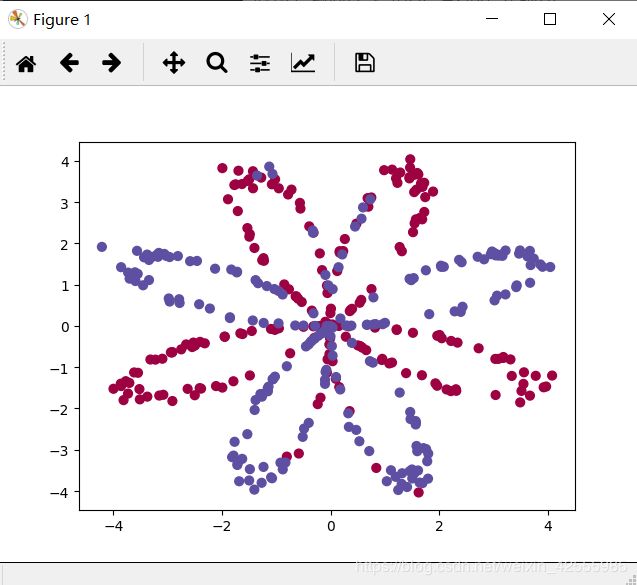
使用 matplotlib可视化数据集。看上去就象一朵花，它由一些红色点（标签y=0）和蓝色点（标签y=1）组成。
你的目标就是要构建一个模型拟合(fit)这些数据。

# Visualize the data: 可视化数据
plt.scatter(X[0, :], X[1, :], c=Y, s=40, cmap=plt.cm.Spectral);#绘制散点图
plt.show()

运行结果如下图

补充，load_planar_dataset函数内容如下

def load_planar_dataset():
    np.random.seed(1)
    m = 400 # number of examples
    N = int(m/2) # number of points per class
    D = 2 # dimensionality
    X = np.zeros((m,D)) # data matrix where each row is a single example
    Y = np.zeros((m,1), dtype='uint8') # labels vector (0 for red, 1 for blue)
    a = 4 # maximum ray of the flower

    for j in range(2):
        ix = range(N*j,N*(j+1))
        t = np.linspace(j*3.12,(j+1)*3.12,N) + np.random.randn(N)*0.2 # theta
        r = a*np.sin(4*t) + np.random.randn(N)*0.2 # radius
        X[ix] = np.c_[r*np.sin(t), r*np.cos(t)]
        Y[ix] = j
        
    X = X.T
    Y = Y.T

    return X, Y

现在你已经有了

• 一个numpy矩阵X，包含特征$x_1$和$x_2$
• 一个numpy矩阵Y，包含分类标签(红色:0, 蓝色:1)

让我们更好地了解我们的数据是什么样的。例如

• 有多少训练样本
• 变量X和Y的形状是怎么样的

代码如下

### START CODE HERE ### (≈ 3 lines of code)
shape_X = X.shape
shape_Y = Y.shape
m = Y.shape[1]  # training set size
### END CODE HERE ###

print ('The shape of X is: ' + str(shape_X))
print ('The shape of Y is: ' + str(shape_Y))
print ('I have m = %d training examples!' % (m))

运行结果如下

The shape of X is: (2, 400)
The shape of Y is: (1, 400)
I have m = 400 training examples!

3.简单逻辑回归分类器(线性分类)–效果不佳

在构建完整的NN之前，让我们先看看逻辑回归在这个问题上的表现如何。你可以使用sklearn的内置函数来实现。

在数据集上训练逻辑回归分类器，代码如下。

clf = sklearn.linear_model.LogisticRegressionCV()
clf.fit(X.T,Y.T)

运行后显示结果如下

C:\Users\toddc\Anaconda3\lib\site-packages\sklearn\utils\validation.py:526: DataConversionWarning: A column-vector y was passed when a 1d array was expected. Please change the shape of y to (n_samples, ), for example using ravel().
  y = column_or_1d(y, warn=True)

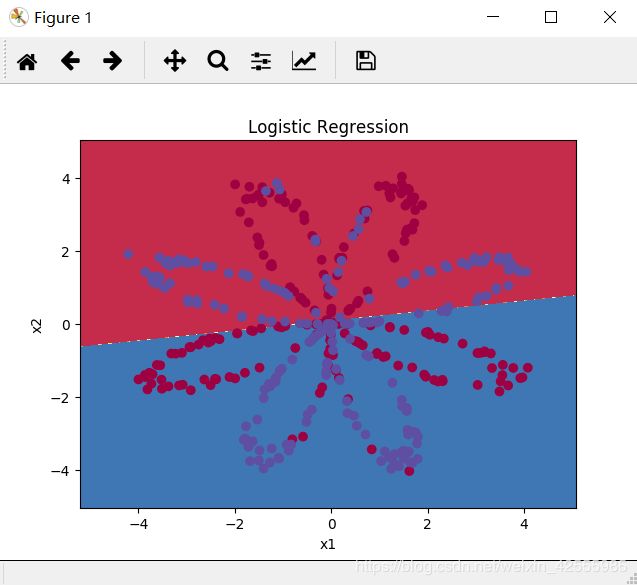
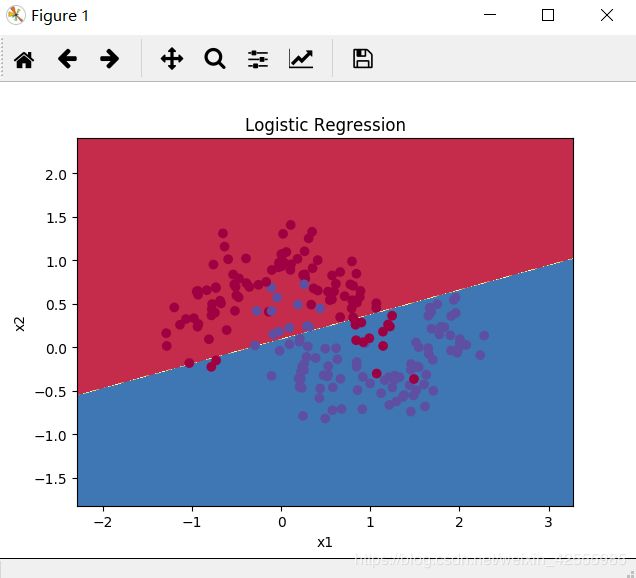
你可以绘制模型的决策边界。代码如下

# Plot the decision boundary for logistic regression 绘制逻辑回归决策边界
plot_decision_boundary(lambda x: clf.predict(x), X, Y)
plt.title("Logistic Regression")
plt.show()

# Print accuracy
LR_predictions = clf.predict(X.T) #预测
#print ('Accuracy of logistic regression: %d ' % float((np.dot(Y, LR_predictions) + np.dot(1 - Y,1 - LR_predictions)) / float(Y.size) * 100) +
#       '% ' + "(percentage of correctly labelled datapoints)")
print ("逻辑回归的准确率： %d " % float((np.dot(Y, LR_predictions) + 
		np.dot(1 - Y,1 - LR_predictions)) / float(Y.size) * 100) +
       "% " + "(正确标签的数据点所占的百分比)")

运行结果如下

逻辑回归的准确率： 47 % (正确标签的数据点所占的百分比)

分类结果如下

准确率只有47%的原因是该数据集显然不是线性可分的，所以逻辑回归分类器表现不佳。
希望NN可以表现的更好。

4.单隐层NN模型

逻辑回归在“花”数据集上表现不佳。现在我们来训练单隐层NN。

下图是我们的模型

模型的数学公式，可以参见链接

对于训练样本$x^{(i)}$:
$z^{[1](i)}=W^{1]}{x}^{(i)}+b^{[1](i)}$
$a^{[1](i)}=tanh(z^{[1](i)})$
$z^{[2](i)}=W^{[2]}{a}^{[1](i)}+b^{[2](i)}$
预测值为$${\hat{y}}^{(i)}=a^{[2](i)}=\sigma (z^{[2](i)})=\{\begin{array}{ll}1,& \text{if a[2](i)>0.5}\\ 0,& \text{otherwise}\end{array}$$
获得所有样本的预测值之后，你可以计算成本
$$J=-\frac{1}{m}\sum _{i=0}^m(y^{(i)}log(a^{[2](i)})+(1-y^{(i)})log(1-a^{[2](i)}))$$

建立NN的一般办法如下

• 定义NN结构（输入单元，隐藏单元等等）
• 初始化模型的参数
• 循环
  • 实现前向传播
  • 计算损失
  • 实现反向传播，获得梯度
  • 更新参数（梯度下降）

通常将上述1-3步分别定义成一个辅助函数，再把它们合并到一个函数中nn_model()。在构筑好nn_model()，并迭代获取到正确的参数之后，即可对新数据进行预测。

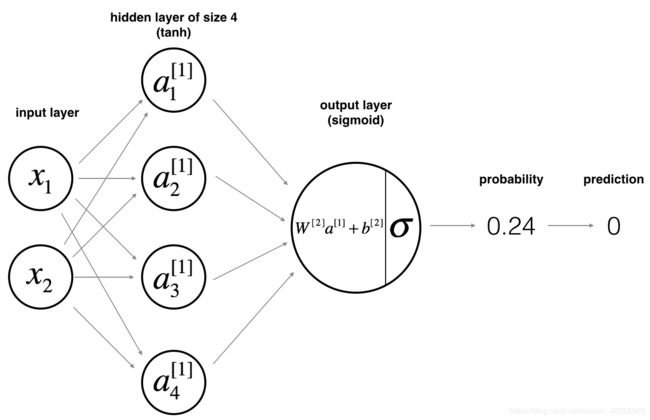
4.1定义NN结构

定义3个变量

• n_x: 输入层（单元）的数量
• n_h: 隐藏层（单元）的数量-在这里设置为4
• n_y: 输出层（单元）的数量

使用矩阵X和Y的大小定义n_x和n_y。同时n_h赋值为4。代码如下

# GRADED FUNCTION: layer_sizes

def layer_sizes(X, Y):
    """
    Arguments:
    X -- input dataset of shape (input size, number of examples) 输入数据集,维度为（输入的数量，样本的数量）
    Y -- labels of shape (output size, number of examples) 标签，维度为（输出的数量，样本的数量）
    
    Returns:
    n_x -- the size of the input layer
    n_h -- the size of the hidden layer
    n_y -- the size of the output layer
    """
    ### START CODE HERE ### (≈ 3 lines of code)
    n_x = X.shape[0] # size of input layer
    n_h = 4
    n_y = Y.shape[0] # size of output layer
    ### END CODE HERE ###
    return (n_x, n_h, n_y)

利用testCases.py的测试函数layer_sizes_test_case()，可以试一下效果

X_assess, Y_assess = layer_sizes_test_case()
(n_x, n_h, n_y) = layer_sizes(X_assess, Y_assess)
print("The size of the input layer is: n_x = " + str(n_x))
print("The size of the hidden layer is: n_h = " + str(n_h))
print("The size of the output layer is: n_y = " + str(n_y))

运行结果如下

The size of the input layer is: n_x = 5
The size of the hidden layer is: n_h = 4
The size of the output layer is: n_y = 2

注意：这不是我们“花”的数据集的结构。只是测试案例模拟的结构。

4.2初始化模型参数

初始化模型参数是通过实现initialize_parameters()函数来完成。

说明：

• 请根据上面NN的模型图，确保你参数的大小是正确的。
• 用随机值初始化你的权重矩阵。利用np.random.randn(a,b) * 0.01来随机初始化一个维度为(a，b)的矩阵。
• 偏移向量初始化为零。利用np.zeros((a,b))来给一个维度为(a，b)的矩阵赋值零。

初始化代码如下

# GRADED FUNCTION: initialize_parameters

def initialize_parameters(n_x, n_h, n_y):
    """
    Argument:
    n_x -- size of the input layer
    n_h -- size of the hidden layer
    n_y -- size of the output layer
    
    Returns:
    params -- python dictionary containing your parameters:
                    W1 -- weight matrix of shape (n_h, n_x)
                    b1 -- bias vector of shape (n_h, 1)
                    W2 -- weight matrix of shape (n_y, n_h)
                    b2 -- bias vector of shape (n_y, 1)
    """
    
    #设置了一个种子，尽管初始化是随机的，依然可以确保输出与我们的匹配。
    np.random.seed(2) # we set up a seed so that your output matches ours although the initialization is random.
    
    ### START CODE HERE ### (≈ 4 lines of code)
    W1 = np.random.randn(n_h, n_x) * 0.01
    b1 = np.zeros(shape=(n_h, 1))
    W2 = np.random.randn(n_y, n_h) * 0.01
    b2 = np.zeros(shape=(n_y, 1))
    ### END CODE HERE ###
    
    #使用断言确保数据格式是正确的
    assert (W1.shape == (n_h, n_x))
    assert (b1.shape == (n_h, 1))
    assert (W2.shape == (n_y, n_h))
    assert (b2.shape == (n_y, 1))
    
    parameters = {"W1": W1,
                  "b1": b1,
                  "W2": W2,
                  "b2": b2}
    
    return parameters

利用testCases.py的测试函数initialize_parameters_test_case()试一下效果

n_x, n_h, n_y = initialize_parameters_test_case()

parameters = initialize_parameters(n_x, n_h, n_y)
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))

运行后，得到结果如下

W1 = [[-0.00416758 -0.00056267]
 [-0.02136196  0.01640271]
 [-0.01793436 -0.00841747]
 [ 0.00502881 -0.01245288]]
b1 = [[ 0.]
 [ 0.]
 [ 0.]
 [ 0.]]
W2 = [[-0.01057952 -0.00909008  0.00551454  0.02292208]]
b2 = [[ 0.]]

initialize_parameters_test_case()定义如下

def initialize_parameters_test_case():
    n_x, n_h, n_y = 2, 4, 1
    return n_x, n_h, n_y

就是给n_x, n_h, n_y赋值，在这里似乎可以直接使用实际数据，完全没有必要搞个测试函数。
当然，如果你数据量很大的情况，可以用上述的方法，使用测试函数，而不必导入实际数据集来获得结构数据n_x, n_h, n_y，节省初始化参数函数initialize_parameters()的测试时间。

4.3循环

4.3.1实现前向传播

说明：

• 请参照上面分类器模型的数学公式
• 使用sigmoid()函数，它包含在planar_utils.py中。
• 使用np.tanh()函数，它是numpy的内置函数。
• 实现步骤如下
  • 使用parameters[".."]从字典“parameters”中获取参数。它是由initialize_parameters()函数输出的。
  • 实现向前传播, 计算$Z^{[1]}$,$A^{[1]}$,$Z^{[2]}$,$A^{[2]}$（ 训练集里面所有样本的预测向量）。
  • 反向传播需要的值都保存在”cache“中。cache将作为反向传播函数的输入。

4.3.1.1 构建forward_propagation()函数。

代码如下

# GRADED FUNCTION: forward_propagation

def forward_propagation(X, parameters):
    """
    Argument:
    X -- input data of size (n_x, m)
    parameters -- python dictionary containing your parameters (output of initialization function)
    
    Returns:
    A2 -- The sigmoid output of the second activation
    cache -- a dictionary containing "Z1", "A1", "Z2" and "A2"
    """
    # Retrieve each parameter from the dictionary "parameters"
    ### START CODE HERE ### (≈ 4 lines of code)
    W1 = parameters['W1']
    b1 = parameters['b1']
    W2 = parameters['W2']
    b2 = parameters['b2']
    ### END CODE HERE ###
    
    # Implement Forward Propagation to calculate A2 (probabilities)
    # 实现前向传播计算A2（预测值）
    ### START CODE HERE ### (≈ 4 lines of code)
    Z1 = np.dot(W1, X) + b1
    A1 = np.tanh(Z1)
    Z2 = np.dot(W2, A1) + b2
    A2 = sigmoid(Z2)
    ### END CODE HERE ###
    
    #使用断言确保我的数据格式是正确的
    assert(A2.shape == (1, X.shape[1]))
    
    cache = {"Z1": Z1,
             "A1": A1,
             "Z2": Z2,
             "A2": A2}
    
    return A2, cache

测试一下

X_assess, parameters = forward_propagation_test_case()

A2, cache = forward_propagation(X_assess, parameters)

# Note: we use the mean here just to make sure that your output matches ours. 
print("forward_propagation：",np.mean(cache['Z1']), np.mean(cache['A1']), np.mean(cache['Z2']), np.mean(cache['A2']))

运行结果如下

forward_propagation： -0.000499755777742 -0.000496963353232 0.000438187450959 0.500109546852

现在我们已经计算了$A^{[2]}$(或者说$\hat{y}$)，其中$a^{[2](i)}$包含了训练集里每个样本预测值，下面就可以构建成本函数了。

4.3.1.2 构建compute_cost()函数

实现compute_cost()函数，计算整个数据集的成本值
$$J=-\frac{1}{m}\sum _{i=0}^m(y^{(i)}log(a^{[2](i)})+(1-y^{(i)})log(1-a^{[2](i)}))$$

说明：

• 有很多方法可以计算交叉熵损失。在python中计算交叉熵损失函数$-{\sum }_{i=0}^m{y}^{(i)}log(a^{[2](i)})$可以用如下的两步骤实现:

logprobs = np.multiply(np.log(A2),Y) #对应元素相乘
cost = - np.sum(logprobs)            # 不需要使用循环就可以直接算出来。

当然，你也可以使用np.multiply（）然后使用np.sum（）或者直接使用np.dot（）。

成本计算实现如下

# GRADED FUNCTION: compute_cost

def compute_cost(A2, Y, parameters):
    """
    Computes the cross-entropy cost given in equation (13)
    
    Arguments:
    A2 -- The sigmoid output of the second activation, of shape (1, number of examples)
    Y -- "true" labels vector of shape (1, number of examples)
    parameters -- python dictionary containing your parameters W1, b1, W2 and b2
    
    Returns:
    cost -- cross-entropy cost given equation (13)
    """
    
    m = Y.shape[1] # number of example
    
    # Retrieve W1 and W2 from parameters
    ### START CODE HERE ### (≈ 2 lines of code)
    W1 = parameters['W1']
    W2 = parameters['W2']
    ### END CODE HERE ###
    
    # Compute the cross-entropy cost#计算成本
    ### START CODE HERE ### (≈ 2 lines of code)
    logprobs = np.multiply(np.log(A2), Y) + np.multiply((1 - Y), np.log(1 - A2))
    cost = - np.sum(logprobs) / m
    ### END CODE HERE ###
    
    cost = np.squeeze(cost)     # makes sure cost is the dimension we expect. 
                                # E.g., turns [[17]] into 17 
    assert(isinstance(cost, float))
    
    return cost

测试一下

A2, Y_assess, parameters = compute_cost_test_case()

print("cost = " + str(compute_cost(A2, Y_assess, parameters)))

运行结果如下

cost = 0.692919893776

4.3.2实现反向传播

使用前向传播计算得到的cache，我们可以来实现反向传播backward_propagation()。

说明：反向传播通常是DL中最难（数学意义上）部分。为了帮助你，我们把讲义中的内容再次归纳如下。为了构建向量化的实现，你需要6个方程式。

提示：

• 为了计算dZ1，你需要计算 $g^{[1]\prime }(Z^{[1]})$， $g^{[1]}()$是tanh激活函数。如果$a=g^{[1]}(z)$，那么$g^{[1]\prime }(Z)=1-a^2$。所以我们需要使用 (1 - np.power(A1, 2))来计算 $g^{[1]\prime }(Z^{[1]})$ 。

4.3.2.1 构建backward_propagation()函数

代码如下

# GRADED FUNCTION: backward_propagation

def backward_propagation(parameters, cache, X, Y):
    """
    Implement the backward propagation using the instructions above.
    
    Arguments:
    parameters -- python dictionary containing our parameters 
    cache -- a dictionary containing "Z1", "A1", "Z2" and "A2".
    X -- input data of shape (2, number of examples)
    Y -- "true" labels vector of shape (1, number of examples)
    
    Returns:
    grads -- python dictionary containing your gradients with respect to different parameters
                  包含W和b的导数（梯度）一个字典类型的变量
    """
    m = X.shape[1]
    
    # First, retrieve W1 and W2 from the dictionary "parameters".
    ### START CODE HERE ### (≈ 2 lines of code)
    W1 = parameters['W1']
    W2 = parameters['W2']
    ### END CODE HERE ###
        
    # Retrieve also A1 and A2 from dictionary "cache".
    ### START CODE HERE ### (≈ 2 lines of code)
    A1 = cache['A1']
    A2 = cache['A2']
    ### END CODE HERE ###
    
    # Backward propagation: calculate dW1, db1, dW2, db2. 
    ### START CODE HERE ### (≈ 6 lines of code, corresponding to 6 equations on slide above)
    dZ2= A2 - Y
    dW2 = (1 / m) * np.dot(dZ2, A1.T)
    db2 = (1 / m) * np.sum(dZ2, axis=1, keepdims=True)
    dZ1 = np.multiply(np.dot(W2.T, dZ2), 1 - np.power(A1, 2))
    dW1 = (1 / m) * np.dot(dZ1, X.T)
    db1 = (1 / m) * np.sum(dZ1, axis=1, keepdims=True)
    ### END CODE HERE ###
    
    grads = {"dW1": dW1,
             "db1": db1,
             "dW2": dW2,
             "db2": db2}
    
    return grads

测试一下

parameters, cache, X_assess, Y_assess = backward_propagation_test_case()

grads = backward_propagation(parameters, cache, X_assess, Y_assess)
print ("dW1 = "+ str(grads["dW1"]))
print ("db1 = "+ str(grads["db1"]))
print ("dW2 = "+ str(grads["dW2"]))
print ("db2 = "+ str(grads["db2"]))

运行结果如下

dW1 = [[ 0.01018708 -0.00708701]
 [ 0.00873447 -0.0060768 ]
 [-0.00530847  0.00369379]
 [-0.02206365  0.01535126]]
db1 = [[-0.00069728]
 [-0.00060606]
 [ 0.000364  ]
 [ 0.00151207]]
dW2 = [[ 0.00363613  0.03153604  0.01162914 -0.01318316]]
db2 = [[ 0.06589489]]

4.3.2.2 更新参数

使用梯度下降。你可以使用(dW1, db1, dW2, db2)来更新(W1, b1, W2, b2)。

梯度下降规则：$\theta =\theta -\alpha \frac{\partial J}{\partial \theta }$

• $\alpha$：学习率
• $\theta$：待更新的参数

选择好的学习率，迭代才会收敛（converging），如下图

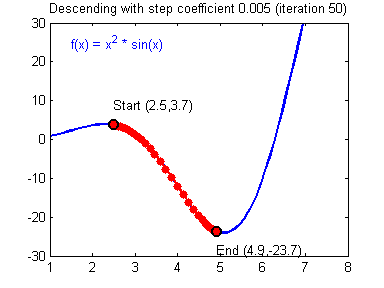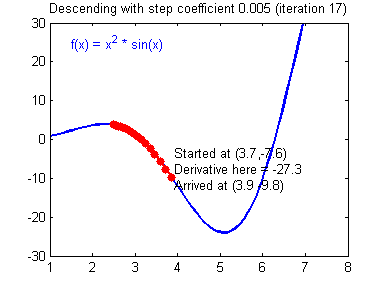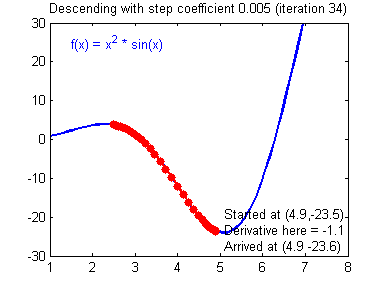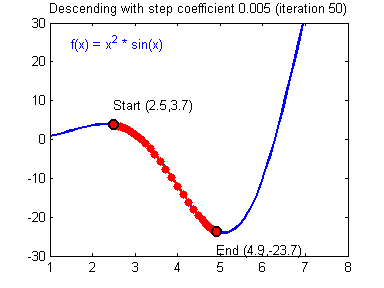
否则迭代过程不断振荡，呈发散状态（diverging），如下图

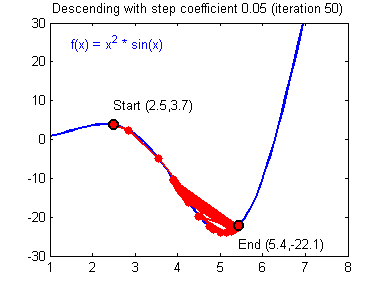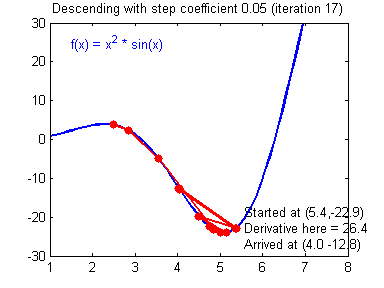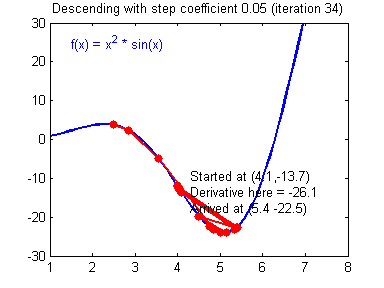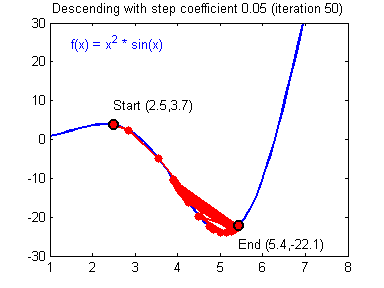
实现代码如下

# GRADED FUNCTION: update_parameters

def update_parameters(parameters, grads, learning_rate=1.2):
    """
    Updates parameters using the gradient descent update rule given above
    
    Arguments:
    parameters -- python dictionary containing your parameters 
    grads -- python dictionary containing your gradients 
    
    Returns:
    parameters -- python dictionary containing your updated parameters 
                           包含更新参数的python 字典类型的变量
    """
    # Retrieve each parameter from the dictionary "parameters"
    ### START CODE HERE ### (≈ 4 lines of code)
    W1 = parameters['W1']
    b1 = parameters['b1']
    W2 = parameters['W2']
    b2 = parameters['b2']
    ### END CODE HERE ###
    
    # Retrieve each gradient from the dictionary "grads"
    ### START CODE HERE ### (≈ 4 lines of code)
    dW1 = grads['dW1']
    db1 = grads['db1']
    dW2 = grads['dW2']
    db2 = grads['db2']
    ## END CODE HERE ###
    
    # Update rule for each parameter
    ### START CODE HERE ### (≈ 4 lines of code)
    W1 = W1 - learning_rate * dW1
    b1 = b1 - learning_rate * db1
    W2 = W2 - learning_rate * dW2
    b2 = b2 - learning_rate * db2
    ### END CODE HERE ###
    
    parameters = {"W1": W1,
                  "b1": b1,
                  "W2": W2,
                  "b2": b2}
    
    return parameters

测试一下

parameters, grads = update_parameters_test_case()
parameters = update_parameters(parameters, grads)

print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))

运行结果

W1 = [[-0.00643025  0.01936718]
 [-0.02410458  0.03978052]
 [-0.01653973 -0.02096177]
 [ 0.01046864 -0.05990141]]
b1 = [[ -1.02420756e-06]
 [  1.27373948e-05]
 [  8.32996807e-07]
 [ -3.20136836e-06]]
W2 = [[-0.01041081 -0.04463285  0.01758031  0.04747113]]
b2 = [[ 0.00010457]]

4.4把4.1,4.2,4.3整合到nn_model()

把你的NN模型整合到nn_model()

说明：NN模型必须以正确的顺序使用先前的函数。

代码如下

# GRADED FUNCTION: nn_model

def nn_model(X, Y, n_h, num_iterations=10000, print_cost=False):
    """
    Arguments:
    X -- dataset of shape (2, number of examples)
    Y -- labels of shape (1, number of examples)
    n_h -- size of the hidden layer
    num_iterations -- Number of iterations in gradient descent loop
                               梯度下降循环中的迭代次数
    print_cost -- if True, print the cost every 1000 iterations
                           如果为True，则每1000次迭代打印一次成本数值
    
    Returns:
    parameters -- parameters learnt by the model. They can then be used to predict.
                          模型学习的参数，它们可以用来进行预测
    """
    
    np.random.seed(3)
    n_x = layer_sizes(X, Y)[0]
    n_y = layer_sizes(X, Y)[2]
    
    # Initialize parameters, then retrieve W1, b1, W2, b2. Inputs: "n_x, n_h, n_y". Outputs = "W1, b1, W2, b2, parameters".
    ### START CODE HERE ### (≈ 5 lines of code)
    parameters = initialize_parameters(n_x, n_h, n_y)
    W1 = parameters['W1']
    b1 = parameters['b1']
    W2 = parameters['W2']
    b2 = parameters['b2']
    ### END CODE HERE ###
    
    # Loop (gradient descent)

    for i in range(0, num_iterations):
         
        ### START CODE HERE ### (≈ 4 lines of code)
        # Forward propagation. Inputs: "X, parameters". Outputs: "A2, cache".
        A2, cache = forward_propagation(X, parameters)
        
        # Cost function. Inputs: "A2, Y, parameters". Outputs: "cost".
        cost = compute_cost(A2, Y, parameters)
 
        # Backpropagation. Inputs: "parameters, cache, X, Y". Outputs: "grads".
        grads = backward_propagation(parameters, cache, X, Y)
 
        # Gradient descent parameter update. Inputs: "parameters, grads". Outputs: "parameters".
        parameters = update_parameters(parameters, grads)
        
        ### END CODE HERE ###
        
        # Print the cost every 1000 iterations
        if print_cost and i % 1000 == 0:
            print ("Cost after iteration %i: %f" % (i, cost))

    return parameters

测试一下

X_assess, Y_assess = nn_model_test_case()

parameters = nn_model(X_assess, Y_assess, 4, num_iterations=10000, print_cost=False)
print("W1 = " + str(parameters["W1"]))
print("b1 = " + str(parameters["b1"]))
print("W2 = " + str(parameters["W2"]))
print("b2 = " + str(parameters["b2"]))

运行结果如下

1.py:136: RuntimeWarning: divide by zero encountered in log
  logprobs = np.multiply(np.log(A2), Y) + np.multiply((1 - Y), np.log(1 - A2))
C:\planar_utils.py:34: RuntimeWarning: overflow encountered in exp
  s = 1/(1+np.exp(-x))
W1 = [[-4.18494482  5.33220319]
 [-7.52989354  1.24306197]
 [-4.19295428  5.32631786]
 [ 7.52983748 -1.24309404]]
b1 = [[ 2.32926815]
 [ 3.7945905 ]
 [ 2.33002544]
 [-3.79468791]]
W2 = [[-6033.83672179 -6008.12981272 -6033.10095329  6008.06636901]]
b2 = [[-52.66607704]]

4.5预测

构建函数predict()，使用你的模型进行预测。利用前向传播获得预测结果。

预测公式
$$prediction=\{\begin{array}{ll}1,& \text{if activation > 0.5}\\ 0,& \text{otherwise}\end{array}$$

如果你想根据阈值设置矩阵X的项为0或者1 ，你可以用以下方式X_new = (X > threshold)

代码如下

# GRADED FUNCTION: predict

def predict(parameters, X):
    """
    Using the learned parameters, predicts a class for each example in X
                 使用学习的参数，为X中的每个样本预测一个分类
    
    Arguments:
    parameters -- python dictionary containing your parameters 
    X -- input data of size (n_x, m)
    
    Returns
    predictions -- vector of predictions of our model (red: 0 / blue: 1)
    """
    
    # Computes probabilities using forward propagation, and classifies to 0/1 using 0.5 as the threshold.
    ### START CODE HERE ### (≈ 2 lines of code)
    A2, cache = forward_propagation(X, parameters)
    predictions = np.round(A2)
    ### END CODE HERE ###
    
    return predictions

测试一下

parameters, X_assess = predict_test_case()

predictions = predict(parameters, X_assess)
print("predictions mean = " + str(np.mean(predictions)))

运行结果

predictions mean = 0.666666666667

现在我们终于可以运行整个模型，看看它在平面数据集上的性能如何。

运行代码

# Build a model with a n_h-dimensional hidden layer
parameters = nn_model(X, Y, n_h = 4, num_iterations=10000, print_cost=True)

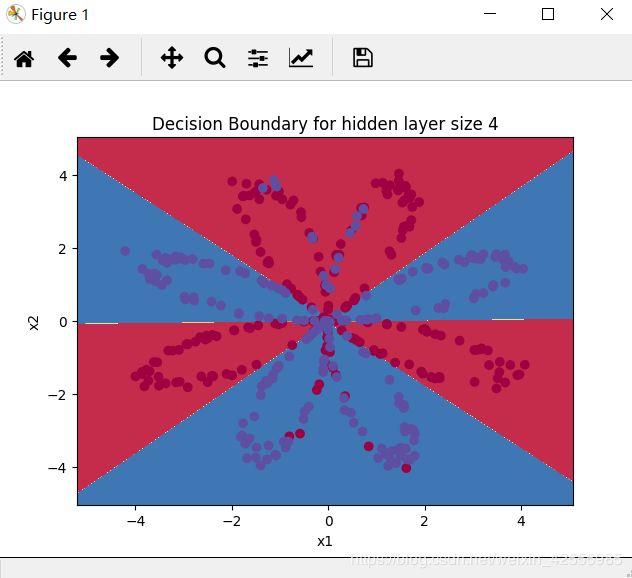
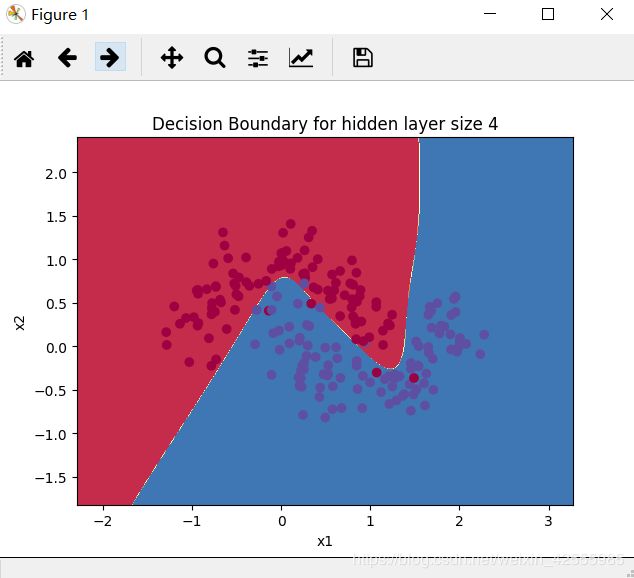
# Plot the decision boundary 绘制决策边界
plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y)
plt.title("Decision Boundary for hidden layer size " + str(4))
plt.show()

运行结果

Cost after iteration 0: 0.693048
Cost after iteration 1000: 0.288083
Cost after iteration 2000: 0.254385
Cost after iteration 3000: 0.233864
Cost after iteration 4000: 0.226792
Cost after iteration 5000: 0.222644
Cost after iteration 6000: 0.219731
Cost after iteration 7000: 0.217504
Cost after iteration 8000: 0.219504
Cost after iteration 9000: 0.218571

10000次迭代后，损失收敛。

分类结果如下图

对比原图

分类效果还是不错的。

再来看看准确率

# Print accuracy
predictions = predict(parameters, X)
print ('Accuracy: %d' % float((np.dot(Y, predictions.T) + np.dot(1 - Y, 1 - predictions.T)) / float(Y.size) * 100) + '%')

预测结果准确率为

Accuracy: 90%

对比逻辑回归线性模型分类的结果49%，准确率还是很高的。

单隐层NN模型准确学习到了花的叶子形状。不像逻辑回归模型，NN甚至可以学习高度非线性决策边界。

4.6调整隐藏层（单元）的数量

运行下面的代码，我们观察不同隐藏层（单元）数量模型的表现。

# This may take about 2 minutes to run

plt.figure(figsize=(16, 32))
hidden_layer_sizes = [1, 2, 3, 4, 5, 20, 50]
for i, n_h in enumerate(hidden_layer_sizes):
    plt.subplot(5, 2, i + 1)
    plt.title('Hidden Layer of size %d' % n_h)
    parameters = nn_model(X, Y, n_h, num_iterations=5000)
    plot_decision_boundary(lambda x: predict(parameters, x.T), X, Y)
    predictions = predict(parameters, X)
    accuracy = float((np.dot(Y, predictions.T) + np.dot(1 - Y, 1 - predictions.T)) / float(Y.size) * 100)
    print ("Accuracy for {} hidden units: {} %".format(n_h, accuracy))
plt.show()

运行结果如下

Accuracy for 1 hidden units: 67.5 %
Accuracy for 2 hidden units: 67.25 %
Accuracy for 3 hidden units: 90.75 %
Accuracy for 4 hidden units: 90.5 %
Accuracy for 5 hidden units: 91.25 %
Accuracy for 20 hidden units: 90.0 %
Accuracy for 50 hidden units: 90.75 %

说明：

• 较大的模型（具有更多隐藏单元）能够更好地拟合训练集，直到最终出现大模型过度拟合数据。
• 最佳的隐藏层单元数看上去应该是n_h = 5。事实上，它可以很好的拟合数据，也不会出现过拟合现象。
• 后面会学习的正则化，它允许我们使用非常大的模型（如n_h = 50），而不会出现太多过拟合。

7种隐藏单元数量的分类效果如下

总结

到现在为止，你已经学习了

• 构建一个完整的单隐层NN
• 很好的利用了一个非线性单元（激活函数tanh）
• 实现前向传播和反向传播，训练NN
• 观察隐藏单元数量变化的影响，例如：过拟合

5.单隐层NN模型在其他数据集上的表现

在planar_utils.py中还有其他几个数据集，如果你有兴趣，可以单隐层NN在不同数据集上的表现

把代码中原来加载数据集的代码

X, Y = load_planar_dataset()

替换为

# Datasets
noisy_circles, noisy_moons, blobs, gaussian_quantiles, no_structure = load_extra_datasets()

datasets = {"noisy_circles": noisy_circles,
            "noisy_moons": noisy_moons,
            "blobs": blobs,
            "gaussian_quantiles": gaussian_quantiles}

### START CODE HERE ### (choose your dataset)
dataset = "noisy_moons"
### END CODE HERE ###

X, Y = datasets[dataset]
X, Y = X.T, Y.reshape(1, Y.shape[0])

一共有4个数据集。这里我们尝试noisy_moons，如下图

• 数据集基本情况如下

The shape of X is: (2, 200)
The shape of Y is: (1, 200)
I have m = 200 training examples!

使用ML的逻辑回归算法分类结果如下

• 线性逻辑归回分类准确率

逻辑回归的准确率： 86 % (正确标签的数据点所占的百分比)

由于数据点在平面上的分布比“花”图案要更加接近上下两分，所以线性分类的准确率要比“花”数据集高。

• 使用noisy_moon数据集训练NN的模型结构是一样的。

The size of the input layer is: n_x = 5
The size of the hidden layer is: n_h = 4
The size of the output layer is: n_y = 2

• 迭代10000次训练后的预测分类效果如下
  

显然是非线性的分类。

• 损失情况

Cost after iteration 0: 0.693001
Cost after iteration 1000: 0.316565
Cost after iteration 2000: 0.316976
Cost after iteration 3000: 0.316195
Cost after iteration 4000: 0.099362
Cost after iteration 5000: 0.094746
Cost after iteration 6000: 0.093921
Cost after iteration 7000: 0.093484
Cost after iteration 8000: 0.093183
Cost after iteration 9000: 0.093096

• 单隐层NN(4个神经元)预测准确率

Accuracy: 96%

• 不同数量隐藏单元预测准确率

Accuracy for 1 hidden units: 86.0 %
Accuracy for 2 hidden units: 88.0 %
Accuracy for 3 hidden units: 97.0 %
Accuracy for 4 hidden units: 96.5 %
Accuracy for 5 hidden units: 96.0 %
Accuracy for 20 hidden units: 86.0 %
Accuracy for 50 hidden units: 86.0 %

6.完整代码

全部代码下载链接