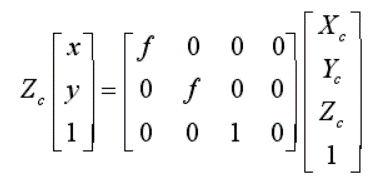雷达摄像头融合

简介

雷达信息和图像信息需要统一在同一空间和时间维度中才能进行数据融合计算，因此需要将毫米波雷达探测目标的坐标系转换到相机采集到的图像坐标系中，同时对毫米波雷达和相机的采样频率进行统一。

1.雷达

雷达能够连续不断地跟踪目标，并精确测量目标的位置(距离、方位角和俯仰角)。雷达通过天线技术实现目标角度测量，利用角随动系统驱动天线波束跟随目标运动，并通过角度传感器得到天线波束的角度信息。根据原理的不同，角度测量主要分为两种方法：振幅法和相位法。振幅法利用天线收到的回波信号的幅度值进行测量；相位法根据回波信号之间的相位差进行角度测量。雷达的测距原理较测角原理相对简单的多，天线发射高频脉冲，如果它的传播方向上有目标存在，则目标反射回波，并被雷达接收。假设目标与雷达的距离为R ，回波信号滞后于发射的脉冲信号时间为t ，则电磁波传播的距离等于光速乘以传播时间，即为： 

                                                                                                                                                                                

那么探测的目标距离为:

                                                                                                                                                                              

2.几种坐标系的介绍

2.1.世界坐标系

世界坐标系的引入是为了描述不同传感器之间的相对位置关系，因为数码相机安放在三维空间中，我们需要世界坐标系这个基准坐标系来描述数码相机的位置，并且用它来描述安放在此三维环境中的其它任何物体的位置，用（Xw, Yw, Zw）表示其坐标值。世界坐标系的位置由用户自定义设置。

2.2.毫米波坐标系

即雷达探测显示的目标方位信息，包括距离R，俯仰角，水平方位角

2.3.相机坐标系

以相机的光心为坐标原点，X 轴和Y 轴分别平行于图像坐标系的 X 轴和Y 轴，相机的光轴为Z 轴，用（Xc, Yc, Zc）表示其坐标值。

2.4.图像坐标系

以CCD 图像平面的中心为坐标原点，X轴和Y 轴分别平行于图像平面的两条垂直边，用( x , y )表示其坐标值。图像坐标系是用物理单位（例如毫米）表示像素在图像中的位置。

2.5.像素坐标系

以 CCD 图像平面的左上角顶点为原点，X 轴和Y 轴分别平行于图像坐标系的 X 轴和Y 轴，用(u , v )表示其坐标值。数码相机采集的图像首先是形成标准电信号的形式，然后再通过模数转换变换为数字图像。每幅图像的存储形式是M × N的数组，M 行 N 列的图像中的每一个元素的数值代表的是图像点的灰度。这样的每个元素叫像素，像素坐标系就是以像素为单位的图像坐标系

3.几种坐标系的相互转换

•毫米波雷达坐标系与世界坐标系转换

     以行车为例，在前向障碍物探测应用中，当毫米波雷达按要求安装在车辆前保险杠中间位置时，其雷达波探测面近似为一个二维水平平面。XOZ为世界坐标系所在平面， XrOrZr 是雷达坐标系所在平面，二者平行，Y，Yr垂直于XOZ平面，且XO0Z 平面与 XrOrZr 平面距离为 H，从而对于雷达探测到的目标 P(R, α)而言，转换到世界坐标系下的坐标为：

 

                          

•相机坐标系与图像坐标系转换

世界坐标系与相机坐标系的转换可以通过线性相机模型，即小孔成像模型得到.模型中共包含世界坐标系、相机坐标系、图像坐标系和像素坐标系共 4类坐标系.如下图所示：

                                                                                         

根据线性相机模型，通过三角相似关系可以获得相机坐标系与图像坐标系之间的转换关系，假设相机坐标系中有一点 P，坐标为(Xc, Yc, Zc)，P 点在图像平面的投影点为 P’，P’在图像坐标系中的坐标为(x, y)，且 P 点与 P’点的连线与相机镜头平面的交点为 Oc，即镜头光心。由于图像平面与相机镜头平面距离为相机焦距 f，因此通过三角相似原理可得：

转换成矩阵形式为：

•图像坐标系于像素坐标系的转化

      每幅数字图像在计算机内为M∗NM∗N数组，MM行NN列的图像中的每一个元素（称为像素，pixel）的数值即是图像点的灰度值。如图所示，在图像中定义直角坐标系u,v，每一像素的坐标(u,v)分别是该像素在数组中的列数和行数。所以（u,v)是以像素为单位的图像坐标系坐标。由于(u,v)只表示像素位于数组中的行数和列数，并没有用物理单位表示出该像素在图像中的位置。所以建立以物理单位（如毫米）表示的图像坐标系的坐标。图像中任意一个像素在这两个坐标的关系为：

                 

转换成矩阵形式为：

 

•世界坐标系于相机坐标系的转化

由于相机坐标系的位置固定在相机上，也存在于三维世界空间中，且坐标单位也为物理长度单位，其与世界坐标系只存在位置上的差异，因此可以通过建立旋转矩阵 R 和平移矩阵 T 实现世界坐标系与相机坐标系之间的转换。假设空间中一点 P 在世界坐标系中的坐标（Xw,Yw,Zw),则 P 点在相机坐标系下的坐标（Xc,Yc,Zc)为:

旋转矩阵 R 是 3×3 的单位正交矩阵，描述两个坐标系坐标轴之间的旋转关系，平移矩阵 T 是三维平移向量，描述两个坐标系原点之间的平移关系，OT=[0 0 0]为三维零向量，M1 为 4×4 矩阵，用于表示两个坐标系之间的旋转和平移关系.

•世界坐标系与像素坐标系的转换

     以上便得到了世界坐标系与相机坐标系转换关系、相机坐标系与图像坐标系转换关系、图像坐标系与像素坐标系转换关系，结合这三个转换关系，可以得到世界坐标系中一点P（Xw,Yw,Zw)在像素坐标系的转换关系为：

M 为投影矩阵，用于描述世界坐标系与像素坐标系的转换关系，其中M2为相机内部参数，M1为相机外部参数，有摄像机制造工艺决定。 当世界坐标系中的点向像素坐标系投影时，像素坐标系中只有唯一的点与之对应，但对于像素坐标系中的点而言，世界坐标系中有无数的点与之对应。因此，对于像素坐标中的已知点而言，必须对该点所在三维空间中的对应的基准点或参考平面进行规定，才能实现该点在世界坐标系中对应点的唯一确立。

4.雷达与摄像机信息融合

将毫米波雷达探测到的空间中一点，准确投影到相机采集到的图像平面中的点上，涉及到毫米波雷达坐标系、世界坐标系、相机坐标系、图像坐标系和像素坐标系共五个坐标系之间的转换。通过计算机视觉理论和相机模型，可得到与相机有关的四个坐标系之间的转换关系，并借助张正友相机标定法，获得转换关系中的相机内部参数与外部参数值，从而实现雷达坐标系到像素坐标系的转换。

1.雷达与相机坐标系
          

 2.相机与图像坐标系

使用图像去畸变

3.图像与像素坐标系

联合以上四式便可得到雷达到像素坐标系的空间位置信息转换。

5.具体实现

雷达与摄像头处于同一竖直平面上，摄像头距离雷达高度为2.85m,人的高度为1.8米,雷达探测的人与雷达的距离从10米到80米，每次检测间隔10米，以下的结果较好的验证了雷达与摄像头融合的效果，能较精确的确定目标在摄像头所拍摄的图片的像素位置。