单神经元PID控制+Simulink控制系统仿真
最近在学习基于神经网络的电机智能控制,神经网络与PID有两种结合方式:采用单神经元结构,神经元输入权值一一对应PID的三个参数,神经元的输入值为经过比例、积分和微分处理后的偏差值;另一种是在常规PID控制器的基础上增加一个神经网络,用神经网络在线调节PID的三个参数。
关于神经网络的相关知识网上有很多详细的介绍,在此不展开介绍了。单神经元PID控制框图如下图所示:
控制算法为:
在实际应用中都使用改进的控制算法,如下所示:
Matlab Simulink仿真建模
首先是连续控制系统的仿真,被控对象的传递函数为:G(s)=1/(20s+1),模型如下图所示:
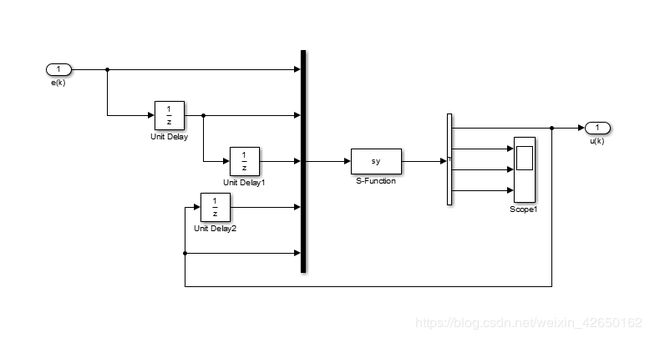
输入为阶跃信号,其参数为默认值,一个简单的闭环控制系统。单神经元PID控制器的内部结构如下图所示:
误差信号e(k)经过一个延迟环节1/z变为e(k-1),故S-function的五个输入为:e(k),e(k-1),e(k-2),u(k-1),u(k)。在S函数中输入表示为矩阵的形式:u=[e(k);e(k-1);e((k-2);u(k-1);u(k)]=[u(1);u(2);u(3);u(4);u(5)]。
关于S-function的使用方法,请参考我写的另一篇博客:
https://blog.csdn.net/weixin_42650162/article/details/90488610
下面是S-function编写实现控制算法(改进后的控制算法):
function [sys,x0,str,ts,simStateCompliance] = sy(t,x,u,flag,deltak,K)
%输入两个外部参数 deltak,K 这里deltak是个列向量deltak=[ni;np;nd],表示学习算法中的
%积分、比例、微分学习速率
switch flag,
case 0,
[sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes;
%调用初始化函数
case 2,
sys=mdlUpdate(t,x,u,deltak);
%更新状态变量,此算法有三个状态变量,三个权值系数w1(k),w2(k),w3(k)
case 3,
sys=mdlOutputs(t,x,u,K);
%调用输出函数,输出控制值信号
case {1,4,9},
sys=[];
otherwise
DAStudio.error('Simulink:blocks:unhandledFlag', num2str(flag));
end
function [sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes
%初始化函数
sizes = simsizes;
sizes.NumContStates = 0;
sizes.NumDiscStates = 3;
%定义三个离散的状态变量,w1(k),w2(k),w3(k)
sizes.NumOutputs = 4;
%定义四个输出,算法中的控制变量u(k)和三个PID参数Kp,Ki,Kd
sizes.NumInputs = 5;
%定义该系统有五个输入
sizes.DirFeedthrough = 1;
%直接馈通,输出和输入有关存在直接馈通参数为1
sizes.NumSampleTimes = 1;
%采样时间个数,默认值
sys = simsizes(sizes);
x0 = [0.1,0.1,0.1];
%定义三个状态变量的初始值,即w1(0)=0.1,w2(0)=0.1,w3(0)=0.1
str = [];
ts = [-1 0];
%S-function设置为[-1 0]为按照其所连接块的速率来运行
simStateCompliance = 'UnknownSimState';
function sys=mdlUpdate(t,x,u,deltak)
%状态更新函数
sys = x+deltak*u(1)*u(5)*(2*u(1)-u(2));
%此处表示三个状态变量的更新公式,x为现在的状态变量x=[w1(k);w2(k);w3(k)]
%即sys=[w1(k+1);w2(k+1);w3(k+1)]=
%[w1(k)+ni*u(1)*u(5)*(2*u(1)-u(2));w2(k)+np*u(1)*u(5)*(2*u(1)-u(2));
%w3(k)+nd*u(1)*u(5)*(2*u(1)-u(2))]
%输入变量u=[u(1);u(2);u(3);u(4);u(5)]=[e(k);e(k-1);e(k-2);u(k-1);u(k)]
function sys=mdlOutputs(t,x,u,K)
%输出函数
xx = [u(1) u(1)-u(2) u(1)+u(3)-2*u(2)];
%xx=[x1(k) x2(k) x3(k)],对应学习算法中的三个xi(k)
sys = [u(4)+K*xx*x/sum(abs(x));K*x/sum(abs(x))];
%计算输出sys=[u;Ki;Kp;Kd]=[u(4)+K(w1'(k)*x1(k)+w2'(k)*x2(k)+w3'(k)*x3(k));
%K*w1(k)/(abs(w1(k))+abs(w2(k))+abs(w3(k));K*w2(k)/(abs(w1(k))+abs(w2(k))+abs(w3(k));
%Kw3(k)/(abs(w1(k))+abs(w2(k))+abs(w3(k))]
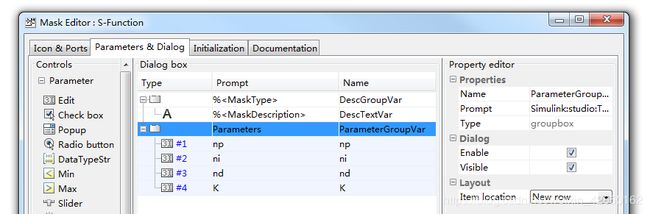
对S-function模块进行封装,具体过程参考我的另一篇博客:
https://blog.csdn.net/weixin_42650162/article/details/90488610
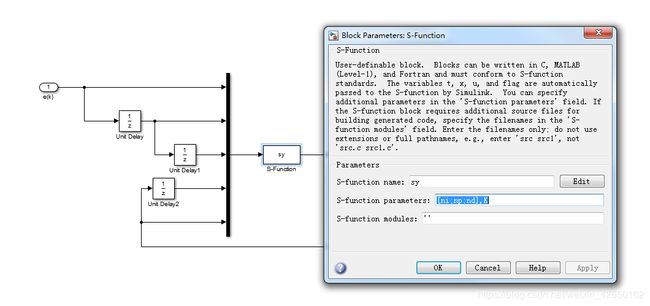
点击S-function模块进行参数设置,如下图所示:
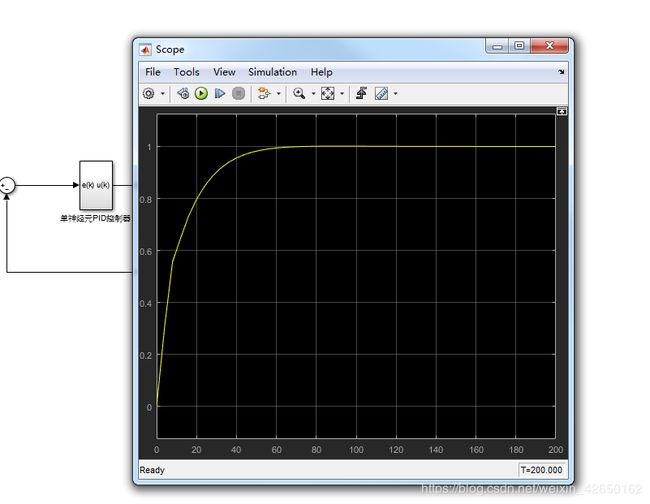
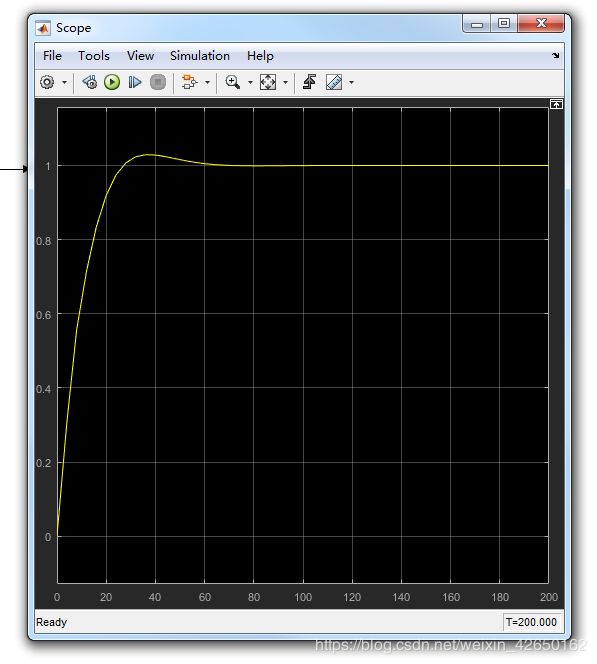
学习参数设置为上述所示,仿真结果如下:
学习参数调节好,仿真结果还是很好的。
有监督Hebb学习规则,没有改进的仿真算法:
function [sys,x0,str,ts,simStateCompliance] = sy1(t,x,u,flag,ni,np,nd,K)
switch flag,
case 0,
[sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes;
case 2,
sys=mdlUpdate(t,x,u,ni,np,nd);
case 3,
sys=mdlOutputs(t,x,u,K);
case {1,4,9},
sys=[];
otherwise
DAStudio.error('Simulink:blocks:unhandledFlag', num2str(flag));
end
function [sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes
sizes = simsizes;
sizes.NumContStates = 0;
sizes.NumDiscStates = 3;
sizes.NumOutputs = 4;
sizes.NumInputs = 5;
sizes.DirFeedthrough = 1;
sizes.NumSampleTimes = 1;
sys = simsizes(sizes);
x0 = [0.1,0.1,0.1];
str = [];
ts = [-1 0];
simStateCompliance = 'UnknownSimState';
function sys=mdlUpdate(t,x,u,ni,np,nd)
sys = x+[ni*u(1)*u(5)*u(1);np*u(1)*u(5)*(u(1)-u(2));nd*u(1)*u(5)*(u(3)-2*u(2))];
function sys=mdlOutputs(t,x,u,K)
xx = [u(1) u(1)-u(2) u(1)+u(3)-2*u(2)];
sys = [u(4)+K*xx*x/sum(abs(x));K*x/sum(abs(x))];
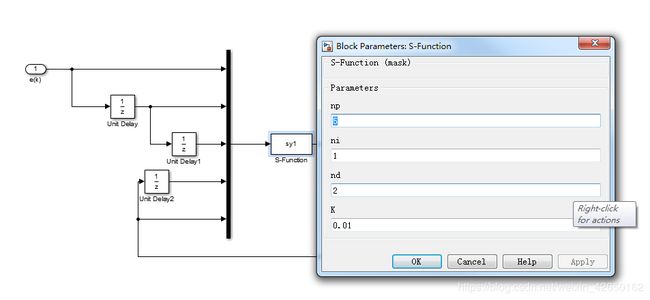
进行封装,如下图所示
点击S-function模块进行参数设置,如下图所示:
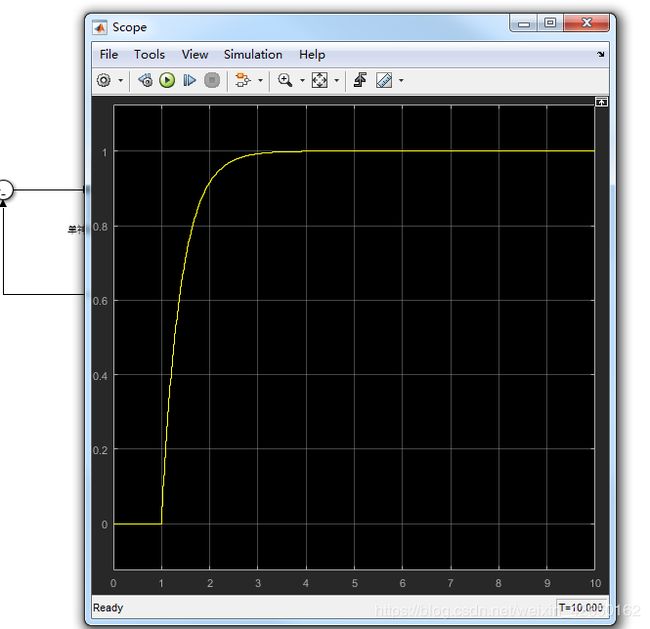
仿真结果如下:
设置同样的学习参数,改进后的控制算法明显优于改进前的控制的算法。以上为单神经元PID控制系统仿真,仿真模型S函数等资源已上传,可自行下载:
https://download.csdn.net/download/weixin_42650162/11215460
https://download.csdn.net/download/weixin_42650162/11215448
离散系统仿真:离散系统的传递函数为G(z)=(0.1z+0.623)/(z^2-0.368z-0.26)
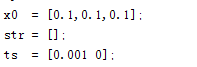
S-function初始化函数中的采样时间由[-1 0],改为ts=[0.001 0]
采用改进前的算法,学习参数设置如下:
仿真结果如下:
采用改进后的算法同样的参数仿真如下:
同样的学习参数,离散系统改进前的比改进后的仿真结果要好
关于离散系统的单神经元PID控制系统的仿真模型以及S函数已上传,如有需要可自行下载:
https://download.csdn.net/download/weixin_42650162/11234370
https://download.csdn.net/download/weixin_42650162/11234373
注:离散系统要采用固定步长仿真