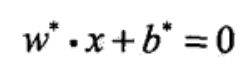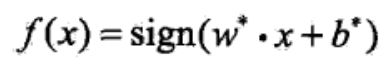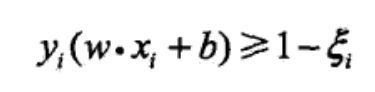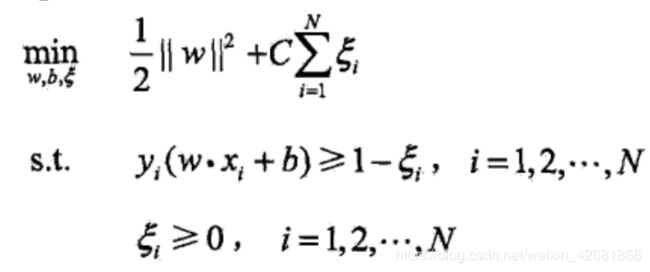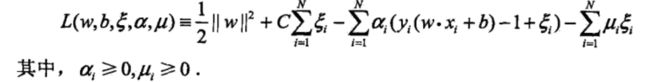读书笔记-统计学习方法（李航） 第七章

7.1 线性可分支持向量机与硬间隔最大化

支持向量机是一种二分类模型，它的基本模型是定义在特征空间上的间隔最大的，
间隔最大使它区别于感知机。
支持向量机还包括核技巧，这使它成为实质上的非线性分类器。
学习策略可以形式化为求解凸二次规划问题，或者等价于 最小化合页损失

分离超平面：

决策函数：

函数间隔：

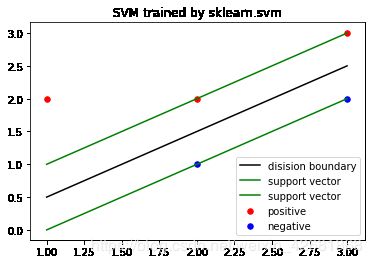
几何间隔：

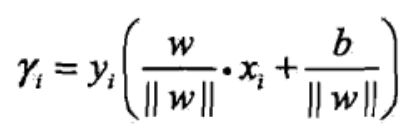
原始目标函数：
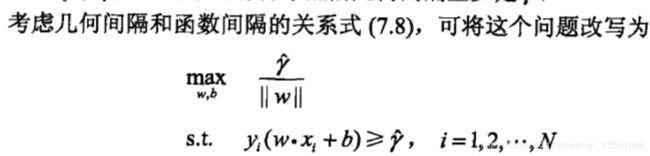上式中的函数距离不影响最优化问题的解（例如一个正实例点的特征带入决策函数：w·x+b = y> 0, 等比例缩放b和w为原来的k倍，kw·x + kb = ky > 0依旧成立。所以可以通过调整k值同时缩放w和b使得约束条件右边的函数距离ky = 1。ps:问题：学习过程的最终结果同样会改变w和b，为什么缩放对结果没影响，而学习过程是有影响并会得到一个有效的决策函数呢？答：缩放体现在决策函数w`x+b上不改变决策函数结果的正负性，而学习过程中w和b不是同比例缩放的，而是遵循让某些点的（w·x +b）=1的约束条件下进行改变的）
确定可以令函数距离=1之后，目标函数就变成这样：（取倒数和乘0.5是为了求导方便）
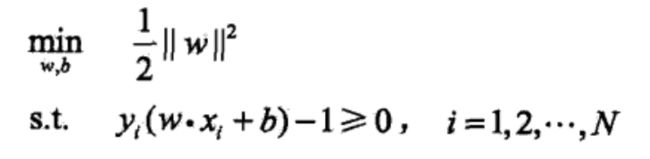支持向量之间的距离为：

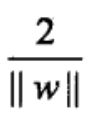
然后对目标函数构建拉格朗日函数：
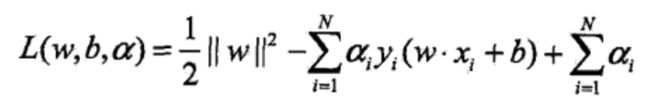求得拉格朗日是式子取到极致的拉格朗日乘子向量 a* = (a1,a2,a3…an),这里面的乘子有很多0，支持向量外的点，乘子a不等于0的点就是支持向量。最终的决策函数就变成：

---

7.2 线性支持向量机与软间隔最大化

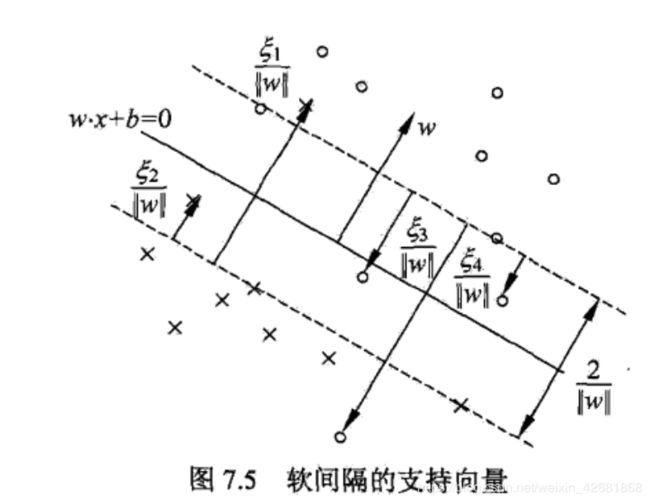
为了解决线性不可分问题（有坏点）引入软间隔，给每个样本点引入松弛变量，使函数间隔加上松弛变量 >=1。

约束条件变为：

目标函数变为：

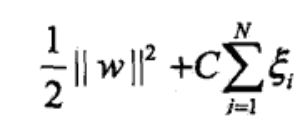
C是对松弛变量的惩罚参数，C越大对误分类点的惩罚就越大，C越小对误分类点的惩罚就越小。
所以新目标函数的最小化是要求：
1：支持向量的距离尽量远，函数间隔大。
2：同时函数间隔中间部分的点尽量少（会被惩罚）。
C是调和这两项的系数，需要在实践中去搜索查找

根据目标函数的约束条件：
构建拉格朗日函数：

软间隔支持向量机结果示意图：

上文的目标都是间隔最大，如果把目标换成损失最小，并且为了区别于感知机的只对误分类设定loss，合页损失对即使正确分类，但是非常靠近决策边界的点也要惩罚（合页损失对分类有更高的要求）。合页损失如下（这里的w是L2范数，正则化项）：

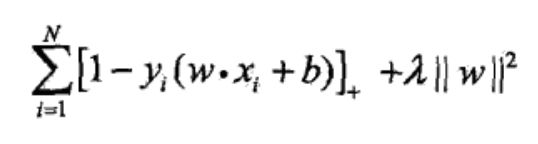
合页损失示意图：
合页损失最小化过程的最终化简加过和最大化间隔是一样的。

---

7.3 非线性支持向量机与和函数

核技巧就是通过映射的方式把原特征映射到高维特征空间中，使原本不是线性问题的问题在高维空间变成线性问题。

常用核函数：
1：多项式核函数：


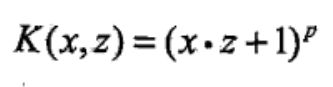
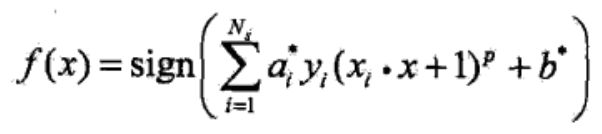
2：高斯核函数：


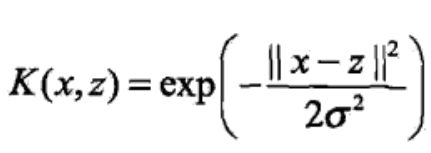
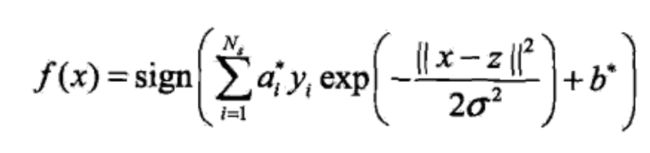
3：字符串核函数：

---

7.4 序列最小最优化算法

为了简化最优化过程中大量的拉格朗日算子的计算。序列最小化可以帮助我们去逼近最优化的a*,
通过同时改变两个ai,aj(因为sum(yiai)=0的约束条件下，必须至少同时改变两个参数)，同时改变两个参数达到此时其他参数不变的情况下的最优（局部），然后不断的选点-局部最优-选点-局部最优。。。，去逼近全局最优的a*。

---

实战：

"""
作业7

1：已知正例点（1，2），（2，2），（3，3），负例点（2，1），（3，2），试求最大间隔分离超平面，间隔边界，及支持向量。
2：调用sklearn 中的svm，尝试改变参数如C ,kernel

"""

#训练数据集
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# import sympy
import random
# %matplotlib
train = np.array([
    [1,2],
    [2,2],
    [3,3],
    [2,1],
    [3,2],
])
y = np.array([1,1,1,-1,-1])

fig = plt.figure()
plt.scatter(train[:3,0],train[:3,1],c="red",s=30)
plt.scatter(train[3:,0],train[3:,1],c="blue",s=30)
plt.show()

"""
假设分类超平面为: w1 * x1 + w2 * x2 + b = 0
支持面就是：
    w1 * x1 + w2 * x2 + b + 1 = 0
    w1 * x1 + w2 * x2 + b - 1 = 0
    
那么决策函数就是 sign(w1 * x1 + w2 * x2 + b)   (=1 if >0 else = -1)

学习过程：
    目标函数：min(1/2*||w||2)   ps:变量是w
    约束条件：yi(w·xi +b -1 ) >= 0
    
    令a1,a2,a3...a5是大于等于0的系数
    原问题等价于对偶问题 min( 0.5 * sumsum(ai * aj * yi* yj *(x·xi) )  +  sum(ai))    ps:变量是拉格朗日系数a
    约束条件：sum(ai*yi)=0 , ai>=0
    
    解出最优解a_ = (a1_, a2_, a3_ ,a4_, a5_) 之后
    w_ = sum(ai * yi * xi)
    b_ = yj - sum(ai * yi(xi · xj))   ps: (即随便选一个a不为0的点j（决策向量）带入 w_ 的决策函数中，得到b)
    
"""
print(train)
print(y)

[[1 2]
 [2 2]
 [3 3]
 [2 1]
 [3 2]]
[ 1  1  1 -1 -1]

def svmSimpleSMO(train,y,C,toler,maxIter):
    """
    伪代码(参考：机器学习实战)：
    创建一个a向量并将其初始化为0向量
    当迭代次数小于最大迭代次数时（外循环），
        对数据集中每个数据向量（内循环）:
            若该数据向量可以被优：
                随机选择另外一个向量，
                同时优化这两个向量。
                如果这两个向量都不能被优化，退出内循环。
            如果所有向量都没有被优化，增加迭代数目
    """
    
    #辅助函数
    m = train.shape[0]
    n = train.shape[1]

    def selecJrand(i,m):
        j = i
        while j==i:
            j = int(random.uniform(0,m))
        return j
    
    def clipAlpha(aj,H,L):
        if aj > H:
            aj = H
        if L > aj:
            aj = L
        return aj
    
    #主函数
    dataMatrix = np.mat(train)
    labelMat = np.mat(y).transpose()
    alphas = np.mat(np.zeros((m,1)))       #初始化alpha
    b = 0                    #初始化b
    iter = 0                   #迭代次数

    while iter < maxIter:      
        alphaPairChanged = 0
        for i in range(m):     #遍历每个数据点
            #预测的类别
            fxi = float(np.multiply(alphas ,labelMat).T * (dataMatrix * dataMatrix[i,:].T) ) + b 
            #误差
            Ei = fxi - float(labelMat[i])                                                         
            #如果误差很大，对对应的alpha进行优化
            if ((labelMat[i]*Ei < -toler) and (alphas[i]<C))  or \
               ((labelMat[i]*Ei > toler) and (alphas[i]>0)):
                j = selecJrand(i,m)   #随机选择第二个点j
                fxj = float(np.multiply(alphas ,labelMat).T * (dataMatrix * dataMatrix[j,:].T) ) + b #点j的预测值
                Ej = fxj - float(labelMat[j])  #点j的误差
                alphaIold = alphas[i].copy()
                alphaJold = alphas[j].copy()

                
                #分两种情况讨论：
                if labelMat[i] != labelMat[j]:
                    L = max(0,alphas[j] - alphas[i])
                    H = min(C,C + alphas[j] - alphas[i])
                else:
                    L = max(0,alphas[j] + alphas[i] - C)
                    H = min(C,alphas[j] + alphas[i])
                    
                if (L==H):     #如果alpha[j]的下界等于上界，跳出次此内循环，不优化alpha
                    print("L==H")
                    continue 
                
                
                #alpha[j]的最优修改量 eta
                eta = 2.0 * dataMatrix[i,:] * dataMatrix[j,:].T - \
                            dataMatrix[i,:] * dataMatrix[i,:].T - \
                            dataMatrix[j,:] * dataMatrix[j,:].T
                
                if eta >= 0:   #这里是简化的点******=====---
                    print("eta >= 0")
                    continue 
                
                # 更新alpha
                alphas[j] -= labelMat[j] * (Ei-Ej) / eta

                alphas[j] = clipAlpha(alphas[j],H,L)   #把超出边界的部分拉回到边界上
                if abs(alphas[j]-alphaJold) < 0.0001:
                    print("j 变化太小")
                    continue
                alphas[i] += labelMat[j]*labelMat[i] * (alphaJold-alphas[j])
                
                #更新b
                b1 = b - Ei - \
                     labelMat[i] * (alphas[i]-alphaIold) * dataMatrix[i,:]*dataMatrix[i,:].T - \
                     labelMat[j] * (alphas[j]-alphaJold) * dataMatrix[i,:]*dataMatrix[j,:].T
                b2 = b - Ej - \
                     labelMat[i] * (alphas[i]-alphaIold) * dataMatrix[i,:]*dataMatrix[j,:].T - \
                     labelMat[j] * (alphas[j]-alphaJold) * dataMatrix[j,:]*dataMatrix[j,:].T
                if (0<alphas[i]) and (alphas[i]<C):
                    b = b1
                elif (0<alphas[j]) and (alphas[j]<C):
                    b = b2
                else:
                    b = (b1+b2)/2.0
                
                #更新迭代状态
                alphaPairChanged += 1
                print("iter: %d i: %d, pairsChanged %d" % (iter,i,alphaPairChanged))
                
        if (alphaPairChanged==0): #没有更新参数，当没有更新参数的次数达到设定的最大值之后，退出外循环
            iter += 1
        else:                     #更新参数了，重新计算迭代次数
            iter = 0
        print("iteration number %d" % iter)
    
    return alphas,b
                    
        
    

C = 10 #惩罚参数
toler = 0.001 #容错率
maxIter = 20

alphas,b = svmSimpleSMO(train,y,C,toler,maxIter)

iter: 0 i: 0, pairsChanged 1
iter: 0 i: 1, pairsChanged 2
iter: 0 i: 2, pairsChanged 3
iter: 0 i: 3, pairsChanged 4
iter: 0 i: 4, pairsChanged 5
iteration number 0
iter: 0 i: 1, pairsChanged 1
j 变化太小
iter: 0 i: 4, pairsChanged 2
iteration number 0
iter: 0 i: 0, pairsChanged 1
j 变化太小
j 变化太小
iter: 0 i: 3, pairsChanged 2
j 变化太小
iteration number 0
iter: 0 i: 2, pairsChanged 1
j 变化太小
iteration number 0
iter: 0 i: 1, pairsChanged 1
iter: 0 i: 2, pairsChanged 2
iteration number 0
iteration number 1
iteration number 2
iteration number 3
iteration number 4
iteration number 5
iteration number 6
iteration number 7
iteration number 8
iteration number 9
iteration number 10
iteration number 11
iteration number 12
iteration number 13
iteration number 14
iteration number 15
iteration number 16
iteration number 17
iteration number 18
iteration number 19
iteration number 20

print(alphas)
print(b)
print(train)
print(np.multiply(alphas,np.mat(y).T) )
print((np.multiply(alphas,np.mat(y).T) ).T * train)
w = (np.multiply(alphas,np.mat(y).T) ).T * train
w = np.array(w)[0]
print("w = ",w)
b_ = float(b)
print("b = ",b_)
print(-(1*w[0]+b_)/w[1])

[[0.  ]
 [2.72]
 [1.28]
 [0.72]
 [3.28]]
[1.]
[[1 2]
 [2 2]
 [3 3]
 [2 1]
 [3 2]]
[[ 0.  ]
 [ 2.72]
 [ 1.28]
 [-0.72]
 [-3.28]]
[[-2.  2.]]
w =  [-2.  2.]
b =  1.0
0.5000000000000013

np.dot(train , w) + b

array([ 3.,  1.,  1., -1., -1.])

#画图
print(w,b_)
fig = plt.figure()
plt.scatter(train[:3,0],train[:3,1],c="red",s=30,label = "positive")
plt.scatter(train[3:,0],train[3:,1],c="blue",s=30,label = "negative")
x1 = list(range(1,4))
x2 = [-(x1_*w[0] + b_ )/w[1] for x1_ in x1]
x2_1 = [-(x1_*w[0] + b_ + 1)/w[1] for x1_ in x1]
x2_2 = [-(x1_*w[0] + b_ - 1)/w[1] for x1_ in x1]
plt.plot(x1,x2,c="black",label="disision boundary")
plt.plot(x1,x2_1,c="green",label = "support vector")
plt.plot(x1,x2_2,c="green",label = "support vector")
plt.legend()
plt.title("SVM trained by SmpleSMO")

# plt.show()

[-2.  2.] 1.0

#调包
from sklearn.svm import SVC
clf = SVC(C=10,kernel="linear")
clf.fit(train,y)
w = clf.coef_[0]
print(w)
b =clf.intercept_
print(b)

[-2.  2.]
[1.]

#画图
print(w,b)
fig = plt.figure()
plt.scatter(train[:3,0],train[:3,1],c="red",s=30,label = "positive")
plt.scatter(train[3:,0],train[3:,1],c="blue",s=30,label = "negative")
x1 = list(range(1,4))
x2 = [-(x1_*w[0] + b )/w[1] for x1_ in x1]
x2_1 = [-(x1_*w[0] + b + 1)/w[1] for x1_ in x1]
x2_2 = [-(x1_*w[0] + b - 1)/w[1] for x1_ in x1]
plt.plot(x1,x2,c="black",label="disision boundary")
plt.plot(x1,x2_1,c="green",label = "support vector")
plt.plot(x1,x2_2,c="green",label = "support vector")
plt.legend()
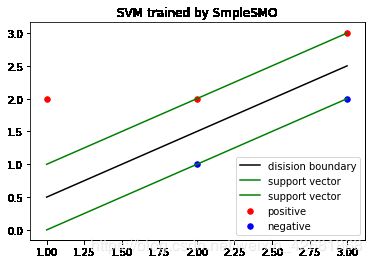
plt.title("SVM trained by sklearn.svm")
plt.show()

[-2.  2.] [1.]

结论：调包和simpleSMO结果差不多，关键在于C值的选择。