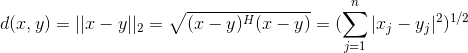读书笔记《矩阵分析与计算》by 李继根 张新发

注：本篇博文是自己在阅读《矩阵分析与计算》一书中的记录，不喜勿喷，请绕道！

矩阵是线性空间里的变换的描述。从更高的层面看，矩阵是泛函中的一种特殊的线性算子。一般可将矩阵的理论知识大致划分为“空间与变换”，“矩阵分解论”以及“矩阵分析论”，其中空间与变换依托的就是泛函分析与抽象代数。

第一章 线性方程组

1.2 矩阵的LU分解

例：求解线性方程组

形如L这样的对角元都为1的下三角矩阵称为单位下三角矩阵。

如果方阵A可以分解为单位下三角矩阵L与上三角矩阵U的乘积，即A=LU，称为A的LU分解，或三角分解。

（LU分解定理）如果n阶方阵A的各阶顺序主子式都不为0，即A的各阶顺序主子式矩阵都可逆，则存在唯一的单位下三角矩阵L与唯一的非奇异上三角矩阵U，使得A=LU。

（LDU分解定理）如果n阶方阵A的各阶顺序主子式都不为0，则存在唯一的单位下三角矩阵L与唯一的单位上三角矩阵U以及对角矩阵D，使得A=LDU。

1.2.2 特殊矩阵的LU分解

当A为n阶实对称正定矩阵时，其所有顺序主子式>0,因此，根据上文LDU分解定理，A=LDU。从而.

这里是单位下三角矩阵，是单位上三角矩阵。因为,故

由LU分解的唯一性，可知

即

更进一步，由于A为实对称正定矩阵，因此对角矩阵D的对角元都为正数，若记

则有

（Cholesky定理/平方根法）设A是实对称正定矩阵，则存在唯一的可逆下三角矩阵L，使得

（改进的平方根法）思考：根据，有

因此，可先解，再解,这种方法就避免了平方运算。这种改进的平方根法适用于任意对称矩阵（未必正定），除非出现主元为零的情况。

1.4 线性方程组的数值解法概述

线性方程组求解，最小二乘问题，特征值问题是矩阵计算的三大基本问题

 

第二章 线性空间与线性变换

2.1 从解空间到向量空间

AX=0的解称为一个解空间。

向量空间：如果V是n维列向量的非空集合。并且V对于加法和数乘这两种向量运算都封闭，那么就称集合V为向量空间。

注：（1）中不过原点的平面都不是向量空间。

        （2）若把向量空间V看做无穷个向量组成的向量组，那么V的基就是该向量组的极大无关组，V的维数就是该向量组的秩。

        （3）对而言，其0维子空间是零空间，其一维子空间是经过原点的任意直线，其二维子空间是经过原点的任意平面，其三维子空间是其自身。

2.2 线性空间

线性空间是向量空间在元素和线性运算上的推广和抽象，它的元素可以是向量，矩阵，多项式，函数等。它的线性运算既可以是我们熟悉的一般运算，也可以是各种特殊的运算，向量空间中的线性组合，线性相关，线性无关，基，坐标等定义和结论都可以推广到一般线性空间，尤其是坐标，能够将一般线性空间的问题转化成向量空间的问题。

2.2.2线性空间的概念及性质

注：（1）在线性空间V的定义中。不仅不再关心元素的特定属性，而且也不关心这些线性运算（即加法和数乘）的具体形式

        （2）数域被推广到了更一般的数域F，例如实数域和复数域，此时相应的线性空间分别被称为实空间和复空间

       （3）线性空间是线性代数的最基本概念之一，概括的说，它要求的是“两种封闭运算和八条运算规律”

       （4）再次强调：线性空间中的元素可以是向量，矩阵，多项式，函数等，其中的线性运算可以任意指定，而且同一个线性空间还可以指定不同的线性运算。

到此时才发现自己对“线性代数”中的“线性”完全没理解啊！！

2.2.4 线性空间的同构

（同态映射）设，是数域F上的两个线性空间，是到的映射（未必一一对应），如果对任意，和任意F,都有

（1）可加性：

（2）齐次性：

则称为到的同态映射，线性映射或线性算子。特别地，当为F时，称为上的线性泛函。当与是同一个线性空间时，称为上的自同态映射或线性变换。

（同构映射）设，是数域F上的两个线性空间，是到的同态映射，并且是一一对应的，则称为到的线性同构映射。同构映射是特殊的同态映射。

维数是有限维线性空间唯一的本质特征。

2.3 子空间的交与和

我们希望将一个高维线性空间分解为多个低维线性子空间的和，并通过对线性子空间的研究，更加深刻地揭示整个线性空间的结构。

2.4 线性变换及其矩阵表示

线性变换是线性空间的核心内容，反映的是线性空间中元素间的一种基本联系，体现出一种“动态的”或者“直观的”视角。借助基的概念，可在线性变换与矩阵之间建立一一对应关系，从而将线性变换的运算转化为矩阵的运算。

2.4.1 几个简单的线性变换

（旋转变换或Givens变换）将中的任意向量,绕原点逆时针旋转角至

则

   

（反射变换或Householder变换）

（伸缩变换）

（投影变换）

（微分变换）

（积分变换）

注：（1）平移变换不是线性变换，而伸缩变换，投影变换是线性变换。

        (2)将具体的矩阵与抽象的线性映射联系起来，从而将线性映射的运算转化为矩阵的数值计算。这中间的桥梁，就是与坐标轴类似的线性空间的基。

2.4.3 线性变换的矩阵表示

思考：为什么

分析：在中，记,显然当时，有

记为G，故,

退化到一维的情形。此时,

即

注：（1）同一个线性变换在不同基下的矩阵是相似的；反之，相似的两个矩阵可看成同一个线性变换在不同基下的矩阵。

（2）从变换角度理解特征值

定义：设是在数域F上线性空间V的一个线性变换，如果存在,及非零向量,使得

         则称为的特征值，称非零向量为的属于特征值的特征向量。

显然，特征向量经过变换以后，仍然与成倍数关系（倍数就是特征值），即线性相关或共线。

（3）对任一矩阵,矩阵的特征值的集合称为的谱（spectrum）,的特征值的模的最大值称为的谱半径。

2.5 矩阵的Jordan标准型

从逻辑上看，标准型的理论源自矩阵的相似性，因为相似矩阵有许多相似不变量：特征多项式，特征值（包括代数重数和几何重数），行列式，迹和秩等，并且特征向量也可以借助于可逆矩阵的相似变换矩阵互相求出，这自然导出了寻找相似矩阵集合中的“代表矩阵”的问题。“代表矩阵”当然越简单越好，对于可对角化矩阵。“代表矩阵”就是特征值组成的对角矩阵，但一般矩阵未必与对角矩阵相似。因此我们只能退而求其次，寻找“几乎对角的”矩阵，这就引出了矩阵在相似变换下的各种标准型问题，其中Jordan标准型是最接近对角的矩阵，因为除了对角元之外，它只在第1条对角线上另取0或1.

 

第三章 内积空间

在线性空间中，只涉及了向量的线性运算。可是在作为线性空间具体模型的向量空间中，还涉及向量的长度，夹角等度量性质，它们在解决几何问题时起着关键作用，因此必须把度量的概念引入到线性空间中来，以实现代数与几何的完美结合。

3.1 从向量空间到欧式空间

将3维空间中的点积推广到n维向量空间，就是向量的内积。为了区别于向量空间，称带有标准内积的向量空间为欧式空间。

3.2 QR分解

QR分解在矩阵计算中占据相当重要的地位，利用QR分解，可以解决各种应用中出现的最小二乘问题，特征值问题等矩阵计算中的核心问题。

设,,...是欧式空间的一组基，，,...是我们希望得到的正交基

、

重要思想：Schmidt过程实际上是逐步扩张正交向量组，使得

    

并且

使用矩阵语言，就是Q=AT

由于上三角矩阵的逆矩阵仍然是上三角矩阵，令R=,所以A=QR

（QR分解定义）对于n阶方阵A，如果存在正交矩阵Q和上三角矩阵R，使得A=QR，则称该式为A的完全QR分解。

3.3 欧式空间与其标准正交基

向量空间中向量的长度与夹角是用内积定义的，引入这些度量后的线性空间，自然就推广为内积空间。在内积空间内引入标准正交基后，向量的内积运算就转化成了我们熟悉的向量空间的内积运算。

注意：

（1）内积实际上是一种映射，是双线性函数，这样同一个线性空间显然可定义多种内积

（2）欧式空间仅仅是一种特殊的欧式空间

（3）由于向量的内积与向量的线性运算无关，所以欧式空间V实际上是特殊的线性空间V，即定义了内积的线性空间。

(希尔伯特空间定义)希尔伯特空间是所有平方和收敛的实数列的集合。

注：（1）在小波分析和有限元等学科中，小波基和有限元实际上也是相应欧式空间的正交基函数

      （2）矩阵分解为三角矩阵，对角矩阵，正交矩阵等特殊矩阵的乘机

3.6 酉空间，酉变换与酉矩阵

各类空间的层次关系

拓扑空间		线性空间
Hausdorff空间		拓扑线性空间
距离空间		距离线性空间		完备距离线性空间
		赋范空间		Banach空间
		内积空间		Hibert空间
				欧式空间

是矩阵的复共轭转置矩阵

称满足的矩阵为Hermite矩阵。

注：酉矩阵是正交矩阵的推广，Hermite矩阵是对称矩阵的推广。

 

第四章 特殊变换及其矩阵

例如：上三角矩阵，下三角矩阵，三对角矩阵，带状矩阵，对称矩阵，Hermite矩阵，正交矩阵，酉矩阵，正规矩阵，投影矩阵，Toeplitz矩阵，Frobenius矩阵，Vandermonde矩阵，Z矩阵，M矩阵，H矩阵，对角占优矩阵，非负矩阵，友矩阵，协方差矩阵，随机矩阵，Hamilton矩阵，辛矩阵，Hilbert矩阵，Cauchy矩阵，Leslie矩阵，幂等矩阵，幂零矩阵，循环矩阵等。

4.1 正规变换与正规矩阵

关注的是对角化的问题

4.2 Hermite变换与Hermite矩阵

关注的是对称的问题

4.3投影变换与投影矩阵

拉格朗日乘子法增加空间维数，投影方法将高维问题降维为低维问题。

几种特殊矩阵之间的关系

 

4.4 谱分解的应用-主成分分析

第一步：降维

第二步：正交化

第三步：能量最大化

4.5 矩阵的奇异值分解（SVD）

SVD分解与特征值分解的区别

（1）基的数目不同，SVD用了两组不同的基（左奇异向量和右奇异向量），而特征值分解只用一组基（特征向量）

（2）基的性质不一样，SVD使用了正交基，而特征值分解所用的基未必正交

（3）适用的矩阵不一样，SVD适用于所有矩阵，而特征值分解只适用于特定的方阵

（4）应用范围不同，SVD趋于侧重包含矩阵自身及其逆的问题，而特征值则趋于侧重包含有迭代的问题（如矩阵的幂及矩阵指数函数）

总结：SVD深刻揭示了矩阵的结构，即矩阵的秩

 

第五章 范数（norm）及其应用

范数是向量到实数的一种映射（函数），对向量这个兼具大小与方向即数与形的数学对象，范数度量的是向量的大小，即向量数的一面。

5.1 向量范数

（范数的定义）设V是数域F上的线性空间，对任意向量,按照某种对应规则，都有一个非负实数与之对应，并且对任意及任意，,都满足下列三个性质：

（1）正定性：；当且仅当时，=0

（2）正齐性：

（3）三角不等式：

则称是向量的范数，并称定义了范数的线性空间V为赋范线性空间。

注：

（1）范数未必都可由内积导出。

（2）内积空间是特殊的赋范线性空间。

常见范数：

（1）1范：

（2）2范：

（3）p范：

（4）无穷范：

（5）椭圆范数：(注：椭圆范数是用二范的形式定义的，说明可以从已知范数构造新的范数)

（二维向量的几种范数的几何意义）

（常见的距离测度）

（1）欧氏距离：

（2）绝对值距离：

（3）切氏距离：

（4）闵氏距离：

（5）马氏距离：

马氏距离分析：这里的x，y是从整体中抽取的两个样本，如果x，y来自两个数据集，则将S改为互协方差矩阵C（而前面4个距离描述的都是两个向量之间的距离）

注意：

（1）尽管各种范数大小不同，但作为度量用的不同“尺子”，它们对外表现出明显的一致性，正所谓“内斗外和”，这种性质就是范数的等价性

（2）处理向量问题，例如向量序列敛散性问题，我们可以基于一种范数来建立理论，而使用另一种范数来进行计算。

总结：无意间发现了宝贝，这本书对于矩阵学习者来说，更确切的说，是对于矩阵进阶学习者来说，是很好的书。从本科的基础知识引入，配上生动的故事，将原本复杂的概念娓娓道来。强烈推荐！

雅克比的一句有趣的话：如果你父亲坚持要先认识世界上所有的姑娘，然后再跟其中一个结婚，那他就永远不会结婚，而你现在也就不会在这里。