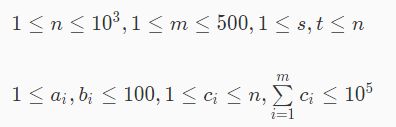链接:https://ac.nowcoder.com/acm/contest/5338/C
来源:牛客网
时间限制:C/C++ 1秒,其他语言2秒
空间限制:C/C++ 524288K,其他语言1048576K
64bit IO Format: %lld
空间限制:C/C++ 524288K,其他语言1048576K
64bit IO Format: %lld
题目描述
小雨所在的城市一共有
m 条地铁线,分别标号为 1 号线,2 号线,……,m 号线。整个城市一共有 n 个车站,编号为 1∼n 。其中坐 i 号线需要花费 ai 的价格,每坐一站就需要多花费 bi 的价格。
i 号线有 ci 个车站,而且这 ci 个车站都已知,如果某一站有多条地铁线经过,则可以在这一站换乘到另一条地铁线,并且能多次换乘。
现在小雨想从第 s 个车站坐地铁到第 t 个车站,地铁等待时间忽略不计,求最少花费的价格,若不能到达输出 -1 。(地铁是双向的,所以 s 可能大于 t)
输入描述:
第一行输入四个正整数 n,m,s,t,分别表示车站个数,地铁线数,起点站和终点站。
第二行到第 m+1 行,每行前三个数为 ai,bi,ci,分别表示坐 i 号线的价格,i 号线每坐一站多花的价格,i 号线车站个数。接下来 ci 个数,表示 i 号线的每一个车站的编号,单调递增。
输出描述:
共一行,一个数表示最小花费,若不能到达输出 -1 。
示例1
输入
5 2 1 4 2 2 3 1 3 5 2 1 4 2 3 4 5
输出
7
说明
坐 1 号线:花费 2;
1→3:花费 2;
换乘 2 号线:花费 2;
3→4:花费 1;
所以最小总花费为 7 。
备注:
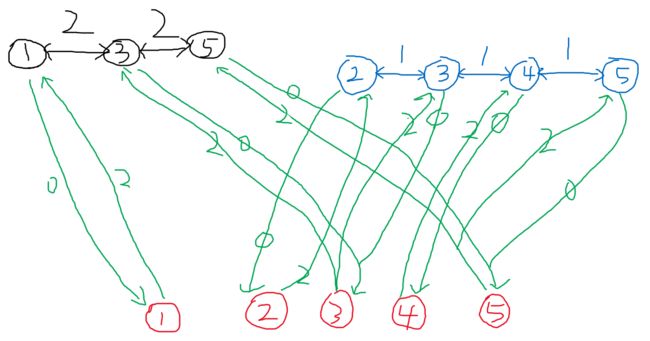
分层图最短路
每条地铁线看做是一层图,一共m层,,因为每层之间可能公用了一些节点,故第m+1层对每个车站都建立一个超级源点,这个超级源点连接每一层上和它编号相同的点
车站到超级源点的花费是0, 源点往车站的花费是坐该地铁的费用,最后跑一遍Dijkstra 找超级源点s到超级源点t的最短路
第i层第j号车站的编号就是(i-1)*n+j。因为取了m+1层,每层n个单位,所以最多有有(m+1) * n个不重复的编号。
从样例看:
从超级源点1 -> 1 -> 3 -> 超级源点3 -> 另一层线路的3 -> 4
总花费为 2 + 2 + 2 + 1 = 7
1 #include2 typedef long long LL; 3 #define pb push_back 4 const int INF = 0x3f3f3f3f; 5 const double eps = 1e-8; 6 const int mod = 1e9+7; 7 const int maxn = 1e6+10; 8 using namespace std; 9 10 int n,m,st,ed; 11 struct edge 12 { 13 int to; 14 int val; 15 int next; 16 }E[maxn];//注意边的条数 17 int head[maxn], tot; 18 void add(int u,int v,int val) 19 { 20 E[tot].to=v; 21 E[tot].val=val; 22 E[tot].next=head[u]; 23 head[u]=tot++; 24 } 25 26 int dis[maxn]; 27 void init() 28 { 29 tot=0; 30 memset(head,-1,sizeof(head)); 31 memset(dis,INF,sizeof(dis)); 32 } 33 struct cmp 34 { 35 bool operator()(int x,int y){ 36 return dis[x]>dis[y]; 37 } 38 }; 39 void Dijkstra(int st) 40 { 41 priority_queue<int,vector<int>,cmp > qe; 42 dis[st]=0; 43 qe.push(st); 44 while(!qe.empty()) 45 { 46 int u=qe.top(); qe.pop(); 47 for(int i=head[u];i!=-1;i=E[i].next) 48 { 49 int v=E[i].to; 50 if(dis[u]+E[i].val<dis[v]) 51 { 52 dis[v]=dis[u]+E[i].val; 53 qe.push(v); 54 } 55 } 56 } 57 } 58 59 int main() 60 { 61 #ifdef DEBUG 62 freopen("sample.txt","r",stdin); //freopen("data.out", "w", stdout); 63 #endif 64 65 scanf("%d %d %d %d",&n,&m,&st,&ed); 66 init(); 67 for(int i=1;i<=m;i++) 68 { 69 int num,a,b; 70 scanf("%d %d %d",&a,&b,&num); 71 int last = -1; 72 for(int j=1;j<=num;j++) 73 { 74 int x; 75 scanf("%d",&x); 76 if(last!=-1) 77 { 78 add((i-1)*n+x, (i-1)*n+last, b); 79 add((i-1)*n+last, (i-1)*n+x, b); 80 } 81 add((i-1)*n+x, m*n+x, 0);//连接这一层的这个号码到它的源点 82 add(m*n+x, (i-1)*n+x, a);//连接这个号码的源点到这一层的它 83 last = x; 84 } 85 } 86 Dijkstra(m*n+st); 87 printf(dis[m*n+ed]==INF?"-1\n":"%d\n",dis[m*n+ed]); 88 89 return 0; 90 }
-