最直白的编译原理-词法分析（清华-王书3版）

欢迎进入乱码IT的精神世界，请多指教~

词法分析

• 词法分析是编译过程的一个阶段：从左到右逐个字符的读入源程序，并对源程序字符流进行扫描和分解，识别出一个个单词。（对源程序的结构进行分析）

• PL/0编译程序将词法分析器作为子程序来调用，以语法分析器为主，语法分析器工作，需要词法分析器的输出作为输入，语法分析器需要分析时，发出请求调用词法分析器，词法分析器以二元式形式输出分析得到的单词符号，然后输入到语法分析器作为回应。（词法分析与语法分析在同一遍里，省掉了中间文件或储存区）

• 单词符号一般分类：
  1.关键字（例：If、while）
  2.标识符（例：常量名、变量名）
  3.常数（例、25、3.14、TRUE、ABC）
  4.运算符（例：+ - ）
  5.界符（例：逗号、括号）

• 二元式表示单词符号：（单词种别，单词自身的值）<例：（3，‘while’），‘3’表示单词种别为‘关键字’，该单词种别的值为‘while’>

• 词法分析器其他任务： 滤掉空格和注释、将行号与错误信息关联编译定位、完成编译预处理等

• 词法规则描述工具（即单词描述工具，分为两类：形式化、半形式化）：状态转换图、有穷自动机、正则表达式、正则文法等

正则文法与正则表达式的等价性

即两者之间的相互转换

转换规则如下：

例：

Z

有穷自动机FA

分两类：

• 不确定的有穷自动机NFA
• 确定的有穷自动机DFA

FA的表示（五元式）：
（状态结点集，输入符号表，转换函数，初态集，终态集）

注：

• 转换函数反映的是‘状态结点+输入符号→下一状态结点’的一种映射关系（f（k_i，a）=k_j ，（k∈K））
• 初态集：初态开始结点，如果是DFA则初态仅唯一一个

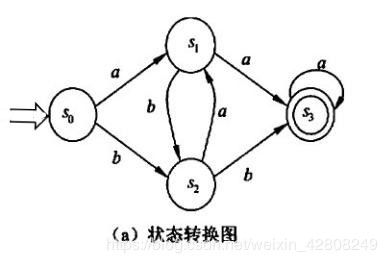
FA的状态图表示

注：

• 初态为箭头指向结点：‘→○’
• 终态为双圈结点：‘◎’

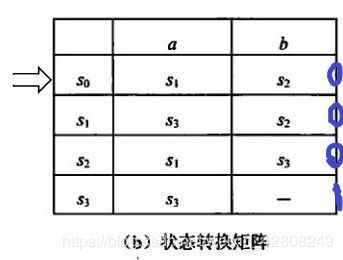
FA的矩阵表示

注：

• 第一列：所有状态结点
• 表头第一行：所有输入字符
• 若表格最左竖直边线外没有用箭头‘→’指示初态，则默认初态为第一个结点
• 表格最右竖直边线外，用‘0’表示非终态，‘1’表示终态

NFA确定化

即：将NFA装换为等价的DFA
方法：子集构造法

步骤：

1. 确定初态集：初态结点+初态结点出发输入‘ε’能连续到达的所有结点
2. 作输入到达关系表：第一列为我们构造的各个子集，表头第一行是所有输入符号（除了ε）
   注：（规则）
   A. 从初态集开始，初态集逐个元素查看 原NFA输入到达关系 ，能到达下一结点的取下一状态结点入新集，附加：若有自循环，保留自循环状态结点入新集，若下一结点后还有输入ε能到达连接的后续结点，则该类后续所有空连接结点也取入新集
   B.得到的新集从左往右顺序移到第一列从上到下重新开始新一轮的检验，直到检验完所有新集，不再产生新集则结束
3. 根据填好的输入到达表，对第一列各个集合从上到下标号，用标号重构一下输入到达表
4. 根据最新的输入到达表画出对应的DFA即可，此时NFA确定化完成

例：

1. 初态集为：{0}
2. 得到新输入到达表：
3. 重构输入到达表：
4. 画出对应DFA：

DFA最小化

即：化简DFA
方法：分割法

步骤：

1. 将原DFA的所有状态结点按终态、非终态分成两类两个集合
2. 逐个集合对每个集合逐个元素按照输入到达关系，查看是否有到达其他集合的情况，若有，将所有到达其他集合的元素从原集合分割出来形成新集合（单元素的不用考虑，直接跳过）
3. 重复至不可再分割
4. 取每个最终集合最小值为最简DFA的状态结点，再根据最初输入到达关系（当到达的是被删结点时，归到被删结点同集合结点上），重构最简输入到达表
5. 根据该最终输入到达表画出对应DFA（原来为初态的仍为初态，原来为终态的仍为终态），则化简完成

例：`

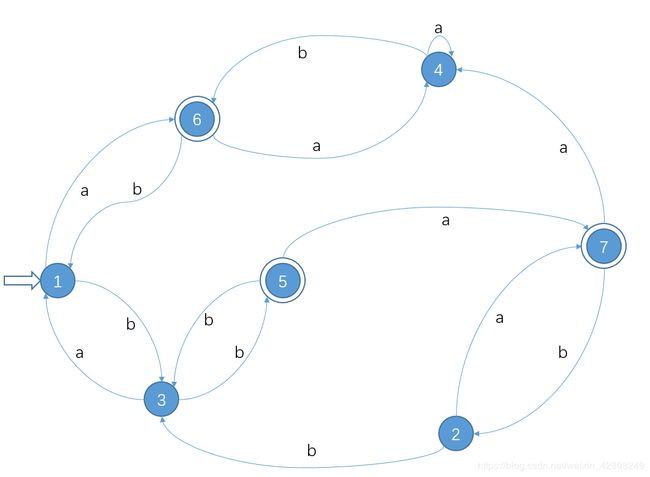
1.第一次分割：
非终态：I₀ = {1,2,3,4} ;
终态：I₁ = {5,6,7} ;

2.根据输入到达关系检验：
输入a时：

检验I₀= {1,2,3,4}： 1、2 到达了I₁= {5,6,7}

	将1、2从I0= {1,2,3,4}中分割出去： {1,2}，{3,4}，{5,6,7}

• 此时有：I₀ = {1,2} ，I₁ = {3,4} ，I₂ = {5,6,7}

再对I₂ = {5,6,7}检验输入a的到达情况：6、7到达了I₁= {3,4}

	将6、7从I2 = {5,6,7}中分割出去：{1,2}，{3,4}，{5}，{6,7}

• 此时有：I₀ = {1,2} ，I₁ = {3,4} ，I₂ = {5}，I₃ = {6,7}

再对I₀ = {1,2}检验输入a的到达情况：1、2都到达了I₃ = {6,7}，则不需要分割

再对I₁ = {3,4}检验输入a的到达情况：3到达了I₀ = {1,2}

	将3从I1 = {3,4}中分割出去：{1,2}，{3}，{4}，{5}，{6,7}

• 此时有：I₀ = {1,2} ，I₁ = {3} ，I₂ = {4}，I₃ = {5}，I₄ = {6,7}

跳过单元素的I₂ = {4}，I₃ = {5}，对I₄ = {6,7}检验输入a的到达情况：1、2都到达了I₂ = {4}，则不需要分割

输入b时：
重复检验输入a情况的方法，对输入b的情况进行分析

3.最终得： I₀ = {1,2} ，I₁ = {3} ，I₂ = {4}，I₃ = {5}，I₄ = {6,7}

4.{1} ， {3} ， {4}， {5}，{6}，重构输入到达表：

5.画出对应化简后的DFA：

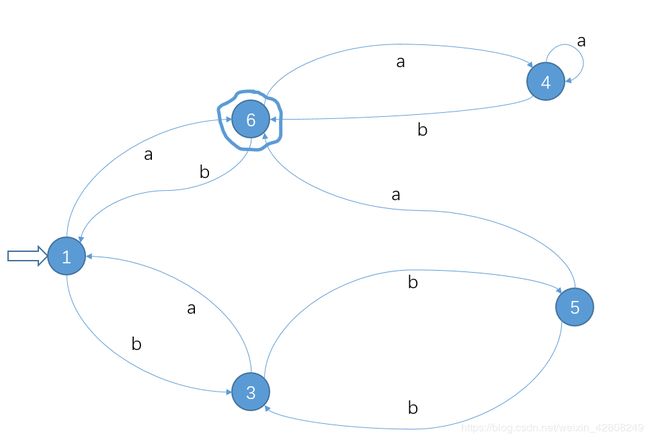
正规式与有穷自动机FA的等价性

即：正规式与FA的相互转换
转换规则（3条）：

1. 如下：

			 ‖

2.如下：

	                ‖

3.如下（ε连接和直接连接均可，注意自循环）：

或者

	            ‖

或者

1. 正规式→有穷自动机FA：
   步骤：

   1. 为正规式添上头和尾
      头：
      
      尾：
      
      2.根据实际情况拆分正规式并添加上结点
      3.不可拆时结束，完成转换

2. 有穷自动机FA→正规式：
   步骤：

   • 根据规则不断去除中间状态结点

（应用3条规则即可完成互相转换）

若对小主有用，求赞哟~

<也欢迎收藏，一起学习交流>