评分卡模型python实现

评分卡模型python实现

首先来介绍几个名词

• 变量分析：确定变量之间是否存在共线性，如存在高度相关，只保存最稳定、预测能力最高的那个。常用方法为VIF(variance inflation factor)，即方差膨胀因子进行检验。
• 变量分箱（binning）：是对连续变量离散化的称呼。常用的有等距分段、等深分段、最优分段。
• 单因子分析：检测各变量的强度，常用方法为：WOE、IV。

一、 实现步骤

1.对所有数据进行去极值以及缺失值处理；
2.数据拆分，将数据拆分成训练集、测试集；
3.对数据进行WOE离散化处理；
4.检验离散后的数据是否相关，从而决定是否进行降维处理；
5.调整训练集的平衡性；
6.训练模型，并使用测试集调整模型参数；
7.将通过验证后模型的权重提取出来，计算测试样本中每个客户的违约率；
8.用验证机验证模型的有效性及稳定性；
9.通过违约率给客户打分。

二、数据预处理

1. 加载数据以及去极值

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
# 1.载入数据
def load_data():
    data = pd.read_csv('/~~~/data.csv', sep=',')
    print(data.describe())
    return data
df_data = load_data()
# 2.多变量分析，相关性分析
import seaborn as sns
def corr(data):
    corr = data.corr()
    xticks = list(corr.index)
    yticks = list(corr.index)
    fig = plt.figure(figsize=(15, 10))
    ax1 = fig.add_subplot(1, 1, 1)
    sns.heatmap(corr, annot=True, cmap='rainbow', ax=ax1, linewidths=0.5,
                annot_kws={'size': 9, 'weight':'bold', 'color':'blue'})
    ax1.set_xticklabels(xticks, rotation=35, fontsize=15)
    ax1.set_yticklabels(yticks, rotation=0, fontsize=15)
    plt.show()
data = df_data.drop(['label'], axis =1)
corr(data)#一般剔除相关系数高于0.6的变量
# 3.去极值
'''
    xy=(横坐标，纵坐标)  箭头尖端
    xytext=(横坐标，纵坐标) 文字的坐标，指的是最左边的坐标
    arrowprops= {
        facecolor= '颜色',
        shrink = '数字' <1  收缩箭头
    }
'''
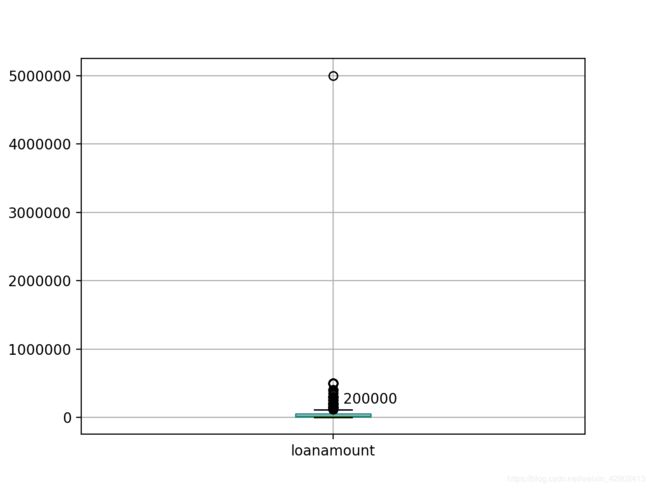
def outlier_check(data, cname):
    p = data[[cname]].boxplot(return_type='dict')
    print(p)
    x_outliers = p['fliers'][0].get_xdata()
    y_outliers = p['fliers'][0].get_ydata()
    for j in range(1):
        plt.annotate(y_outliers[j], xy=(x_outliers[j], y_outliers[j]),
                     xytext=(x_outliers[j] + 0.02, y_outliers[j]))
    plt.show()
#变量loanamount
outlier_check(df_data, 'loanamount')

删除1000000以上的：

df_data = df_data[df_data['loanamount']<1000000]

2.缺失值处理

       查看有无缺失值

def check_na(data):
    print(data.isnull().sum())
check_na(df_data)
#out:
risk             0
cycletime        0
loanamount       0
loanpurpose      0
seniority        0
monthlyincome    0
incometype       0

删除极值后，数据集无缺失值。
缺失值的具体处理方法可参考： https://blog.csdn.net/weixin_42902413/article/details/87856623

3.数据分箱

在Excel中计算各分箱的IV值，取IV最大的数据分箱。

3.1 WOE(Weight of Evidence)

       对分箱后的每组数据求woe。公式如下：
$$W_i=ln(\frac{p(y_i)}{p(n_i)})$$
       其中，$p(y_i)$表示当前条件下风险用户占总风险用户的比例，$p(n_i)$表示当前条件小无风险用户占无风险用户的比例。
       对上述公式变换后得到：
$$W_i=ln(\frac{p(y_i)}{p(n_i)})=ln(\frac{y_i/y_t}{n_i/n_t})=ln(\frac{y_i/ni}{y_t/n_t})$$
       WOE表示当前分组里风险用户和无风险用户的比值，和所有样本中风险用户和无风险用户的比值的差异。WOE越大，说明这种差异越大，这个分组里样本有风险的可能性就越大。

3.2 IV (information value)

       衡量某一个变量的信息量。
       计算公式为：
$$I{V}_i=(p(y_i)-p(n_i))\ast W_i,IV=\sum _{i=1}^n(I{V}_i)$$
IV值对应的预测能力

IV	预测能力
<0.03	无预测能力
0.03~0.09	低
0.1~0.29	中
0.3~0.49	高
>=0.5	极高

如果IV等于负或者正无穷时，都是没有意义的。针对某些风险比例为0或者100%的分组，建议做如下处理：

• 如果有可能，直接把这个分组作为一个规则，作为模型的前置条件或补充条件；
• 重新对变量进行离散化或分组，使每个组的风险比例不为0%且不为100%。（尤其当某个分组样本过少时，要采用这种方法）
• 如果上述两种方法都无用时，建议人工把该分组的风险数据和无风险数量进行一定的调整。（即0调成1，或1调成0）

       根据IV值来调整分箱结构并重新计算WOE和IV，知道IV达到最大值，此时的分箱效果最好。

# 数据分箱
# 1)自动分箱
def mono_bin(Y, X, n):
    r = 0
    badNum = Y.sum()
    goodNum = Y.count() - Y.sum()
    while abs(r) < 1:
        d1 = pd.DataFrame({'X': X, 'Y': Y, 'Bucket': pd.qcut(X, n)})
        d2 = d1.groupby('Bucket', as_index=True)
        # print('d1的类型是：', type(d1), 'd2的类型是：', type(d2))
        r, p = stats.spearmanr(d2.mean().X, d2.mean().Y)
        n = n-1
    d3 = pd.DataFrame()
    d3['min'] = d2.min().X
    d3['max'] = d2.max().X
    d3['badcostum'] = d2.sum().Y #坏样本的个数
    # print("badNum is :", badNum, "d3['badcostum'] is:", d3['badcostum'])
    d3['goodcostum'] = d2.count().Y - d2.sum().Y #好样本的个数
    d3['total'] = d2.count().Y
    d3['bad_rate'] = d2.sum().Y/d2.count().Y
    d3['woe'] = np.log(d3['badcostum']/d3['goodcostum']*(goodNum/badNum))
    iv = ((d3['badcostum']/badNum - d3['goodcostum']/goodNum)*d3['woe']).sum()
    d3['iv'] = iv
    woe = list(d3['woe'].round(6))
    cut = list(d3['max'].round(6))
    cut.insert(0, float('-inf'))
    cut[-1] = float('inf')
    return d3, iv, cut, woe

# # 2)手动分箱（离散变量）
def hand_bin(Y, X, cut):
    badNum = Y.sum()
    goodNum = Y.count() - Y.sum()
    d1 = pd.DataFrame({'X': X, 'Y': Y, 'Bucket':pd.cut(X, cut)})
    d2 = d1.groupby('Bucket', as_index=True)
    d3 = pd.DataFrame()
    d3['min'] = d2.min().X
    d3['max'] = d2.max().X
    d3['badcostum'] = d2.sum().Y
    d3['goodcostum'] = d2.count().Y - d2.sum().Y
    d3['total'] = d2.count().Y
    d3['bad_rate'] = d2.sum().Y/d2.count().Y
    # print('d3["bad_rate"] is:', d3['bad_rate'])
    d3['woe'] = np.log(d3['badcostum']/d3['goodcostum']*(goodNum/badNum))
    iv = ((d3['badcostum']/badNum - d3['goodcostum']/goodNum) * d3['woe']).sum()
    d3['iv'] = iv
    woe = list(d3['woe'].round(6))
    return d3, iv, cut, woe	
  
#对于不能自动分箱的特征，进行手动分箱，自定义cut
ninf = float('-inf')
pinf = float('inf')
cut1 = [ninf, 100, 200, 300, 500, pinf]
cut4 = [ninf, 100, 500, pinf]
cut5 = [ninf, 112, 182, pinf]
cut7 = [ninf, 1, 3, pinf]
cut8 = [ninf,  398, 1000, 5000, pinf]
cut9 = [ninf, 0, 60, 200, pinf]
cut11 = [ninf, 0, 1]

#数据分箱
dfx1, ivx1, cutx1, woex1 = hand_bin(df_data['survival'], df_data['certify_time'], cut1)
dfx2, ivx2, cutx2, woex2 = mono_bin(df_data['survival'], df_data['collect'], n=10)
dfx3, ivx3, cutx3, woex3 = mono_bin(df_data['survival'], df_data['collect_amount'], n=10)
dfx4, ivx4, cutx4, woex4 = hand_bin(df_data['survival'], df_data['collect_coupon_amount'], cut4)
dfx5, ivx5, cutx5, woex5 = hand_bin(df_data['survival'], df_data['least_collect'], cut5)
dfx6, ivx6, cutx6, woex6 = mono_bin(df_data['survival'], df_data['scan'], n=10)
dfx7, ivx7, cutx7, woex7 = hand_bin(df_data['survival'], df_data['pay'], cut7)
dfx8, ivx8, cutx8, woex8 = hand_bin(df_data['survival'], df_data['pay_amount'], cut8)
dfx9, ivx9, cutx9, woex9 = hand_bin(df_data['survival'], df_data['pay_coupon_amount'], cut9)
dfx10, ivx10, cutx10, woex10 = mono_bin(df_data['survival'], df_data['age'], n=10)
dfx11, ivx11, cutx11, woex11 = hand_bin(df_data['survival'], df_data['sex'], cut11)
# print('dfx1', dfx1, ivx1, cutx1, woex1)

4.woe替换

# woe替换
def  replace_woe(X, cut, woe):
    x_woe = pd.cut(X, cut, labels=woe)
    return x_woe
df_data['certify_time'] = Series(replace_woe(df_data['certify_time'], cutx1, woex1))
df_data['collect'] = Series(replace_woe(df_data['collect'], cutx2, woex2))
df_data['collect_amount'] = Series(replace_woe(df_data['collect_amount'], cutx3, woex3))
df_data['collect_coupon_amount'] = Series(replace_woe(df_data['collect_coupon_amount'], cutx4, woex4))
df_data['least_collect'] = Series(replace_woe(df_data['least_collect'], cutx5, woex5))
df_data['scan'] = Series(replace_woe(df_data['scan'], cutx6, woex6))
df_data['pay'] = Series(replace_woe(df_data['pay'], cutx7, woex7))
df_data['pay_amount'] = Series(replace_woe(df_data['pay_amount'], cutx8, woex8))
df_data['pay_coupon_amount'] = Series(replace_woe(df_data['pay_coupon_amount'], cutx9, woex9))
df_data['age'] = Series(replace_woe(df_data['age'], cutx10, woex10))
df_data['sex'] = Series(replace_woe(df_data['sex'], cutx11, woex11))
iv = [ivx1, ivx2, ivx3, ivx4, ivx5, ivx6, ivx7, ivx8, ivx9, ivx10, ivx11]
# print('iv is :', iv)
#去除IV值较小的两列
df_data = df_data.drop(['age', 'sex'], axis=1)
cut = [cutx1, cutx2, cutx3, cutx4, cutx5, cutx6, cutx7, cutx8, cutx9]
woe = [woex1, woex2, woex3, woex4, woex5, woex6, woex7, woex8, woex9]

5.数据拆分

       拆分成训练集和测试集

# 拆分数据，测试集、训练集
from random import sample
def data_sample(inputX, index, test_Ratio=0.2):
    data_array = np.atleast_1d(inputX) #将给定的所有数组，output的arrays中的所有array的维数均大于等于1
    class_array = np.unique(data_array)
    test_list = []
    train_list = []
    for c in class_array:
        temp = []
        for i, value in enumerate(data_array):
            if value == c:
                temp.append(index[i])
        test_list.extend(sample(temp, int(len(temp)*test_Ratio)))
    return list(set(index) - set(test_list)), test_list
def split_sample(data):
    train_list, test_list = data_sample(data['risk'].tolist(), data.index.tolist())
    df_train_section = data.ix[train_list, :]
    df_test_section = data.ix[test_list, :]
    return df_train_section, df_test_section

df_train, df_test = split_sample(df_data)
print(len(df_train), len(df_test)) # 8000 1999

6.数据标准化和SMOTE调整平衡性

       （1）数据标准化之前先将属性和标签拆分开，再对属性进行标准化：

# 1.df_train,训练集
Y_train = df_train['risk'].values.tolist()
X_train = df_train.drop(['risk'], axis=1)
std_series = X_train.std()
mean_series = X_train.mean()
X_train = X_train.add(mean_series).div(std_series)

# 2.df_test，测试集
Y_test = df_test['risk'].values.tolist()
X_test = df_test.drop(['risk'], axis=1)
std_series = X_test.std()
mean_series = X_test.mean()
X_test = X_test.add(mean_series).div(std_series)

       （2）由于风险用户占比较少，数据存在不平衡性。而逻辑回归模型倾向于自动删除高风险的用户，因此采用SMOTE法过采样违约用户，使得训练样本尽量平衡。

from collections import Counter
print(Counter(Y_train)) # 计算训练集中0和1的比例
from imblearn.over_sampling import SMOTE
smo = SMOTE(ratio={1: 4000}, random_state=42, n_jobs=1)
X_train, Y_train = smo.fit_sample(X_train, Y_train)
print(Counter(Y_train))

三、逻辑回归模型

1. 训练模型

       首先，为了确保数据进模型之前已经标准化，由于前面步骤已经标准化过了，接下来直接引入逻辑回归模型，并使用L2正则化防止过拟合。
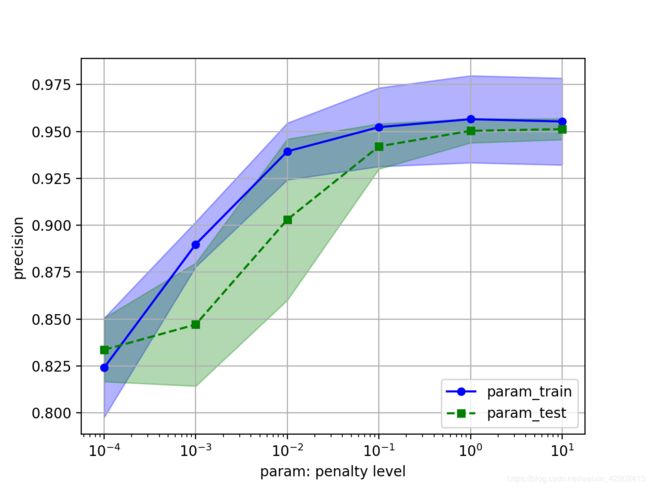
       其中正则化强度C由验证曲线validation_curve来确定，具体代码如下：

from sklearn.model_selection import validation_curve
from sklearn.linear_model import LogisticRegression
param_range = [0.001, 0.01, 0.1, 1, 10]
# 使用逻辑回归的验证器，验证的参数是C，3折交叉验证
train_scores, test_scores = validation_curve(estimator=LogisticRegression(dual=True),
                                           X=X_train, y=Y_train, param_name='C', param_range=param_range, cv=3)
train_mean = np.mean(train_scores, axis=1)
train_std = np.std(train_scores, axis=1)
test_mean = np.mean(test_scores, axis=1)
test_std = np.std(test_scores, axis=1)
plt.plot(param_range, train_mean, color='b', marker='o', markersize=5, label='param_train')
plt.fill_between(param_range, train_mean+train_std, train_mean-train_std, alpha=0.3, color='b')
plt.plot(param_range, test_mean, ls='--', color='g', marker='s', markersize=5, label='param_test')
plt.fill_between(param_range, test_mean+test_std, test_mean-test_std, alpha=0.3, color='g')
plt.grid()
plt.xscale('log')
plt.xlabel('param: penalty level')
plt.ylabel('precision')
plt.legend(loc='lower right')
plt.show()

验证曲线如下：（取C=0.1）

2. 计算权重

# 得出权重
from sklearn.linear_model import LogisticRegression
LR = LogisticRegression(dual=True, C=1)
LR.fit(X_train, Y_train)
weight = LR.coef_[0]
intercept = LR.intercept_[0]
coe = list(weight)
coe.append(intercept)

四、模型验证

1.测试集验证

测试集精度：

from sklearn import metrics
y_pred = LR.predict(X_test)
print(metrics.confusion_matrix(Y_test, y_pred))#输出混淆矩阵

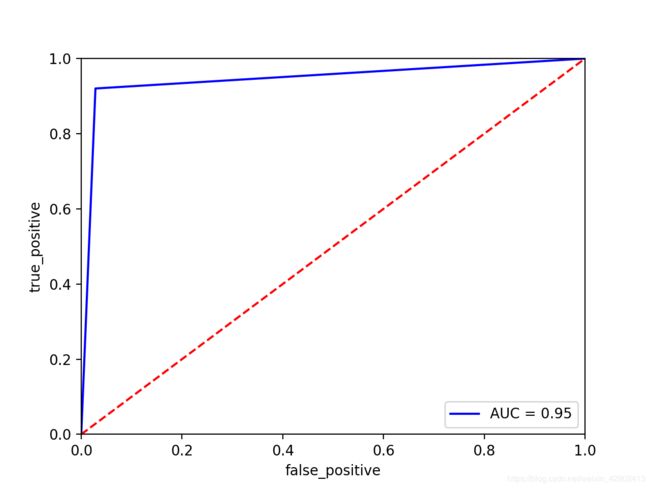
2. ROC曲线

from sklearn import metrics
fpr, tpr, threshold = metrics.roc_curve(Y_test, y_pred)
rocauc = metrics.auc(fpr, tpr)
plt.plot(fpr, tpr, 'b', label='AUC = %0.2f' % rocauc)
plt.legend(loc='lower right')
plt.plot([0, 1], [0, 1], 'r--')
plt.xlim([0, 1])
plt.ylim([0, 1])
plt.ylabel('true_positive')
plt.xlabel('false_positive')
plt.show()

ROC曲线如下：

五.信用评分

个人总评分 = 基础分+各部分得分

1.基础分

基础分值定为600分，PDO(比率翻倍的分值)好坏比定为20.

import math
p = 20/math.log(2)
q = 600 - 20 * math.log(20)/math.log(1)
baseScore = round(q + p * coe[0], 0)

2.各部分评分

def get_score(coe, woe, factor):
    # print('coe, woe, factor are:', coe, woe, factor)
    scores = []
    for w in woe:
        score = round(coe * w * factor, 0)
        scores.append(score)
    return scores
x1 = get_score(coe[0], woe[0], p)
x2 = get_score(coe[1], woe[1], p)
x3 = get_score(coe[2], woe[2], p)
x4 = get_score(coe[3], woe[3], p)
x5 = get_score(coe[4], woe[4], p)
x6 = get_score(coe[5], woe[5], p)
x7 = get_score(coe[6], woe[6], p)
x8 = get_score(coe[7], woe[7], p)
x9 = get_score(coe[8], woe[8], p)
score = [x1, x2, x3, x4, x5, x6, x7, x8, x9]

3.自动评分

       因为是先分箱再进行数据切分的，对测试集也进行了woe值替换，所以要用woe值进行对比；如果先进行数据切分，不对测试集进行woe值替换，则用cut值进行比较
       1）定义函数

#定义评分计算函数
def compute_score(series, woe, score):
    list = []
    # print('series.iloc[1]={}'.format(series.iloc[1]))
    print('woe={}'.format(woe))
    print('score={}'.format(score))
    for i in range(len(series)):
        value = series.iloc[i]
        print('value={}'.format(value))
        s = []
        for j in range(len(woe)):
            if value == woe[j]:
                print('woe={}'.format(woe))
                s = score[j]
                print('s = {}'.format(s))
                # ss.append(s)
        list.append(s)
    # print('list={}'.format(list))
    # list = pd.Series(list)
    # print('list={}'.format(list))
    return list

       2）计算各测试集的分值

# 计算
df_test['x1'] = compute_score(df_test['certify_time'], woe[0], x1)
#print(df_test['x1'])
#print(pd.DataFrame({"certify_time": df_test['certify_time'], 'x1': df_test['x1']}))
df_test['x2'] = compute_score(df_test['collect'], woe[1], x2)
df_test['x3'] = compute_score(df_test['collect_amount'], woe[2], x3)
df_test['x4'] = compute_score(df_test['collect_coupon_amount'], woe[3], x4)
df_test['x5'] = compute_score(df_test['least_collect'], woe[4], x5)
df_test['x6'] = compute_score(df_test['scan'], woe[5], x6)
df_test['x7'] = compute_score(df_test['pay'], woe[6], x7)
df_test['x8'] = compute_score(df_test['pay_amount'], woe[7], x8)
df_test['x9'] = compute_score(df_test['pay_coupon_amount'], woe[8], x9)
df_test['score'] = baseScore + df_test['x1'] + df_test['x2'] + df_test['x3'] + df_test['x4'] + df_test['x5'] + df_test['x6'] + df_test['x7'] + df_test['x8'] + df_test['x9']
# print(df_test['x1'].head())
print(df_test['score'].head())

输出结果：

id      score
2797    432.0
4480    430.0
7864    401.0
8418    393.0
9077    401.0

        至此，第一次评分卡流程走完了，当然还有很多可以优化的地方。后面也许会更新另一个实际项目，加油！