DBSCAN聚类原理及详解
DBSCAN聚类
(1)DBSCAN简介
DBSCAN是一个比较有代表性的基于密度的聚类算法。与划分和层次聚类方法不同,它将簇定义为密度相连的点的最大集合,能够把具有足够高密度的区域划分为簇,并可在噪声的空间数据库中发现任意形状的聚类。
DBSCAN中的几个定义:
Ε邻域:给定对象半径为Ε内的区域称为该对象的Ε邻域;
核心对象:如果给定对象Ε邻域内的样本点数大于等于min_samples,则称该对象为核心对象;
直接密度可达:对于样本集合D,如果样本点q在p的Ε邻域内,并且p为核心对象,那么对象q从对象p直接密度可达。
密度可达:对于样本集合D,给定一串样本点p1,p2….pn,p= p1,q= pn,假如对象pi从pi-1直接密度可达,那么对象q从对象p密度可达。
密度相连:存在样本集合D中的一点o,如果对象o到对象p和对象q都是密度可达的,那么p和q密度相联。
DBSCAN中两个重要参数eps ,min_samples
(1)eps:越大类别数越少——参数越大的话,多个簇和大部分对象会归并到同一个簇中
(2)需要对eps和min_samples手动设置,eps默认值是0.5,表示的是半径
如果 附近点的数量 ≥min_samples,则当前点与其附近点形成一个簇,并且出发点被标记为已访问(visited),如果 附近点的数量
(4)min_samples的选取有一个指导性的原则(a rule of thumb),min_samples ≥dim+1,其中dim表示待聚类数据的维度。min_samples设置为1是不合理的,因为设置为1,则每个独立点都是一个簇,min_samples≤2时,与层次距离最近邻域结果相同,因此,min_samples必须选择大于等于3的值。若该值选取过小,则稀疏簇中结果由于密度小于min_samples,从而被认为是边界点儿不被用于在类的进一步扩展;若该值过大,则密度较大的两个邻近簇可能被合并为同一簇。因此,该值是否设置适当会对聚类结果造成较大影响,如果min_samples不变,Eps取得值过大,会导致大多数点都聚到同一个簇中,Eps过小,会导致一个簇的分裂;如果Eps不变,min_samples的值取得过大,会导致同一个簇中点被标记为离群点,min_samples过小,会导致发现大量的核心点。
(2)实现步骤
导入使用的模块和库
将样本点设为1000个, 参数设置为noise=0.1,用datasets.make_blobs函数生成样本点1000个, 参数设置为n_features=2, centers=[[1.2,1.2]], cluster_std=0.1,random_state设为学号除以30取余数
展示出原始数据如下所示
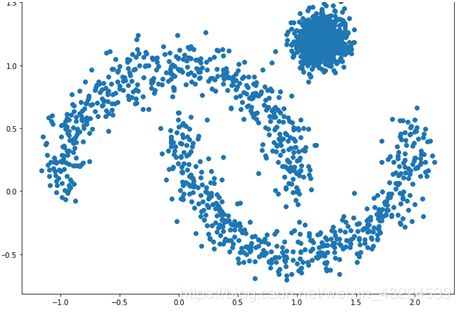
先用kmeans实现聚类,看看聚类效果

用kmeans进行聚类,聚类效果如下,聚成了3类
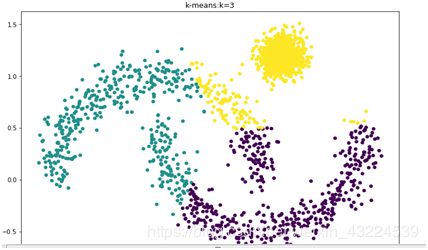
Silhouette Coefficient: 0.626(轮廓系数)
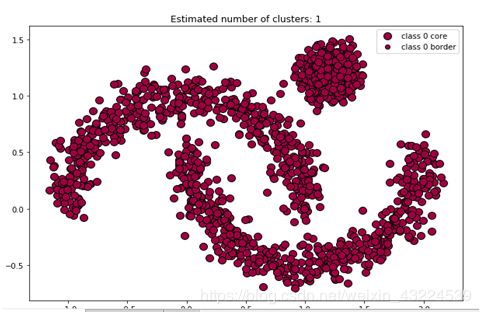
然后用DBSCAN聚类,先使用默认参数,观察聚类效果(默认参数eps=0.5 min_samples=5)

然后将参数eps改为0.1,看一下聚类效果

将EPS=0.1改为0.1,领域减小,类别增多,聚成了3类,聚类结果如下
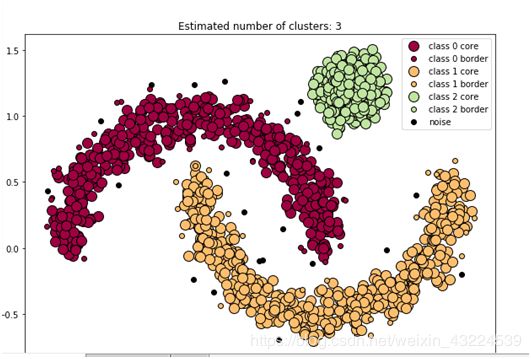
将参数eps改为0.1,min_samples改为15,聚类效果如下

(3)总结
优点
- 与K-means方法相比,DBSCAN不需要事先知道要形成的簇类的数量。
- 与K-means方法相比,DBSCAN可以发现任意形状的簇类。
- 同时,DBSCAN能够识别出噪声点。
- DBSCAN对于数据库中样本的顺序不敏感,即Pattern的输入顺序对结果的影响不大。但是,对于处于簇类之间边界样本,可能会根据哪个簇类优先被探测到而其归属有所摆动。
缺点
(1) DBSCAN不能很好反映高维数据。
(2)DBSCAN不能很好反映数据集以变化的密度。
(3)如果样本集的密度不均匀、聚类间距差相差很大时,聚类质量较差。
(4)源代码展示
import numpy as np
import matplotlib.pyplot as plt
from sklearn import metrics
from sklearn import datasets
from sklearn.cluster import DBSCAN
#%% 生成、展示数据
X1,y1=datasets.make_moons(n_samples=1000,noise=0.1,random_state=16050416121%30)#生成两组数据
X2, y2 = datasets.make_blobs(n_samples=1000, n_features=2, centers=[[1.2,1.2]],#y1y2是标签
cluster_std=[[0.1]], random_state=16050416121%30)
X = np.concatenate((X1, X2)) #纵向拼接
plt.figure(figsize=(10, 7))
plt.title('original data')
plt.plot(X[:, 0], X[:, 1], 'o',markersize=6)
plt.show()
#%% 首先看看K-Means的聚类效果
from sklearn.cluster import KMeans
y_pred = KMeans(n_clusters=3, random_state=9).fit_predict(X)#对x预测
plt.figure(figsize=(10, 7))
plt.scatter(X[:, 0], X[:, 1],s=25, c=y_pred)#颜色
plt.title('k-means:k=3')
plt.show()
print("Silhouette Coefficient: %0.3f"
% metrics.silhouette_score(X, y_pred))
#%% 那么如果使用DBSCAN效果如何呢?我们先不调参,直接用默认参数,看看聚类效果,:
db = DBSCAN().fit(X) #用DBSCAN拟合 #0.5 5
core_samples_mask = np.zeros_like(db.labels_, dtype=bool)#核心样本点 创建一个已知维度的数组,用0填充
core_samples_mask[db.core_sample_indices_] = True #将核心点赋值为true
labels = db.labels_
n_clusters_ = len(set(labels)) - (1 if -1 in labels else 0) #
unique_labels = set(labels) #去掉重复的元素
colors = [plt.cm.Spectral(each)
for each in np.linspace(0, 1, len(unique_labels))]
# 1)np.linspace 返回[0,1]之间的len(unique_labels) 个数
# 2)plt.cm 一个颜色映射模块
# 3)生成的每个colors包含4个值,分别是RGBA:
# RGBA是代表Red(红色) Green(绿色) Blue(蓝色)和 Alpha的色彩空间,
# 也就是透明度/不透明度
# 4)其实这行代码的意思就是生成len(unique_labels)个可以和光谱对应的颜色值
plt.figure(figsize=(10, 7))
for k, col in zip(unique_labels, colors): #遍历
class_member_mask = (labels == k) #等于k是true
if k == -1: #被判定的噪声点
cls = 'noise'
xy = X[class_member_mask] #
plt.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor='k',
markeredgecolor='k', markersize=6,label=cls) #
else:
xy = X[class_member_mask & core_samples_mask] #核心点
plt.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=tuple(col),
markeredgecolor='k', markersize=10,label= 'class '+ str(k)+' core')
xy = X[class_member_mask & ~core_samples_mask] #边缘点
plt.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=tuple(col),
markeredgecolor='k', markersize=6,label= 'class '+ str(k)+' border')
plt.legend(loc='best')
plt.title('Estimated number of clusters: %d' % n_clusters_)
plt.show()
#%% 对DBSCAN的两个关键的参数eps和min_samples进行调参!发现,类别数太少,
#需要增加类别数,可以减少eps-邻域的大小,默认是0.5,减到0.1看看效果,min_samples默认5
db = DBSCAN(eps=0.1).fit(X) #0.1 5
core_samples_mask = np.zeros_like(db.labels_, dtype=bool)
core_samples_mask[db.core_sample_indices_] = True
labels = db.labels_
n_clusters_ = len(set(labels)) - (1 if -1 in labels else 0)
unique_labels = set(labels)
colors = [plt.cm.Spectral(each)
for each in np.linspace(0, 1, len(unique_labels))]
plt.figure(figsize=(10, 7))
for k, col in zip(unique_labels, colors):
class_member_mask = (labels == k)
if k == -1: #被判定的噪声点
cls = 'noise'
xy = X[class_member_mask]
plt.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor='k',
markeredgecolor='k', markersize=6,label=cls)
else:
xy = X[class_member_mask & core_samples_mask] #核心点
plt.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=tuple(col),
markeredgecolor='k', markersize=12,label='class '+ str(k)+' core')
xy = X[class_member_mask & ~core_samples_mask] #边缘点
plt.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=tuple(col),
markeredgecolor='k', markersize=6,label='class '+ str(k)+' border')
plt.legend(loc='best')
plt.title('Estimated number of clusters: %d' % n_clusters_)
plt.show()
#%% 对DBSCAN的两个关键的参数eps和min_samples进行调参!发现,类别数太少,
#需要增加类别数,可以增大min_samples值,增大到15,看看效果 0.1 15
y_pred = DBSCAN(eps = 0.1, min_samples = 15).fit_predict(X)
plt.figure(figsize=(10, 7))
plt.scatter(X[:, 0], X[:, 1],s=25, c=y_pred)
plt.title('Estimated number of cluster:%d' )
plt.title('DBSCAN:eps=0.1, min_samples=15')
plt.show()
print("Silhouette Coefficient: %0.3f"
% metrics.silhouette_score(X, y_pred))
#%% 对DBSCAN的两个关键的参数eps和min_samples进行调参!发现,类别数太少,
#需要增加类别数,可以增大min_samples值,增大到10,看看效果 0.1 10
y_pred = DBSCAN(eps = 0.1, min_samples = 10).fit_predict(X)
plt.figure(figsize=(10, 7))
plt.scatter(X[:, 0], X[:, 1],s=25, c=y_pred)
plt.title('Estimated number of cluster:%d' )
plt.title('DBSCAN:eps=0.1, min_samples=10')
plt.show()
print("Silhouette Coefficient: %0.3f"
% metrics.silhouette_score(X, y_pred))