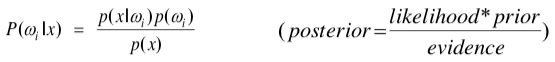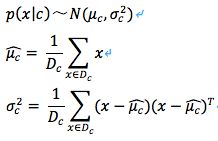机器学习之贝叶斯学习
机器学习之贝叶斯学习
一、概述
二、贝叶斯决策论
1. 什么是贝叶斯公式？
2. 最小错误率贝叶斯决策
3. 最小风险贝叶斯决策
4. 极大似然估计（MLE）
三、贝叶斯分类器
1. 朴素贝叶斯分类器基本知识
2. 三种常见的模型
2. 贝叶斯分类器的实际应用
四、总结
五、参考资料
一、概述
贝叶斯决策最大的特点就是依赖先验，通俗来说，就是根据之前的依据，对未来发生的可能性就行判断。
# Example1
Q：我们想知道怀柔区明天下不下雨？
A：可以根据过去10年来，怀柔区365（或366）天有多少天下雨，有多少天不下雨进行判断。再进一步来看，现在是冬季，可以根据过去10年，怀柔区冬季的降雨天数、怀柔区所处气候带等特征进行判断。
总结：要判断明天、明年等（属于后验概念）发生的可能性，需要根据之前的依据进行判断分析，就是依赖先验。
二、贝叶斯决策论
1. 什么是贝叶斯公式？
1）基于概率论的角度
2）基于观察特征、类别的贝叶斯公式
2. 最小错误率贝叶斯决策
1）样本错误率
2）整体错误率
若想得到最小错误率，正确率
必须达到最大，即
因此，最小错误率贝叶斯决策等价于最大后验概率决策。
3. 最小风险贝叶斯决策
4. 极大似然估计（MLE）
估计类条件概率的一种常用策略是先假定其具有某种确定的概率分布形式，在基于训练样本对概率分布的参数进行估计。
事实上，概率模型的训练过程就是参数估计的过程。
1）假设这些样本独立分布
2）当这些样本为连续属性时
三、贝叶斯分类器
1. 朴素贝叶斯分类器基本知识
前提条件：对已知类别，假设所有属性相互独立
4）朴素贝叶斯的优缺点
- 优点：学习和预测的效率高，且易j于实现。当训练数据较少时，也可以通过极大似然估计估计出必要的的参数。
- 缺点：分类效果不一定很高。特征独立性使得朴素贝叶斯变得简单，但是会牺牲一定的分类准确率。
2. 三种常见的模型
1）高斯模型
当要处理的为连续数据时（如人的身高、物体长度等），我们都可以将其转化成离散型的值。比如身高160cm以下，特征值为1；身高160cm-180cm之间，特征值为2；身高180cm+，特征值为3。不过这些方式得出的值都不够细腻，使用朴素贝叶斯分类器中的高斯模型可以解决连续型数值问题。高斯模型假设每一维特征都服从高斯分布，即正态分布。
# Experiment 1 下面将用sklearn函数库中的Iris数据集进行实验
实验结果：
由上述结果来看，预测结果准确。
2）多项式模型
当特征是离散的时候，常使用朴素贝叶斯中的多项式模型。从朴素贝叶斯基础知识来看，当训练集不足时，可能导致先验概率和条件概率为0，因此会进行平滑处理。多项式模型公式为：
# Experiment 2 下面将用sklearn函数库进行实验
实验结果：
由上述结果来看，预测结果准确
3）伯努利模型
与多项式模型一样，伯努利模型只允许使用离散的特征。但是，伯努利模型每个特征的取值是布尔型：True or False，或者0和1。在伯努利模型中，条件概率的计算公式：
# Experiment 3 下面用sklearn函数库进行实验
实验结果：
由上述结果来看，预测结果准确
2. 贝叶斯分类器的实际应用
1）文本分类
前提是假设各文本之间相互独立，不考虑上下文、语境分析等。
- 在多项式模型中
- 在伯努利模型中
# Example 2 垃圾邮件内容识别
Q：假设我们有垃圾邮件和正常内容邮件各1万封，如何判断以下这封邮件是否是垃圾邮件？
邮件内容：“我司可办理正规发票（保真）17%增值税发票点数优惠！”
A：
1. 我们选择使用朴素贝叶斯分类器。
目标就是判断p(“垃圾邮件”|“某特征”)是否大于1/2。用Example2来看，就是判断p(“垃圾邮件”|“我司可办理正规发票（保真）17%增值税发票点数优惠！”)是否大于1/2。
然而，大多数垃圾邮件都不会出现完全相同的句子，如果加一些标点，修改文字或数字等，算出来的概率会失真，就不能检测出该内容是否属于垃圾邮件。
2. NLP的最重要技术之一— 分词
句子的可能性是无限的，但是属于垃圾邮件的词语却是有限的！
运用现在较好的中文分词工具---结巴分词
将邮件内容拆分成以下单词：“我”，“司”，“可”，“办理”，“正规”，“发票”，“保真”，“增值税”，“发票”，“点数”，“优惠”
因此，公式变为
- p(“垃圾邮件”|(“我”，“司”，“可”，“办理”，“正规”，“发票”，“保真”，“增值税”，“发票”，“点数”，“优惠”))
=p((“我”，“司”，“可”，“办理”，“正规”，“发票”，“保真”，“增值税”，“发票”，“点数”，“优惠”)| “垃圾邮件”)*P(“垃圾邮件”)
/P((“我”，“司”，“可”，“办理”，“正规”，“发票”，“保真”，“增值税”，“发票”，“点数”，“优惠”))
- p(“正常邮件”|(“我”，“司”，“可”，“办理”，“正规”，“发票”，“保真”，“增值税”，“发票”，“点数”，“优惠”))
=p((“我”，“司”，“可”，“办理”，“正规”，“发票”，“保真”，“增值税”，“发票”，“点数”，“优惠”)| “正常邮件”)*P(“正常邮件”)
/P((“我”，“司”，“可”，“办理”，“正规”，“发票”，“保真”，“增值税”，“发票”，“点数”，“优惠”))
3. 应用朴素贝叶斯分类器
朴素贝叶斯的前提是假设各属性独立分布，令S表示“垃圾邮件”，“H”表示“正常邮件”。
p((“我”，“司”，“可”，“办理”，“正规”，“发票”，“保真”，“增值税”，“发票”，“点数”，“优惠”)| S)
= p(“我”|S) * p(“司”|S) * p(“可”|S) * p(“办理”|S) * p(“正规”|S) * p(“发票”|S) * p(“保真”|S) * p(“增值税”|S) * p(“发票”|S) * p(“点数”|S) * p(“优惠”|S)
p((“我”，“司”，“可”，“办理”，“正规”，“发票”，“保真”，“增值税”，“发票”，“点数”，“优惠”)| H)
= p(“我”|H) * p(“司”|H) * p(“可”|H) * p(“办理”|H) * p(“正规”|H) * p(“发票”|H) * p(“保真”|H) * p(“增值税”|H) * p(“发票”|H) * p(“点数”|H) * p(“优惠”|H)
因此，我们只需比较
C1 = p(“我”|S) * p(“司”|S) * p(“可”|S) * p(“办理”|S) * p(“正规”|S) * p(“发票”|S) * p(“保真”|S) * p(“增值税”|S) * p(“发票”|S) * p(“点数”|S) * p(“优惠”|S) * p(S)
C2 = p(“我”|H) * p(“司”|H) * p(“可”|H) * p(“办理”|H) * p(“正规”|H) * p(“发票”|H) * p(“保真”|H) * p(“增值税”|H) * p(“发票”|H) * p(“点数”|H) * p(“优惠”|H) * p(H)
要计算C1和C2，只需统计每个词在垃圾邮件/正常邮件中出现的概率即可。当样本数量足够时，算出来的概率还是很高的，基本可以实现垃圾邮件的识别分类。
4. 多项式模型和伯努利模型
仔细看C1式，p(“发票”|S)出现了两次，由1.2.2总结的多项式模型知识，可知，C1计算出来的是多项式模型下的概率。
另一种简化的方法是采用伯努利模型，即将重复出现的词语视为只出现了1次。因为它丢失了部分词频，所以效果会比使用多项式模型略差一些。
在计算时，同样遵循平滑处理的原则，避免出现失真现象。
四、总结
- 贝叶斯学习主要是基于贝叶斯公式进行变换、学习。
- 贝叶斯学习中一个著名的分类器---朴素贝叶斯分类器。朴素贝叶斯分类器有一个前提条件，就是假设所有属性相互独立。
- 朴素贝叶斯中有3个著名模型，分别是高斯模型、多项式模型和伯努利模型。高斯模型允许特征为连续值，多项式模型和伯努利模型只允许离散型特征。
- 贝叶斯学习是基于统计方法的，在自然语言处理中对于文本分类等具有很好的效果，但是，朴素贝叶斯分类器不考虑词语之间的顺序关系，如：“武松打死了老虎”和“老虎打死了武松”，运用朴素贝叶斯分类器来计算是无区别的，使用N-Gram等模型可以提高文本分类的准确率。
五、参考资料
[1]《贝叶斯机器学习前沿进展综述》
[2] 《机器学习》--- 周志华
[3] 贝叶斯理论及3种常见模型https://blog.csdn.net/u012162613/article/details/48323777
- 代码，包括常见的其他算法https://github.com/wepe/MachineLearning
[4] Bayes Methods for Hackershttps://github.com/CamDavidsonPilon/Probabilistic-Programming-and-Bayesian-Methods-for-Hackers
[5] Naive Bayes Spam Filteringhttps://en.wikipedia.org/wiki/Naive_Bayes_spam_filtering