机器学习十大经典算法之岭回归和LASSO回归(学习笔记整理)
在线性回归模型中,其参数估计公式为 β = ( X T X ) − 1 X T y \beta=(X^TX)^{-1}X^Ty β=(XTX)−1XTy,当 X T X X^TX XTX不可逆时无法求出 β \beta β,另外如果 ∣ X T X ∣ |X^TX| ∣XTX∣越趋近于0,会使得回归系数趋向于无穷大,此时得到的回归系数是无意义的。解决这类问题可以使用岭回归和LASSO回归,主要针对自变量之间存在多重共线性或者自变量个数多于样本量的情况。
一、岭回归
1.参数推导
线性回归模型的目标函数 J ( β ) = ∑ ( y − X β ) 2 J(\beta)=\sum(y-X\beta)^2 J(β)=∑(y−Xβ)2
为了保证回归系数 β \beta β可求,岭回归模型在目标函数上加了一个L2范数的惩罚项 J ( β ) = ∑ ( y − X β ) 2 + λ ∣ ∣ β ∣ ∣ 2 2 = ∑ ( y − X β ) 2 + ∑ λ β 2 J(\beta)=\sum(y-X\beta)^2+\lambda||\beta||^2_2\\\text {}\qquad\;\;=\sum(y-X\beta)^2+\sum\lambda\beta^2 J(β)=∑(y−Xβ)2+λ∣∣β∣∣22=∑(y−Xβ)2+∑λβ2其中 λ \lambda λ为非负数, λ \lambda λ越大,则为了使 J ( β ) J(\beta) J(β)最小,回归系数 β \beta β就越小。
推导过程:
J ( β ) = ( y − X β ) T ( y − X β ) + λ β T β = y T y − y T X β − β T X T y + β T X T X β + λ β T β J(\beta)=(y-X\beta)^T(y-X\beta)+\lambda\beta^T\beta\\\text{}=y^Ty-y^TX\beta-\beta^TX^Ty+ \beta^TX^TX\beta+\lambda\beta^T\beta J(β)=(y−Xβ)T(y−Xβ)+λβTβ=yTy−yTXβ−βTXTy+βTXTXβ+λβTβ 令 ∂ J ( β ) ∂ β = 0 令\frac{\partial J(\beta)}{\partial \beta}=0 令∂β∂J(β)=0 ⇒ 0 − X T y − X T y + 2 X T X β + 2 λ β = 0 \Rightarrow0-X^Ty-X^Ty+2X^TX\beta+2\lambda\beta=0 ⇒0−XTy−XTy+2XTXβ+2λβ=0 ⇒ β = ( X T X + λ I ) − 1 X T y \Rightarrow\beta=(X^TX+\lambda I)^{-1}X^Ty ⇒β=(XTX+λI)−1XTyL2范数惩罚项的加入使得 ( X T X + λ I ) (X^TX+\lambda I) (XTX+λI)满秩,保证了可逆,但是也由于惩罚项的加入,使得回归系数 β \beta β的估计不再是无偏估计。所以岭回归是以放弃无偏性、降低精度为代价解决病态矩阵问题的回归方法。
单位矩阵 I I I的对角线上全是1,像一条山岭一样,这也是岭回归名称的由来。
2. λ \lambda λ的选择
- 模型的方差:回归系数的方差
- 模型的偏差:预测值和真实值的差异
随着模型复杂度的提升,在训练集上的效果就越好,即模型的偏差就越小;但是同时模型的方差就越大。对于岭回归的 λ \lambda λ而言,随着 λ \lambda λ的增大, ∣ X T X + λ I ∣ |X^TX+\lambda I| ∣XTX+λI∣就越大, ( X T X + λ I ) − 1 (X^TX+\lambda I)^{-1} (XTX+λI)−1就越小,模型的方差就越小;而 λ \lambda λ越大使得 β \beta β的估计值更加偏离真实值,模型的偏差就越大。所以岭回归的关键是找到一个合理的 λ \lambda λ值来平衡模型的方差和偏差。
根据凸优化,可以将岭回归模型的目标函数 J ( β ) J(\beta) J(β)最小化问题等价于
{ a r g m i n { ∑ ( y − X β 2 ) } ∑ β 2 ≤ t \begin{cases} argmin\{\sum(y-X\beta^2)\}\\[2ex]\sum\beta^2\leq t \end{cases} ⎩⎨⎧argmin{∑(y−Xβ2)}∑β2≤t
其中t为一个常数。以最简单的二维为例,即 β ( β 1 , β 2 ) \beta(\beta_1,\beta_2) β(β1,β2)其几何图形是


图片转自:https://www.jianshu.com/p/1677d27e08a7
抛物面代表的是 ∑ ( y − X β ) 2 \sum(y-X\beta)^2 ∑(y−Xβ)2的部分,圆柱体代表的是 β 1 2 + β 2 2 ≤ t \beta_1^2+\beta_2^2\leq t β12+β22≤t的部分。最小二乘解是抛物面的中心,岭回归解是抛物面与圆柱体的交点。岭回归的惩罚项 ∑ λ β 2 \sum\lambda\beta^2 ∑λβ2是关于回归系数 β \beta β的二次函数,对目标函数求偏导时会保留 β \beta β,抛物面与圆柱体很难相交于轴上使某个变量的回归系数为0,因此岭回归不能实现变量的剔除。
(1)岭迹法确定 λ \lambda λ值
由 β = ( X T X + λ I ) − 1 X T y \beta=(X^TX+\lambda I)^{-1}X^Ty β=(XTX+λI)−1XTy 可知 β \beta β是 λ \lambda λ的函数,当 λ ∈ [ 0 , ∞ ) \lambda \in [0,\infty) λ∈[0,∞)时,在平面直角坐标系中的 β − λ \beta-\lambda β−λ曲线称为岭迹曲线。当 β \beta β趋于稳定的点就是所要寻找的 λ \lambda λ值。
import pandas as pd
import numpy as np
from sklearn import model_selection
from sklearn.linear_model import Ridge
import matplotlib.pyplot as plt
data=pd.read_excel(r'C:\Users\Administrator\Desktop\diabetes.xlsx')
#拆分为训练集和测试集
predictors=data.columns[:-1]
x_train,x_test,y_train,y_test=model_selection.train_test_split(data[predictors],data.Y,
test_size=0.2,random_state=1234)
#构造不同的lambda值
Lambdas=np.logspace(-5,2,200)
#存放偏回归系数
ridge_cofficients=[]
for Lambda in Lambdas:
ridge=Ridge(alpha=Lambda,normalize=True)
ridge.fit(x_train,y_train)
ridge_cofficients.append(ridge.coef_)
#绘制岭迹曲线
plt.rcParams['font.sans-serif']=['Microsoft YaHei']
plt.rcParams['axes.unicode_minus']=False
plt.style.use('ggplot')
plt.plot(Lambdas,ridge_cofficients)
#x轴做对数处理
plt.xscale('log')
plt.xlabel('Log(Lambda)')
plt.ylabel('Cofficients')
plt.show()
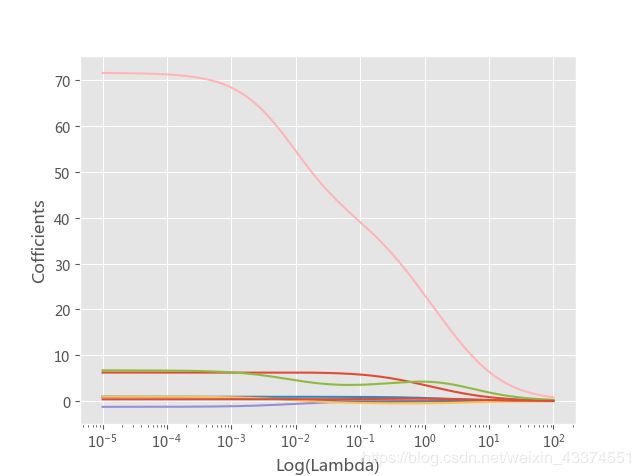
书上说在0.01附近大多数回归系数就趋于稳定,这哪看得出?所以定性的方法一般不太靠谱,还是用定量的方法吧!
(2)交叉验证法确定 λ \lambda λ值
交叉验证法的思想是,将数据集拆分为k个数据组(每组样本量大体相当),从k组中挑选k-1组用于模型的训练,剩下的1组用于模型的测试,则会有k-1个训练集和测试集配对,每一种训练集和测试集下都会有对应的一个模型及模型评分(如均方误差),进而可以得到一个平均评分。对于 λ \lambda λ值则选择平均评分最优的 λ \lambda λ值。
RidgeCV(alphas=(0.1, 1.0, 10.0), fit_intercept=True, normalize=False, scoring=None, cv=None, gcv_mode=None, store_cv_values=False)
• lambdas:用于指定多个 λ \lambda λ值的元组或数组对象,默认包含0.1,1,10三种值。
• fit_intercept:bool类型,是否需要拟合截距项,默认为True。
• normalize:bool类型,建模时是否对数据集做标准化处理,默认为False。
• scoring:指定用于模型评估的度量方法。
• cv:指定交叉验证的重数。
• gcv_mode:指定广义交叉验证的方法。
• store_cv_values:bool类型,是否保存每个 λ \lambda λ下交叉验证的评估信息,默认为False,只有cv为None时有效。
import pandas as pd
import numpy as np
from sklearn import model_selection
from sklearn.linear_model import RidgeCV
data=pd.read_excel(r'C:\Users\Administrator\Desktop\diabetes.xlsx')
#拆分为训练集和测试集
predictors=data.columns[:-1]
x_train,x_test,y_train,y_test=model_selection.train_test_split(data[predictors],data.Y,
test_size=0.2,random_state=1234)
#构造不同的lambda值
Lambdas=np.logspace(-5,2,200)
#设置交叉验证的参数,使用均方误差评估
ridge_cv=RidgeCV(alphas=Lambdas,normalize=True,scoring='neg_mean_squared_error',cv=10)
ridge_cv.fit(x_train,y_train)
print(ridge_cv.alpha_)
![]()
得到的结果是0.135
3.代码实现
Ridge(alpha=1.0, fit_intercept=True, normalize=False, copy_X=True, max_iter=None, tol=0.001, solver=‘auto’, random_state=None)
• alpha:用于指定 λ \lambda λ值参数,默认为1。
• fit_intercept:bool类型,是否需要拟合截距项,默认为True。
• normalize:bool类型,建模时是否对数据集做标准化处理,默认为False。
• copy_X:bool类型,是否复制自变量X的数值,默认为True。
• max_iter:指定模型的最大迭代次数。
• solver:指定模型求解最优化问题的算法,默认为’auto’。
• random_state:指定随机生成器的种子。
import pandas as pd
import numpy as np
from sklearn import model_selection
from sklearn.linear_model import Ridge,RidgeCV
from sklearn.metrics import mean_squared_error
data=pd.read_excel(r'C:\Users\Administrator\Desktop\diabetes.xlsx')
data=data.drop(['AGE','SEX'],axis=1)
#拆分为训练集和测试集
predictors=data.columns[:-1]
x_train,x_test,y_train,y_test=model_selection.train_test_split(data[predictors],data.Y,
test_size=0.2,random_state=1234)
#构造不同的lambda值
Lambdas=np.logspace(-5,2,200)
#设置交叉验证的参数,使用均方误差评估
ridge_cv=RidgeCV(alphas=Lambdas,normalize=True,scoring='neg_mean_squared_error',cv=10)
ridge_cv.fit(x_train,y_train)
#基于最佳lambda值建模
ridge=Ridge(alpha=ridge_cv.alpha_,normalize=True)
ridge.fit(x_train,y_train)
#打印回归系数
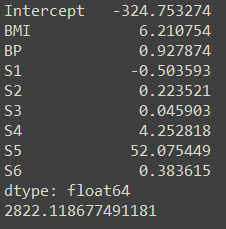
print(pd.Series(index=['Intercept']+x_train.columns.tolist(),
data=[ridge.intercept_]+ridge.coef_.tolist()))
#模型评估
ridge_pred=ridge.predict(x_test)
#均方误差
MSE=mean_squared_error(y_test,ridge_pred)
print(MSE)
二、LASSO回归
1.参数推导
岭回归无法剔除变量,而LASSO回归模型,将惩罚项由L2范数变为L1范数,可以将一些不重要的回归系数缩减为0,达到剔除变量的目的。
J ( β ) = ∑ ( y − X β ) 2 + λ ∣ ∣ β ∣ ∣ 1 = ∑ ( y − X β ) 2 + ∑ λ ∣ β ∣ = E S S ( β ) + λ l 1 ( β ) J(\beta)=\sum(y-X\beta)^2+\lambda||\beta||_1\\\text {\qquad\;\;\;\,}=\sum(y-X\beta)^2+\sum\lambda|\beta|\\=ESS(\beta)+\lambda l_1(\beta) J(β)=∑(y−Xβ)2+λ∣∣β∣∣1=∑(y−Xβ)2+∑λ∣β∣=ESS(β)+λl1(β)其中 E S S ( β ) = ESS(\beta)= ESS(β)=表示误差平方和, λ l 1 ( β ) \lambda l_1(\beta) λl1(β)表示惩罚项。由于惩罚项变成了绝对值,则在零点处就不可导,故采用坐标下降法(对于p维参数的可微凸函数 J ( β ) J(\beta) J(β),如果存在 β ^ \hat\beta β^使得 J ( β ) J(\beta) J(β)在每个坐标轴上均达到最小值,则 J ( β ) ^ \hat{J(\beta)} J(β)^就是点 β ^ \hat\beta β^上的全局最小值),控制其他p-1个参数不变,对目标函数中的某一个 β j \beta_j βj求偏导,以此类推对剩下的p-1个参数求偏导,最终令每个分量下的导函数为0,得到使目标函数达到全局最小的 β ^ \hat\beta β^。
E S S ( β ) = ∑ i = 1 n ( y i − ∑ j = 1 p β x i j ) 2 = ∑ i = 1 n ( y i 2 + ( ∑ j = 1 p β j x i j ) 2 − 2 y i ( ∑ j = 1 p β j x i j ) ) ESS(\beta)=\sum_{i=1}^{n}{\left(y_i-\sum_{j=1}^{p}{\beta x_{ij}}\right)^2 }\\=\sum_{i=1}^{n}{\left(y_i^2+\left(\sum_{j=1}^{p}{\beta_j x_{ij}}\right)^2-2y_i\left(\sum_{j=1}^{p}{\beta_j x_{ij}}\right)\right)} ESS(β)=i=1∑n(yi−j=1∑pβxij)2=i=1∑n⎝⎛yi2+(j=1∑pβjxij)2−2yi(j=1∑pβjxij)⎠⎞
⇒ ∂ E S S ( β ) ∂ β j = − 2 ∑ i − 1 n x i j ( y i − ∑ j = 1 p β j x i j ) = − 2 ∑ i − 1 n x i j ( y i − ∑ k ≠ j β k x i k − β j x i j ) = − 2 ∑ i − 1 n x i j ( y i − ∑ k ≠ j β k x i k ) + 2 β j ∑ i = 1 n x i j 2 = − 2 m j + 2 β j n j \Rightarrow\frac{\partial ESS(\beta)}{\partial\beta_j}=-2\sum_{i-1}^{n}{x_{ij}\left(y_i-\sum_{j=1}^{p}{\beta_jx_{ij}}\right)}\\\text{\qquad\qquad\qquad\qquad\quad\;\;}=-2\sum_{i-1}^{n}{x_{ij}\left(y_i-\sum_{k\neq j}^{}{\beta_kx_{ik}-\beta_jx_{ij}}\right)}\\\text{\qquad\qquad\qquad\qquad\qquad\;\,}=-2\sum_{i-1}^{n}{x_{ij}\left(y_i-\sum_{k\neq j}^{}{\beta_kx_{ik}}\right)}+2\beta_j\sum_{i=1}^{n}{x_{ij}^2}\\\text{\,}=-2m_j+2\beta_jn_j ⇒∂βj∂ESS(β)=−2i−1∑nxij(yi−j=1∑pβjxij)=−2i−1∑nxij⎝⎛yi−k̸=j∑βkxik−βjxij⎠⎞=−2i−1∑nxij⎝⎛yi−k̸=j∑βkxik⎠⎞+2βji=1∑nxij2=−2mj+2βjnj其中 m j = ∑ i − 1 n x i j ( y i − ∑ k ≠ j β k x i k ) , n j = ∑ i = 1 n x i j 2 m_j=\sum_{i-1}^{n}{x_{ij}\left(y_i-\sum_{k\neq j}^{}{\beta_kx_{ik}}\right)},n_j=\sum_{i=1}^{n}{x_{ij}^2} mj=∑i−1nxij(yi−∑k̸=jβkxik),nj=∑i=1nxij2
惩罚项不可导,则使用次导数:
∂ λ l 1 ( β ) ∂ β j = { λ , 当 β j > 0 [ − λ , λ ] , 当 β j = 0 − λ , 当 β j < 0 \frac{\partial\lambda l_1(\beta)}{\partial\beta_j}= \begin{cases} \lambda,\text{\qquad\;}当\beta_j>0\\ [-\lambda,\lambda],当\beta_j=0\\ -\lambda,\text{\quad\;\;}当\beta_j<0 \end{cases} ∂βj∂λl1(β)=⎩⎪⎨⎪⎧λ,当βj>0[−λ,λ],当βj=0−λ,当βj<0于是令两个偏导数相加等于0
∂ E S S ( β ) ∂ β j + ∂ λ l 1 ( β ) ∂ β j = { − 2 m j + 2 β j n j + λ = 0 [ − 2 m j − λ , − 2 m j + λ ] = 0 − 2 m j + 2 β j n j − λ = 0 \frac{\partial ESS(\beta)}{\partial\beta_j}+\frac{\partial \lambda l_1(\beta)}{\partial\beta_j}= \begin{cases} -2m_j+2\beta_jn_j+\lambda=0\\ [-2m_j-\lambda,-2m_j+\lambda]=0\\ -2m_j+2\beta_jn_j-\lambda=0 \end{cases} ∂βj∂ESS(β)+∂βj∂λl1(β)=⎩⎪⎨⎪⎧−2mj+2βjnj+λ=0[−2mj−λ,−2mj+λ]=0−2mj+2βjnj−λ=0 ⇒ β j = { ( m j − λ 2 ) / n j , 当 m j > λ 2 0 , 当 m j ∈ [ − λ 2 , λ 2 ] ( m j + λ 2 ) / n j , 当 m j < λ 2 \Rightarrow\beta_j= \begin{cases} (m_j-\dfrac{\lambda}{2})/n_j,当m_j>\dfrac{\lambda}{2}\\[2ex] 0,\text{\qquad\qquad\quad\;}当m_j\in[-\dfrac{\lambda}{2},\dfrac{\lambda}{2}]\\[2ex] (m_j+\dfrac{\lambda}{2})/n_j,当m_j<\dfrac{\lambda}{2} \end{cases} ⇒βj=⎩⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎧(mj−2λ)/nj,当mj>2λ0,当mj∈[−2λ,2λ](mj+2λ)/nj,当mj<2λ
2. λ \lambda λ的选择
直接使用交叉验证法
LassoCV(eps=0.001, n_alphas=100, alphas=None, fit_intercept=True, normalize=False, precompute=‘auto’, max_iter=1000, tol=0.0001, copy_X=True, cv=None, verbose=False, n_jobs=1, positive=False, random_state=None, selection=‘cyclic’)
• eps:指代 λ \lambda λ最小值与最大值的商,默认为0.001。
• n_alphas:指定 λ \lambda λ的个数,默认为100个。
• alphas:指定具体的 λ \lambda λ列表用于模型的运算。
• fit_intercept:bool类型,是否需要拟合截距项,默认为True。
• normalize:bool类型,建模时是否对数据集做标准化处理,默认为False。
• precompute:bool类型,是否在建模前计算Gram矩阵提升运算速度,默认为False。
• max_iter:指定模型的最大迭代次数。
• tol:指定模型收敛的阈值,默认为0.0001。
• copy_X:bool类型,是否复制自变量X的数值,默认为True。
• cv:指定交叉验证的重数。
• verbose:bool类型,是否返回模型运行的详细信息,默认为False。
• n_jobs:指定使用的CPU数量,默认为1,如果为-1表示所有CPU用于交叉验证的运算。
• positive:bool类型,是否将回归系数强制为正数,默认为False。
• random_state:指定随机生成器的种子。
• selection:指定每次迭代选择的回归系数,如果为’random’,表示每次迭代中将随机更新回归系数;如果为’cyclic’,则每次迭代时回归系数的更新都基于上一次运算。
import pandas as pd
import numpy as np
from sklearn import model_selection
from sklearn.linear_model import LassoCV
data=pd.read_excel(r'C:\Users\Administrator\Desktop\diabetes.xlsx')
#拆分为训练集和测试集
predictors=data.columns[:-1]
x_train,x_test,y_train,y_test=model_selection.train_test_split(data[predictors],data.Y,
test_size=0.2,random_state=1234)
#构造不同的lambda值
Lambdas=np.logspace(-5,2,200)
#设置交叉验证的参数,使用均方误差评估
lasso_cv=LassoCV(alphas=Lambdas,normalize=True,cv=10,max_iter=10000)
lasso_cv.fit(x_train,y_train)
print(lasso_cv.alpha_)
![]()
3.代码实现
Lasso(alpha=1.0, fit_intercept=True, normalize=False, precompute=False, copy_X=True, max_iter=1000, tol=0.0001, warm_start=False, positive=False, random_state=None, selection=‘cyclic’)
• alphas:指定 λ \lambda λ值,默认为1。
• fit_intercept:bool类型,是否需要拟合截距项,默认为True。
• normalize:bool类型,建模时是否对数据集做标准化处理,默认为False。
• precompute:bool类型,是否在建模前计算Gram矩阵提升运算速度,默认为False。
• copy_X:bool类型,是否复制自变量X的数值,默认为True。
• max_iter:指定模型的最大迭代次数。
• tol:指定模型收敛的阈值,默认为0.0001。
• warm_start:bool类型,是否将前一次训练结果用作后一次的训练,默认为False。
• positive:bool类型,是否将回归系数强制为正数,默认为False。
• random_state:指定随机生成器的种子。
• selection:指定每次迭代选择的回归系数,如果为’random’,表示每次迭代中将随机更新回归系数;如果为’cyclic’,则每次迭代时回归系数的更新都基于上一次运算。
import pandas as pd
import numpy as np
from sklearn import model_selection
from sklearn.linear_model import Lasso,LassoCV
from sklearn.metrics import mean_squared_error
data=pd.read_excel(r'C:\Users\Administrator\Desktop\diabetes.xlsx')
data=data.drop(['AGE','SEX'],axis=1)
#拆分为训练集和测试集
predictors=data.columns[:-1]
x_train,x_test,y_train,y_test=model_selection.train_test_split(data[predictors],data.Y,
test_size=0.2,random_state=1234)
#构造不同的lambda值
Lambdas=np.logspace(-5,2,200)
#设置交叉验证的参数,使用均方误差评估
lasso_cv=LassoCV(alphas=Lambdas,normalize=True,cv=10,max_iter=10000)
lasso_cv.fit(x_train,y_train)
#基于最佳lambda值建模
lasso=Lasso(alpha=lasso_cv.alpha_,normalize=True,max_iter=10000)
lasso.fit(x_train,y_train)
#打印回归系数
print(pd.Series(index=['Intercept']+x_train.columns.tolist(),
data=[lasso.intercept_]+lasso.coef_.tolist()))
#模型评估
lasso_pred=lasso.predict(x_test)
#均方误差
MSE=mean_squared_error(y_test,lasso_pred)
print(MSE)

相对于岭回归而言,可以看到LASSO回归剔除了两个变量,降低了模型的复杂度,同时减少了均方误差,提高了模型的拟合效果。
参考文献:
[1]Peter Harrington.《机器学习实战》.人民邮电出版社,2013-6
[2]刘顺祥.《从零开始学Python数据分析与挖掘》.清华大学出版社,2018