数据结构|二叉树的顺序存储和堆排序

目录

 

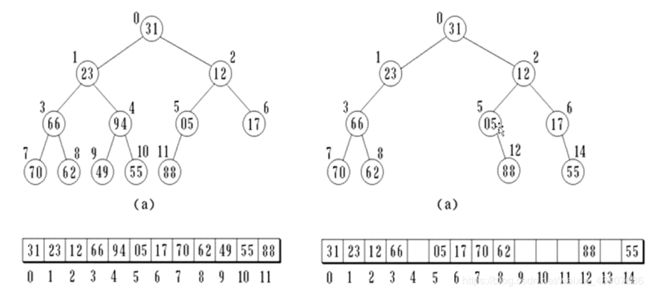
一.二叉树的顺序存储

1.规则

2.二叉树的遍历

2.1中序遍历

2.由顺序结构构建链式二叉树

3.由链式创建顺序二叉树。

4.由链式二叉树构建中序双链表

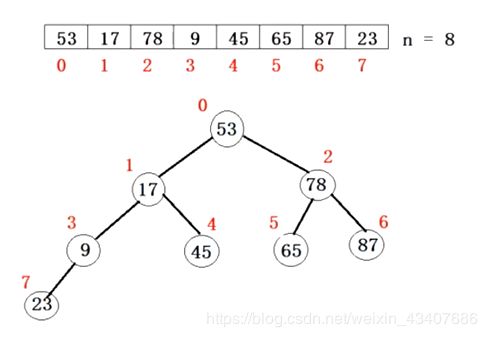
二.堆排序与优先级队列

1.最小堆的调整过程

2.优先级队列（堆排序实现）

---

一.二叉树的顺序存储

1.规则

2.二叉树的遍历

2.1中序遍历

思想：跟链式存储的遍历方式一样，左右跟

void InOrder(ElemType*ar,int i,int n)
{
	if(i

非递归的方式：跟链式的方法类似，借用一个栈 ，二叉树的根节点入栈，左子树依次入栈，如果左子树为空，出栈顶元素，打印栈顶元素，一个右子树入栈，循环上述过程。终止条件，栈为空或者i >= n（下标超过结点个数，越界）。

void NiceOrder(ElemType *ar,int n)//n为结点个数
{
	if(NULL == ar || n < 1) return;
	stack st;
	int i = 0;
	while(!st.empty() || i < n)
	{
		while(i < n && ar[i]!=END)//i

2.由顺序结构构建链式二叉树

思想：利用中序遍历的方式将顺序结构中的结点赋值给链式二叉树

struct BtNode *Create(ElemType *br,int i,int n)
{
	struct BtNode *s = NULL;
	if(br[i]!=END && i < n)
	{
		s = Buynode();
		s->data = br[i];
		s->leftchild = Create(br,2*i+1,n);
		s->rightchild = Create(br,2*i+2,n);
	}
	return s;
}
struct BtNode *CreateAr(ElemType *br,int n)
{
	struct BtNode *s = NULL;
	if(br != NULL && n>0)
	{
		s = Create(br,0,n);
	}
	return s;
}

3.由链式创建顺序二叉树。

void LinkArray(struct BtNode* ptr,ElemType *br,int i) //将ptr对应的数值放到数组中
{
	if(ptr!=NULL)
	{
		br[i] = ptr->data;
		LinkArray(ptr->leftchild,br,i*2+1);
		LinkArray(ptr->rightchild,br,i*2+2);
		
	}
}
int main()
{
	int ar[] = {31,23,12,66,-1,5,17,70,62,-1,-1,-1,88,-1,55};
	int br[] = {-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1,-1};
	int n = sizeof(ar)/sizeof(ar[0]);
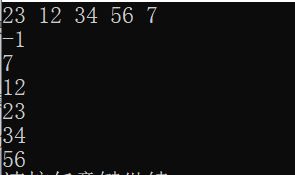
	InOrder_Ar(ar,n);//中序遍历
	cout<

4.由链式二叉树构建中序双链表

二.堆排序与优先级队列

最小堆的特点，每个根结点都小于它的左孩子和右孩子。

最大堆特点：每个根节点都大于它的左孩子和右孩子。

1.最小堆的调整过程

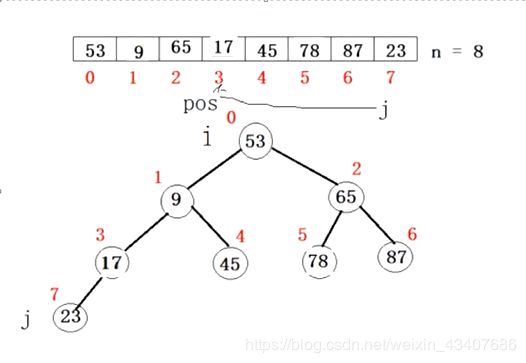
步骤（1)最后一个结点的下标j为7，它的根节点i下标为（j-1）/2 = 3,将i结点的值取出来，j没有右孩子，i < j  将i放到原位置。

i - 1等于2，将i结点的值取出来给tmp，j = 5，j比右孩子小，再将tmp的值与 j结点的值比较，j结点的值更小，将j 结点的值给i结点。i = j = 5，j = 11，超出数组的最大下标，退出，i结点的值 = tmp。

i - 1 = 1,j = 2* i + 1 = 3,tmp = i结点的值为17,j结点的值比它的右孩子结点的值小，j结点的值与tmp 比较，j更小，j结点的值给i结点，i = j = 3, j = 7, j结点的值大于tmp退出，i结点的值 = tmp。

得到下图所示的结果：

i - 1 = 0,现在开始从0结点开始调整。

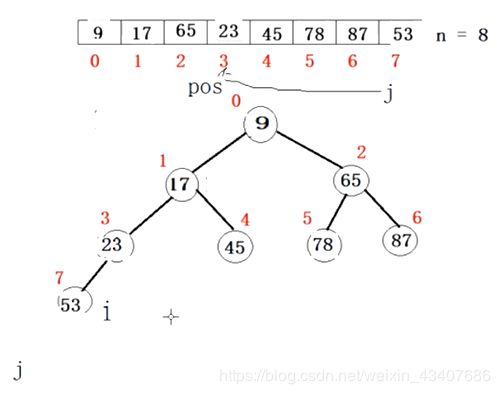
步骤（2)从0开始调整

i = 0，tmp = 0结点的值=53， j = i*2+1 = 1，j->data < tmp ,i->data = j->data。

i = j = 1, j = 3,j->data = 17,17

i = j = 3,j = 7,j->data = 23,23

i = j = 7,j = 15,越界，退出

i结点的值为tmp(53)

最终结果如下图所示：

void FilterDown(int *ar,int begin,int end)//从上向下调整
{
	int i = begin,j = 2*i+1;//leftchild
	int tmp = ar[i];
	while(j <= end)//
	{
		if(j < end && ar[j] > ar[j+1])//ar[j+1]为右子树,j < end,j+1才不会超出范围
		++j;
		if(ar[j] < tmp)
		{
			ar[i] = ar[j];
		}
		else
		{
			break;
		}
		i = j;
		j = i * 2 + 1;
	}
	ar[i] = tmp;
}

void HeapSort(int *ar,int n)
{
	if(NULL == ar || n < 2)  return;
	int end = n-1;//最后一个元素的下标
	int pos = (end - 1)/2;//第一个分支的根节点
	while(pos >= 0)//建堆
	{
		FilterDown(ar,pos,end);
		--pos;
	}
	
	while(end > 0)//将数组ar从大到小排序,将ar[0]与ar[end]交换，然后在将ar[0]-ar[end-1]按照最小堆排序
	{
		swap(ar[0],ar[end]);
		end = end - 1;
		FilterDown(ar,0,end);
	}
}
int  main()
{
	int ar[] = {53,17,78,9,45,65,87,23};
	int n = sizeof(ar)/sizeof(ar[0]);
	HeapSort(ar,n);
	return 0;
}

将ar数组排序后如下图所示：

 

2.优先级队列（堆排序实现）

1.在堆中插入元素的过程：

插入的元素在数组的最后一个位置，然后进行调整。下面用具体的例子来说明。

如在上面的图中插入5.

5的下标为8  ， j = 8,  i = (8-1)/2 = 3, tmp = ar[8],  ar[3] > tmp,所以ar[8] = ar[3] = 9.

j = i = 3, i = (j-1)/2 = 1,  17 > 5,所以将17放到ar[j]的位置

依次类推，直到 j = 0,tmp的值给ar[0]结束。

2.删除堆顶的元素

将最后一个元素赋给堆顶，然后用从上向下调整堆的函数

3.优先级队列代码实现

const int MAXSIZE = 100;
const int INCSIZE = 2;//增量为2
template
class PriQueue
{
	Type *data;//连续空间
	int maxsize;//元素的最大个数
	int cursize;//元素的当前个数
	void FilterDown(int begin,int end)//堆的从上向下调整
	{
		int i = begin;
		int j = i*2+1;
		Type tmp = data[i];
		while(j <= end)
		{
			if(j < end && data[j] > data[j+1])
				++j;
			if(tmp <= data[j])
				break;
			else
			{
				data[i] = data[j];
				i = j;
				j = i*2+1;
			}
		}
		data[i] = tmp;
	}
	void FilerUp(int end)//堆的从下向上调整,begin是插入的数字的下标位置
	{
		int j = end;
		int i = (j-1)/2;
		int tmp = data[j];
		while(j > 0)
		{
			if(tmp >= data[i])
				break;
			data[j] = data[i];
			j = i;
			i = (j-1)/2;
		}
		data[j] = tmp;
	}
	void Make_Heap()//建堆
	{
		int end = cursize - 1;
		int pos = (end - 1)/2;
		while(pos >= 0)
		{
			FilterDown(pos,end);
			--pos;
		}
	}
public:
	PriQueue():maxsize(MAXSIZE),cursize(0)//构造函数
	{
		data = new Type[maxsize];
	}
	PriQueue(Type *ar,int n)//带参构造函数
	{
		maxsize = n > MAXSIZE ? n : MAXSIZE;
		cursize = n;
		data = new Type[maxsize];
		for(int i = 0;i < n;++i)
		{
			data[i] = ar[i];//把数据放入到数组
		}
		Make_heap();//建堆
		//另外一种建堆方式
		/*for(int i = 0;i < n;++i)
		{
			push(data[i]);
		}*/
	}
	~PriQueue()
	{
		delete []data;
		data = NULL;
		maxsize = 0;
		cursize = 0;
	}

	int GetSize() const//结点个数
	{
		return cursize;
	}
	bool IsEmpty() const
	{
		return GetSize() == 0;
	}
	Type & GetFront() const//取堆顶元素
	{
		return data[0];
	}
	/*const Type & GetFront() const//取队头元素
		{
		   return data[0];
	    }*/
	void Pop()//删除堆顶元素
	{
		data[0] = data[cursize-1];
		--cursize;
		FilterDown(0,cursize-1);

	}
	void Push(const Type &x)//入队列
	{
		if(cursize >= maxsize) return;
		data[cursize] = x;
		FilerUp(cursize);
		++cursize;
	}
};
int main()
{
	PriQueue qu;
	int x;
	while(cin>>x,x!=-1)
	{
		qu.Push(x);
	}
	while(!qu.IsEmpty())
	{
		int x = qu.GetFront();
		qu.Pop();
		cout<

每次取堆顶（最小数）代码截图：