leetcode-搜索专题

1. 关于搜索

在leetcode上，搜索一般只会涉及BFS和DFS，所以本文仅仅关注这俩个。并给出一些我对搜索的理解，代码都是类似c++的伪代码。

1.1 BFS和DFS小谈

这里给出俩中搜索的模板，如果是第一次接触的话，这里仅仅对俩个模板有印象就可以了。后面会遇到具体的题，再回来看这里的模板。就非常有意思了。

1.1.1 BFS模板

void bfs()
	queue.push(start)
	while(queue.size())
		step++
		for i : queue.size()
			curr = queue.pop()
			for eachChild : findChilds(curr)
				if !isVisited(eachChild)
					queue.push(eachChild)					

简单注释下：
bfs的要点就是记录每次横向的长度。将我们的遍历分为一层，一层。一般情况下，会用到step来记录每一层。

1.1.2 DFS模板

dfs比较灵活，但是最常用的还是如下参数
d: 表示迭代深度
maxDepth: 表示最大迭代深度
path: 表示当前迭代的路径
res: 一般为结果集

res
void dfs(currVal, d, maxDepth,  path)
	if(d == maxDepth)
		res.push_back(path)
		return
	for eachChild : findChilds(currVal)
		... // 可能有一些判断条件
		path.push_back(eachChild)
		dfs(eachChild, d+1, maxDepth, path)
		path.pop_back();

2. 题目一览

这里盗用一个B站up主的图，花花酱leetcode，我的很多思路都是和他学的。

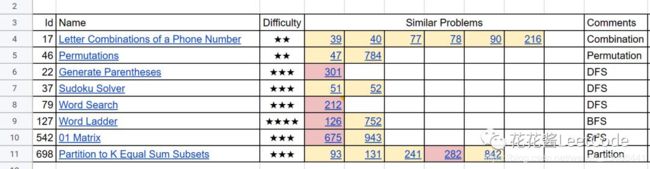
2.1 排列和组合问题

2.1.1 排列问题

1. 综述

排列问题这里我简单描述小，就是n个元素换位置的问题。明白排列问题是什么比较简单，但难的是如何看出哪些是排列问题。

2. 送上来的排列问题

leetcode-47-全排列
你会发现，大部分的排列问题都会在此基础上变化。

class Solution {
public:
    vector<vector<int>> permute(vector<int>& nums) {
        vector<vector<int>> res;
        vector<bool> isVisited(nums.size(), false);
        vector<int> path;
        dfs(nums, isVisited, 0, path, res);
        return res;
    }
    void dfs(const vector<int>&nums, vector<bool>&isVisited, int d, vector<int>&path, vector<vector<int>>& res)
    {
        if(d == nums.size())
        {
            res.push_back(path);
            return;
        }
        for(int i = 0; i < isVisited.size(); i++)
        {
            if(isVisited[i])
                continue;
            path.push_back(nums[i]);
            isVisited[i] = true;
            dfs(nums, isVisited, d+1, path, res);
            isVisited[i] = false;
            path.pop_back();
        }
    }
};

1. 排列问题是因为要保留路径，所以dfs是非常好的选择。
2. dfs的本质我认为是选择问题，或者说建树或者图的问题。给定一个节点。做出选择的本质实际上就是在找它的子节点。

比如说，给定[1 2 3 4]的排列。我第一次的选择是(1 2 3 4)，当我选择1之后，只有(2 3 4)供我选择。如很多地方见到的图片——下图。

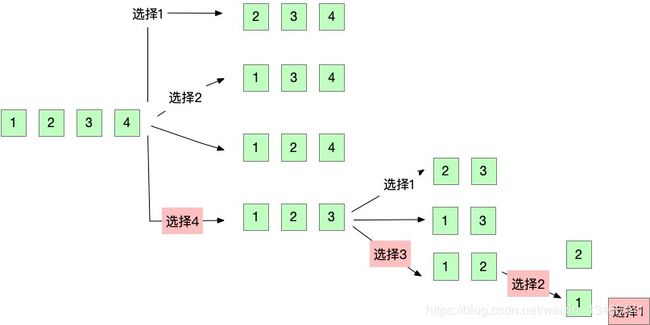
以上得到1个 [4 3 2 1]的一种排列。
3. 排列问题在于，选择池大小是变化的。当拿走一种选择后，剩下的选择池会变小。所以我们利用isVisited记录自己已经选择过哪些。
4. 回溯，这个点一旦理解了就非常简单，我觉得在这里想象一下非常好。这些一切的变量都是一种状态。表明你已经选择了[4 3 2 1]，那么如何做下一个选择呢。就是回溯一下状态。[4 3] 此时你可以选择1而不是2，即[4 3 1 2]。而这个恰恰和递归是完美结合的。建议，利用gdb或者lldb一步一步推下程序，画出状态图，就很容易理解。

2.1.2 组合问题

1. 综述

组合问题一般都是子集问题。其有俩种思路理解。具体到题吧。

2. 问题

组合的问题一般可以这样出。

1. 给出所以不重复子集
   leetcode-78-子集
2. 给出给定长度为K的所有不重复子集
   leetcode-77-组合

2.1 子集问题

思路1:
依然看做是选择问题，针对[1 2 3 4]，对于排列来说，每次必须要选择一个数字。但对于组合来说，每次只有俩个选择，这个数选还是不选。这个思路一般比较容易想出，而且很容易理解。

class Solution {
public:
    vector<vector<int>> subsets(vector<int>& nums) {
        vector<vector<int>> vec_res;
        backtrack(nums, 0, vector<int>{}, vec_res);
        return vec_res;
    }
    
    void backtrack(vector<int> &nums, int k, vector<int> a_sol, vector<vector<int>> &res)
    {
        if(k >= nums.size())
        {
            res.push_back(a_sol);
        }
        else{
            for(int i = 0; i < 2; ++i)
            {
                if(i)
                    a_sol.push_back(nums[k]);
                backtrack(nums, k+1, a_sol, res);
                if(i)
                    a_sol.pop_back();
            }
        }
    }
};

思路2：
状态问题，得到所有组合的本质实际上就是得到所有状态的问题。所以利用BFS或者DFS记录每一个状态即可。或者也可以这样理解，针对每一层，比如是[1 2 3 4]，对于第一层来说，有如下选项，不选或者[1 2 3 4]任选其1。

class Solution {
public:
    vector<vector<int>> subsets(vector<int>& nums) {
        vector<vector<int>> res;
        dfs(nums, 0, vector<int>{}, res);        
        return res;
    }
    
    void dfs(const vector<int>&nums, int start, vector<int> ans, vector<vector<int>> &res){
        res.push_back(ans);
        for(int i = start; i < nums.size(); i++){
            ans.push_back(nums[i]);
            dfs(nums, i + 1, ans, res);
            ans.pop_back();
        }
    }
};

2.2. 终极思考

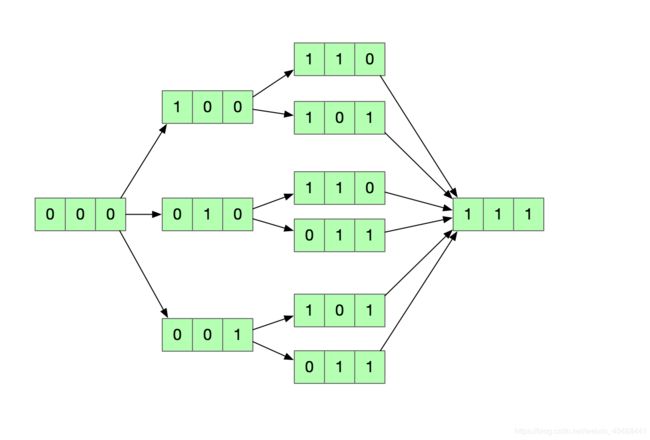
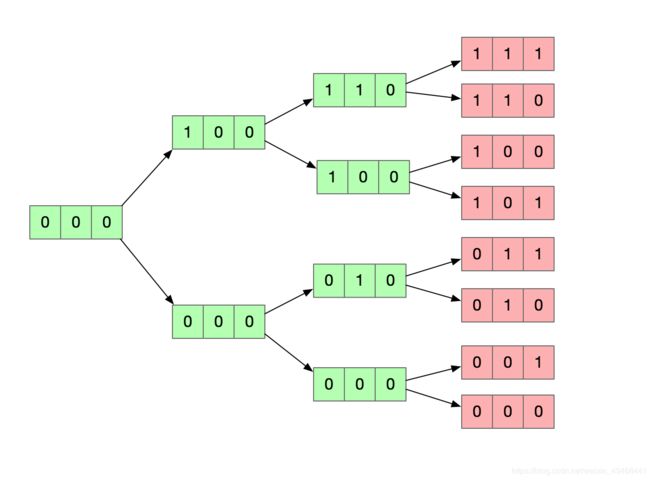
假设我们用0来表示没有选择一个数，用1来表示选择了一个数。那么这个问题可以变化为这样。比如是[1 2 3]

1. 子集问题就会变成由000 -> 111的所有状态。

利用遍历状态得到所有子集

利用选择得到所有子集

我们发现一个相同点，就是结果集和对应的10进制数恰好是0-7。所以我们可以直接构造结果集所有状态，然后利用映射来得到所有结果集。

class Solution {
public:
    vector<vector<int>> subsets(vector<int>& nums) {
        int n = nums.size();
        int size = ((1 << n) - 1);
        vector<vector<int>> res;
        res.push_back({});
        for(int status = 0; status <= size; status++) // 遍历所有状态
        {
            vector<int> tmp;
            for(int i = 0; i < nums.size(); i++) // 根据状态映射结果集
            {
                if((1 << i) & status)
                {
                    tmp.push_back(nums[i]);
                }
            }
            if(tmp.size())
            res.push_back(tmp);
        }
        return res;
    }
};

2.2 固定长度子集问题

这个问题算是简化版本的子集问题。实际上就是由原来的n个选择，变为了k个，但是递归深度不变。当选择了k个后，剩下的就是默认为不选择。

2.3 回溯问题

回溯问题，没什么可谈的，就是在dfs的基础上扩展。
这里练习的主要就是剪枝问题。如何剪枝这个只能看个人思考。

2.4 BFS问题

bfs也没什么可谈的，使用模板都可以解决，一般都是用来寻找最短路径的。值得注意的就是双向BFS来寻找最短路径。

2.5 Partition问题

分治的本质就像小时候数学里的插点一样。给定一行元素。插点，将左边分为新的问题，将右边分为新问题，可能这就是划分的理解么。这里的重点是准确寻找递归基，即递归返回的条件。
分治

利用map加快字符串转化

遇到很多字符串转整数的问题，可以字符串判断是否是回文的，这里因为涉及到重复，都可以用map来加快速度。

leetcode‍♂️

最近时间比较忙，接下来就是准备Redis的学习了，leetcode可能会减少到一周2题吧。也就不发了。