GCN推导

GCN涉及到的理论比较多，包括信号分析中的傅里叶变换、图谱等理论，这里只做一个简单的推导，旨在让读者了解GCN推导的大致思路以及其中用到的定理，错误之处还请指出。大致了解GCN的思路后可移步学习其中涉及到的理论知识：

• 如何理解图卷积
• 图卷积网络 GCN Graph Convolutional Network

由于图是不规则化的非欧式结构数据，而CNN是在欧式数据（如图片、语音等）上进行卷积，如何在不规则的图上定义卷积？我们从卷积定理入手。

卷积定理

卷积定理：函数卷积的傅里叶变换是函数傅立叶变换的乘积

这个定理十分关键，假设有两个函数$f$和$g$，$F$代表傅里叶变换，$F^{(-1)}$为傅里叶逆变换，$f\ast g$为函数$f$与$g$的卷积，则根据卷积定理
$$F(f\ast g)=F(f)\cdot F(g)\Rightarrow f\ast g=F^{(-1)}\{F(f)\cdot F(g)\}$$
这表明卷积运算可以拆分为：傅里叶变换、傅里叶逆变换、乘积，乘积运算很简单，所以在图上定义卷积的关键是 如何定义图的傅里叶变换和傅里叶逆变换。

图的傅里叶变换

参考自傅里叶分析（强烈推荐）
傅里叶变换的简单理解（有点上升到哲学）

• 时域：我们所处的真实世界，以时间作为参照来观察动态的世界。
• 频域：“世界是永恒不变的”，世界是静止的。

傅里叶变换就是将函数从时域变换到频域中。很多在时域看似不可能做到的数学操作在频域反而很容易，例如卷积定理，在时域中卷积比较困难，但是通过傅里叶变换到频域中就只需要做一个简单的乘积操作，再将结果傅里叶逆变换回来就可以得到时域中的卷积。
传统的傅里叶变换定义为：
$$F(w)=F[f(x)]=\int f(x)e^{(-iwx)}dx$$

其中$w$是频率，而傅里叶的逆变换为：
$$f(x)=\int F(w)e^{iwx}dw$$
可以看到对函数（在信号分析中又称为信号）$f(x)$的傅里叶变换本质上就是将$f(x)$映射到以$e^{(-iwx)}$为基向量的空间中。所以在图上定义傅里叶变换的关键是找到一组傅里叶变换的基，研究GSP(graph signal processing)的学者首先定义了图上的傅里叶变换，他们将传统傅里叶变换的基$e^{(-iwx)}$变为图的拉普拉斯矩阵L的特征向量。

为什么会找拉普拉斯矩阵？因为$e^{(-iwx)}$实际上是拉普拉斯算子$\Delta$的特征函数，对$x$求二阶导有
$$\Delta e^{(-iwx)}=\frac{{\partial }^2}{\partial x^2}{e}^{(-iwx)}=-w^2{e}^{(-iwx)}$$

可见$e^{(-iwx)}$是拉普拉斯算子$\Delta$的特征函数，$w$与特征值密切相关。所以学者便将$e^{(-iwx)}$与图的拉普拉斯矩阵联系在一起（图拉普拉斯矩阵实际上是离散的拉普拉斯算子），并将拉普拉斯矩阵的特征向量作为图傅里叶变换的基，特征值对应频率w。假设拉普拉斯矩阵为$L$（定义下一小节介绍），其特征分解为$L=U\Lambda U^{-1}=U\Lambda U^T$（这里$U$是正交矩阵，所以后面的等号成立），$U=(u_1,u_2,\dots ,u_n)$，$u_l$是$L$的第 $l$个特征向量，$\Lambda =diag({\lambda }_1,...,{\lambda }_N)$是特征值组成的对角矩阵。仿照传统傅里叶变换，图上的傅里叶变换定义为：
$$F({\lambda }_l)=\sum _{i=1}^{N}f(i)u_l(i)$$
$u_l(i)$代表$L$第$l$个特征向量的第$i$个分量，进一步将其写为矩阵的形式：

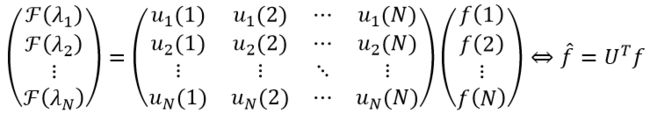
图的傅里叶逆变换为：
$$f=U\hat{f}$$

图拉普拉斯矩阵

图的拉普拉斯矩阵$L=D-A$，拉普拉斯矩阵的定义有几种，这是其中一种比较普遍的定义，$D$是顶点的度对角矩阵，$A$是图的邻接矩阵，拉普拉斯矩阵的定义只针对无向图，因此$L$是一个实对称矩阵，对其进行特征分解得到的矩阵$U$是正交的，所以它具备一组线性无关的正交基，因此可以作为傅里叶变换的基，还有很多其它性质，这里不详细介绍。

图卷积

以上分析得到两个重要结论：

• 卷积定理表明卷积运算可以拆分为傅里叶变换、傅里叶逆变换、乘积三个操作：$f\ast g=F^{-1}\{F(f)\cdot F(g)\}$
• 傅里叶变换分析得出图上的傅里叶变换定义为$\hat{f}=U^{T}f$，傅里叶逆变换为$f=U\hat{f}$。

综上可得图卷积的定义为：
$$(f\ast g{)}_G=U((U^{T}g)\cdot (U^{T}f))$$

其中$f$是节点输入特征，$g$是卷积核。因为$U^{T}g$和$U^{T}f$都是一个向量，因此也可以将其写为

$\hat{g}({\lambda }_i)$是$U^{T}g$中的第$i$个分量，两种写法是等价的。

深度学习中图卷积的三个重要演变过程

深度学习中的卷积就是要设计可以训练的卷积核，下面介绍3篇引用量很高的论文对图卷积的改进。

(1) Spectral Networks and Locally Connected Networks on Graphs. ICLR 2014
这篇文章第一次提出谱卷积神经网络，它直接将$g_{\theta }$作为可训练的卷积核：

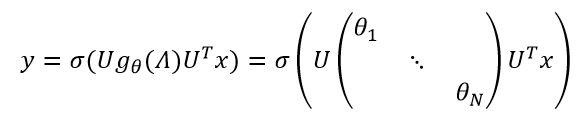
$\theta \in R^N$是可训练参数，$\sigma$是非线性激活函数，$x$是顶点的特征向量。

缺点：计算量很大，每一次传播都需要计算$U{g}_{\theta }(\Lambda )U^T$三个矩阵的乘积，对于大图而言不可行，且特征分解耗时；另外有$N$个参数，参数规模和图节点的规模一样多。

(2) Convolutional neural networks on graphs with fast localized spectral filtering. NIPS 2016

这篇文章(简称ChebNet)针对上述缺点巧妙设计了多项式卷积核：

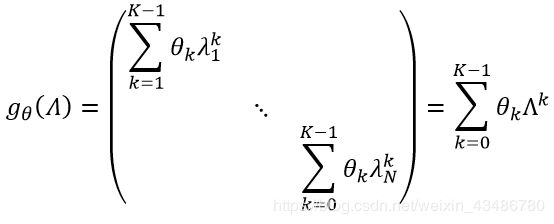
进而图卷积可写为：

可以发现现在参数只有K个，与节点个数N独立，参数的复杂度大大降低，且不需要对拉普拉斯矩阵进行特征分解。由于还要计算$L^k$，时间复杂度还是很高，因此作者用切比雪夫多项式（Chebyshev polynomial，这也是为什么称为ChebNet）对$L^k$进行$k$阶截断拟合，切比雪夫多项式的递归定义为：$$T_k(x)=2x{T}_{k-1}(x)-T_{k-2}(x),T_0=1,T_1=x$$且$x\in [-1,1]$。首先将L缩放到$[-1,1]$之间，得规范化拉普拉斯矩阵$L=\frac{2L}{{\lambda }_{max}}-I_n$，则：
$$x\ast g_{\theta }=\sum _{k=0}^{K-1}{\theta }_k{L}^{k}x\approx \sum _{k=0}^{K-1}{\theta }_k{T}_k(L)x$$
其中$T_0(L)=I_n，T_1(L)=L=\frac{2L}{{\lambda }_{max}}-I_{n}n$。

(3) GCN Semi-supervised classification with graph convolutional networks. ICLR 2017

这篇文章是引用量最高的一篇，它使用对称归一化的拉普拉斯矩阵$L=I_n-D^{-1/2}A{D}^{-1/2}$，并对ChebNet进行化简，令$K=2，{\lambda }_{max}=2$，则ChebNet变为：

为了防止过拟合，作者简化参数，令$\theta ={\theta }_0=-{\theta }_1$，得：
$$x\ast g_{\theta }=\theta (I_n+D^{-1/2}A{D}^{-1/2})x$$

另外由于$I_n+D^{-1/2}A{D}^{-1/2}$的特征值在$[0,2]$之间，重复叠加可能导致数值不稳定和梯度消失或爆炸，因此作者将其重整化为$I_n+D^{-1/2}A{D}^{-1/2}\to D^{-1/2}A{D}^{-1/2}$，其中$A=A+I_n，D_{ii}={\sum }_j{A}_{ij}$ 。最后就导出GCN的快速传播公式：
$$H^{(k)}=\sigma (\hat{A}{H}^{(k-1)}{W}^{(k)})$$
$H^{(k-1)}$是第k-1层的输出，$W^{(k)}$是第k层的卷积核，$\hat{A}=D^{-1/2}A{D}^{-1/2}$。