搜索算法——A*算法

简述

$A\ast$算法是优化过后的$bfs$算法，是一种启发式搜索，什么叫启发式搜索呢？它是利用问题拥有的启发信息来引导搜索，达到减少搜索范围、降低问题复杂度的目的（百度百科）
那是如何启发的呢？通过考虑两个因素，一个是已经行驶过的距离，一个是估计要行驶的距离。

首先来看一个最简单的$BFS$的算法的寻路过程，假设绿色的格子是起点，红色的格子是终点，我们来看一下$bfs$的扩展过程，熟悉bfs的都知道，首先将起点从队列中取出，每次将周围所有可到达的顶点加入队列中,不断重复这个过程，那么扩展出来的样子如下图

但是通过观察路径我们会发现，绿色格子的左边方向的格子是可完全不需要被扩展的，因为左边的部分肯定是无法到达终点的，可以直接剪去，该如何剪去呢？可以利用方格本身所带有的信息，
首先对于每一个走过的位置，可以记录两个取值，一个表示已经花费的实际代价$g(x)$，一个表示估计到达终点还需要花费的估计代价$h(x)$,那么对于起点格子周围的点，右边的点的$h(x)$肯定是小于左边的点的$h(x)$，因此扩展右边的点，那么对于每一个点，到达终点的最优的代价路径应该是$min(h(x)+g(x))$，这个就是$A\ast$当中的估价函数。
$$f(x)=h(x)+g(x)$$
很明显，对于每一次需要对当前结点进行扩展的时候，我们都应该选择估价函数的值最低的进行扩展（其中的$min(f(x))$的值是通过一个堆来实现的），其中$g(x)$表示已经走过的代价，是可以确定的，关键字在于如何计算$h(x)$的值，简单介绍两种计算$h(x)$的方法

• 欧几里得距离（欧氏距离）
  $d=\sqrt{(x_1-x_2{)}^2+(y_1-y_2{)}^2}$
• 曼哈顿距离（出租车距离）
  $d=|x_1-x_2|+|y_1-y_2|$

只有当$h(x)\le h$,(这里的$h$是实际距离)的时候，这样的估价函数才能够找到最短路径
经过优化之后的路径变成了这样（减去了上左下几个方向的扩展树）:

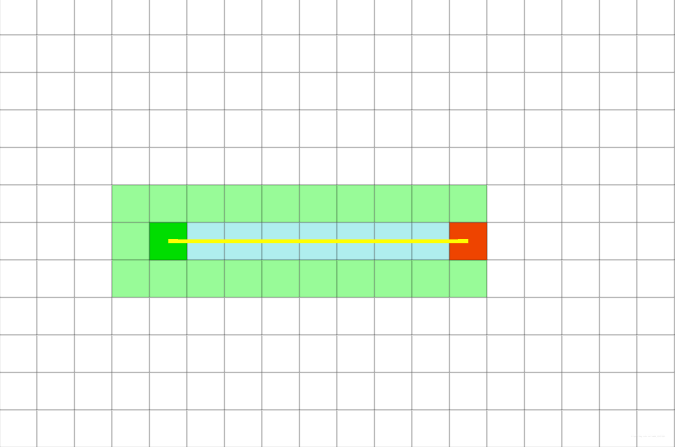
通过这样一个简单的例子，我们可以发现$bfs$算法，就是最糟糕情况下的$A\ast$，当$h(x)=0$的时候，$A\ast$就退化成了广度优先搜索,不具备任何启发信息，暴力扩展周围所有能够扩展的点。

贴一个超级简单的题，简单帮助理解$A\ast$

根据自己的理解找了个例题练习

棋盘中的马
问题描述：
棋盘中有一个马，给出它的位置，它有一个目的地，请问它最少需要多少步才能走到它的目的地。马是走“日”字的

输入
•输入：第一行两个整数:$n,m，（n<=1000,m<=1000）$表示棋盘有$n$行$m$列。第一行第一列为$(1,1)$.
•第二行：$x_1$，$y_1$,表示马的位置。
•第三行：$x_2，y_2$,表示它的目的地。
•保证起始和终止位置都在棋盘内。
如果马不能到达目的地，输出$-1$.

输出
输出：马走到目的地所需的最少步数

样例输入

3 5
2 5
1 1

样例输出

3

策略分析：

这道题简单的bfs即可，双向bfs也可以，但是通过A*,以及A*+双向bfs来实现一下
其中的h(x)是通过计算欧式距离得到的，如果使用曼哈顿距离会出错，因为曼哈顿距离已经大于了实际的距离，因此使用欧式距离

A*

#include <iostream>
#include <cmath>
#include <queue>
#define MAXN 1005
using namespace std;
 
typedef struct node {
    int x, y;
    int f, g, h;
    node(){f = g = h = 0;}
    friend bool operator < (const node & a, const node &b);
}node;
inline bool operator < (const node & a, const node &b) {
    return a.f > b.f;
}
 
int n, m, dis[MAXN][MAXN];
int dx[8] = {-2, -2, -1, -1, 2, 2, 1, 1};
int dy[8] = {1, -1, -2, 2, -1, 1, -2, 2};
node start, en;
priority_queue <node> q; 
bool vst[MAXN][MAXN];
 
int Euclidean(int x, int y) {
    return (int)sqrt((x-en.x)*(x-en.x) + (y-en.y)*(y-en.y));
}
int Astar() {
    node now;
    q.push(start);
    dis[start.x][start.y] = 0;
    while(!q.empty()) {
        node t = q.top();
        q.pop();
        if(t.x == en.x && t.y == en.y) 
            return dis[t.x][t.y];
        for(int i = 0; i < 8; i++) {
            int nx = dx[i] + t.x;
            int ny = dy[i] + t.y;
            if(nx < 1 || nx > n || ny < 1 || ny > m) continue;
            if(!vst[nx][ny]) {
                vst[nx][ny] = 1;
                dis[nx][ny] = dis[t.x][t.y] + 1;
                now.x = nx, now.y = ny;
                now.h = Euclidean(nx, ny);
                now.g = t.g + 3;
                now.f = now.g + now.h;
                q.push(now);
            }
        }
    }
    return -1;
}
 
int main() {
    cin >> n >> m;
    cin >> start.x >> start.y >> en.x >> en.y; 
    int ans = Astar();
    cout << ans << "\n";
    return 0;
}

双向bfs+A*

#include <iostream>
#include <cmath>
#include <queue>
#define MAXN 1005
using namespace std;
 
typedef struct node {
    int x, y;
    int f, g, h;
    node(){};
    node(int _x,int _y){
        f = g = h = 0;
        x = _x; y = _y;
    }
    node(int _x, int _y, int _f, int _g, int _h) {
        x = _x; y = _y; 
        f = _f; g = _g; h = _h;
    }
    friend bool operator < (const node & a, const node &b);
}node;
inline bool operator < (const node & a, const node &b) {
    return a.f > b.f;
}
int n, m, dis[MAXN][MAXN];
int start_x, start_y, end_x, end_y;
int dx[8]={-2, -2, -1, -1, 2, 2, 1, 1};
int dy[8]={1, -1, -2, 2, -1, 1, -2, 2};
 
priority_queue <node> q1, q2; 
int vst[MAXN][MAXN];
int s_Euclidean(int x, int y) { 
    return (int)sqrt((x-end_x)*(x-end_x) + (y-end_y)*(y-end_y));
}
int e_Euclidean(int x, int y) { 
    return (int)sqrt((x-start_x)*(x-start_x) + (y-start_y)*(y-start_y));
}
int Astar() {
    int f0, g0, h0;
    node t;
    q1.push(node(start_x, start_y)), q2.push(node(end_x, end_y));
    dis[start_x][start_y] = 1, dis[end_x][end_y] = 1;
    vst[start_x][start_y] = 1, vst[end_x][end_y] = 2;
    while(!q1.empty() && !q2.empty()) {
        t = q1.top(), q1.pop(); 
        for(int i = 0; i < 8; i ++) {
            int nx = t.x + dx[i];
            int ny = t.y + dy[i];
            if(nx<1 || nx>n || ny<1 ||ny>m) continue;
            if(!dis[nx][ny]) {
                dis[nx][ny] = dis[t.x][t.y] + 1;
                vst[nx][ny] = 1; 
                h0 = s_Euclidean(nx, ny);
                g0 = t.g + 3; 
                f0 = h0 + g0; 
                q1.push(node(nx, ny, f0, g0, h0)); 
            }else if(vst[t.x][t.y] + vst[nx][ny] == 3) 
                return dis[t.x][t.y] + dis[nx][ny] - 1; 
        }
         
        t = q2.top(), q2.pop();
        for(int i = 0; i < 8; i ++) {
            int nx = t.x + dx[i];
            int ny = t.y + dy[i];
            if(nx<1 || nx>n || ny<1 ||ny>m) continue;
            if(!dis[nx][ny]) {
                dis[nx][ny] = dis[t.x][t.y] + 1;
                vst[nx][ny] = 2;
                h0 = e_Euclidean(nx, ny);
                g0 = t.g + 3;
                f0 = h0 + g0;
                q2.push(node(nx, ny, f0, g0, h0));
            }else if(vst[t.x][t.y] + vst[nx][ny] == 3)
                return dis[t.x][t.y] + dis[nx][ny] - 1;
        }
    }
    return -1;
}
 
int main() {
    cin >> n >> m;
    cin >> start_x >> start_y >> end_x >> end_y; 
    int ans = Astar();
    cout << ans << "\n";
    return 0;
}

最后贴一个：可视化搜索算法路径