排序算法整理(图文)
**
排序算法
**
排序分两类:
内部排序:将需要处理的数据都加载在内部存储器(内存)中进行。
外部排序:数据量过大无法全部加载到内存当中,需要借助外部存储进行排序!
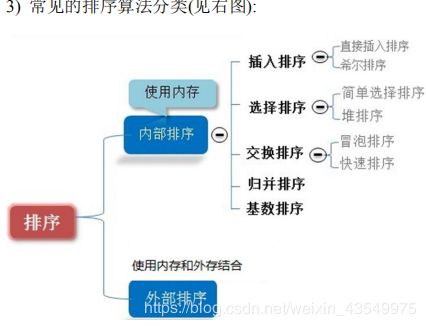
常见排序算法分类
- 冒泡排序(O(n^2))
基本思想:依次比较相连元素的值,若发现逆序则交换。
优化:因为排序的过程中,各元素不断接近自己的位置,如果一趟比较下来没有进行过交换,就说明序列有序,因此要在排序过程中设置一个标志flag判断元素是否进行过交换。从而减少不必要的比较。(这里说的优化,可以在冒泡排序写好后,在进行)
- 选择排序(O(O^2))
基本思想:将当中最小的元素与第一个元素位置交换,后面的依次执行。
分析图:
- 插入排序(O(n^2))
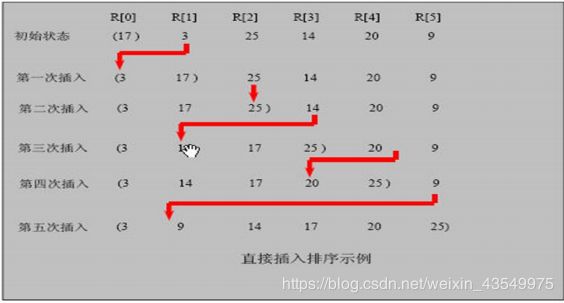
基本思想:将n个待排序的元素看成为一个有序表和一个无序表,开始有序表当中有一个元素,无序表当中有n-1个元素,下次执行将无序表当中取出一个元素与有序表当中元素进行比较,插入到有序表当中使其有序,重复执行该步骤。最后形成有序序列!
思路图:
- 希尔排序(O(nlogn))
基本思想:希尔排序是把记录按下标的一定增量分组,对每组使用直接插入排序算法排序;随着增量逐渐减少,每组包含的关键词越来越多,当增量减至1时,整个文件恰被分成一组,算法便终止。
希尔排序示意图:
- 快速排序
基本思想:通过一趟排序将要排序的数据分割成独立的两部分,其中一部分的所有数据都比另外一部分的所有数据都要小,然后再按此方法对这两部分数据分别进行快速排序,整个排序过程可以递归进行,以此达到整个数据变成有序序列。
示意图: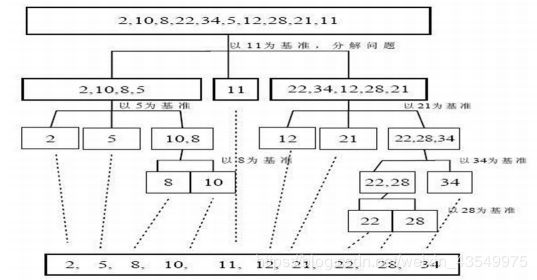

- 归并排序(O(nlogn))
基本思想:归并排序(MERGE-SORT)是利用归并的思想实现的排序方法,该算法采用经典的分治(divide-and-conquer)策略(分治法将问题分(divide)成一些小的问题然后递归求解,而治(conquer)的阶段则将分的阶段得到的各答案"修补"在一起,即分而治之)。
示意图-----1:
- 基数排序(O(nlogn))
基数排序(桶排序)介绍:
1)基数排序(radix sort)属于“分配式排序" (distribution sort) ,又称“桶子法” (bucket sort)或bin sort, 厨名思义,它是通过键值的各个位的值,将要排序的元素分配至某些“桶”中,达到排序的作用
2)基数排序法是属于稳定性的排序,基数排序法的是效率高的稳定性排序法
3)基数排序(Radix Sort)是桶排序的扩展
4)基数排序是1887年赫尔曼·何乐礼发明的。它是这样实现的:将整数按位数切割成不同的数字,然后按每个位数分别比较。
基本思想:将所有待比较数值统一为同样的数位长度,数位较短的数前面补零。然后,从最低位开始,依次进行一次排序这样从最低位排序一直到最高位排序完成以后,数列就变成一个有序序列。
图文说明:

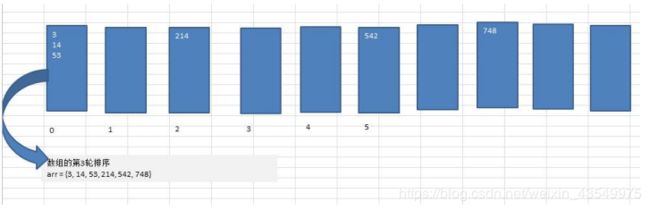
- 堆排序O(nlogn)
基本介绍:
堆排序是利用堆这种数据结构而设计的一种排序算法,堆排序是一种选择排序,它的最坏,最好,平均时间复杂度均为O(nlogn),它也是不稳定排序。
堆是具有以下性质的完全二叉树:每个结点的值都大于或等于其左右孩子结点的值,称为大顶堆,注意:没有要求结点的左孩子的值和右孩子的值的大小关系。
每个结点的值都小于或等于其左右孩子结点的值,称为小顶堆
大顶堆举例说明

小顶堆举例说明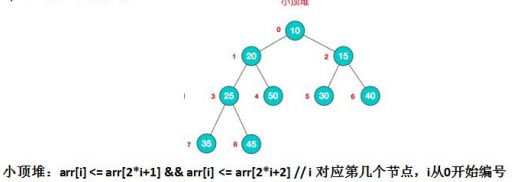
基本思想:
将待排序序列构造成一个大顶堆
此时,整个序列的最大值就是堆顶的根节点。
将其与末尾元素进行交换,此时末尾就为最大值。
然后将剩余n-1个元素重新构造成一个堆,这样会得到n个元素的次小值。如此反复执行,便能得到一个有序序列了。
可以看到在构建大顶堆的过程中,元素的个数逐渐减少,最后就得到一个有序序列了.
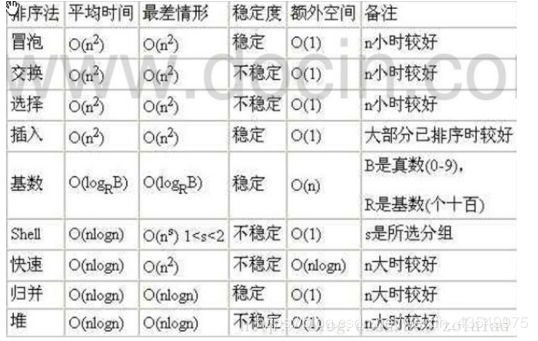
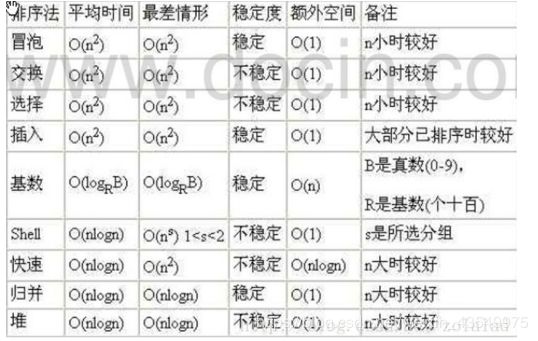
**排序算法 时-空 总结 **