python金融大数据分析笔记----第十章 推断统计1

第十章 推断统计

10.1 随机数
10.2 模拟
10.1.numpy.random生成随机数

import numpy.random as random
import matplotlib.pyplot as plt

# rand 函数返回开区间［O, 1)内的随机数,随机数的个数由参数指定
random.rand(10)#一维数组：10个
# array([0.11272845, 0.18209162, 0.04968643, 0.65770701, 0.21296395,
#       0.67249432, 0.45957752, 0.49175379, 0.53468779, 0.96999022])

random.rand(5, 5)#二维数组：5x5
# array([[ 0.95942423,  0.91671855,  0.33619313,  0.37931534,  0.59388659],
#        [ 0.84503838,  0.92572621,  0.57089753,  0.84832724,  0.6923007 ],
#        [ 0.0257402 ,  0.73027026,  0.07831274,  0.85126426,  0.43927961],
#        [ 0.31733426,  0.0367936 ,  0.26154412,  0.68299204,  0.06117947],
#        [ 0.3355343 ,  0.72317741,  0.95397264,  0.91341195,  0.8424168 ]])

# 如果想生成区间［5, 10)内的随机数， 可以这样转换 rand 的返回值
a = 5.
b = 10.
random.rand(10) * (b - a) + a
# array([ 7.72031281,  9.49373699,  7.26951207,  5.08434385,  7.07330462,
#         5.5169059 ,  7.93266969,  9.59174389,  7.55476132,  9.07963314])

# 由于 NumPy 的广播特性， 这也适合于多维数组
random.rand(5, 5) * (b - a) + a
# array([[ 6.56262146,  6.58686089,  9.25527619,  7.36295298,  8.10034672],
#        [ 9.51719011,  8.79297476,  7.32629772,  8.85443737,  6.95337673],
#        [ 9.87850678,  8.87835651,  5.55394611,  9.09984161,  7.46512384],
#        [ 8.54888728,  8.34351926,  7.95810147,  6.20483389,  8.86515313],
#        [ 9.37562883,  5.81284007,  8.34719867,  6.14204529,  7.31620939]])

表10-1 简单随机数生成函数

函数	参数	描述
rand	d0,d1,…,dn	指定组成的随机数
rndn	d0,d1,…,dn	来自标准正态分布的一个（或者多个）样本
randint	low[, high, size]	从low （含）到high （不含）的随机整数
random_integers	low[, high, size］	low和nigh (含）之间的随机整数
random_sample	[ size]	半开区间［0.0, 1.0）内的随机浮点数
random	[ size]	半开区间［0.0, 1.0）内的随机浮点数
ranf	[ size]	半开区间 [0.0, 1.0）内的随机浮点数
sample	[ size]	半开区间［0.0, 1.0）内的随机浮点数
choice	a[, size, replace, p]	给定一维数组中的随机样本
bytes	length	随机字节

将下列函数np.random.rand（），np.random.randint(），np.random.sample(），np.random.choice(）可视化，得到2个连续分布图和2个离散分布图

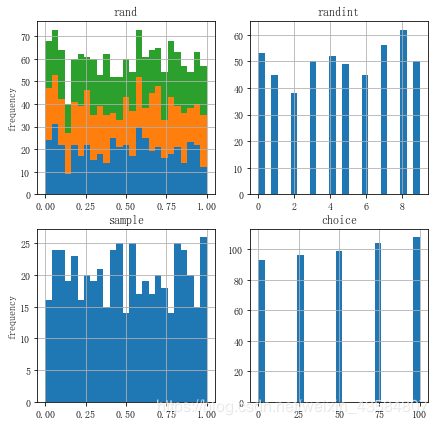
sample_size = 500
rn1 = random.rand(sample_size, 3)  #二维（500x3）
rn2 = random.randint(0, 10, sample_size) #获取[0,10)之间的500个随机数
rn3 = random.sample(size=sample_size) #获取[0.0,1.0)之间的500个随机数
a = [0, 25, 50, 75, 100]
rn4 = random.choice(a, size=sample_size) #随机获取a中的数值500个

fig, ((ax1, ax2), (ax3, ax4)) = plt.subplots(nrows=2, ncols=2, figsize=(7, 7))

ax1.hist(rn1, bins=25, stacked=True)
ax1.set_title('rand')
ax1.set_ylabel('frequency')
ax1.grid(True)

ax2.hist(rn2, bins=25)
ax2.set_title('randint')
ax2.grid(True)

ax3.hist(rn3, bins=25)
ax3.set_title('sample')
ax3.set_ylabel('frequency')
ax3.grid(True)

ax4.hist(rn4, bins=25)
ax4.set_title('choice')
ax4.grid(True)

表10-2 根据不同分布生成随机数的函数(np.random.函数(参数))

函数	参数	描述
beta	a, b[, size]	[0,1］区间上的β分布样本
binomial	n,p[, size]	二项分布样本
chisquare	df[, size]	卡方分布样本
dirichlet	alpha[, size]	狄利克雷分布样本
exponential	[ scale，size]	指数分布样本
f	dfnum, dfden[, size]	F分布样本
gamma	shape[, scale, size]	γ分布样本
geometic	p[, size]	集合分布样本
gumbel	[loc, scale, size]	刚贝尔分布样本
hypergeometric	ngood，nbad, nsample[,size]	超几何分布样本
laplace	[ loc, scale，size]	拉普拉斯分布或者双指数分布样本
Logistic	[ loc，scale, size]	逻羁分布样本
lognormalv	[ mean, sigma. size]	对数正态分布样本
logseries	p[,size]	对数序列分布样本
multinomial	n,pvals[, size]	多项分布样样本
multivaiate_normal	mean, cov[, size]	多变量正态分布样本
negative_binomial	n, p[, size]	负二项式分布样本
noncentral_chisquare	df, nonc[, size]	非中心卡方分布样本
noncentral_f	dfnum, dfden1 none[, size]	非中心F分布样本
normal	[ loc, scale, size]	正态（高斯）分布样本
pareto	a[, size]	特定组成的帕累托II或者洛马克思分布样本
poisson	[lam,size]	泊松分布
power	a[,size]	[0,1]区间内指数为正（a-1）的幂次分布样本
Rayleigh	[ scale,size]	瑞利分布样本
standard_cauchy	[ size]	标准柯西分布（模式0）样本
Standard_exponential	[ size]	标准指数分布样本
standard_gamma	shape[, size]	标准γ分布样本
standard_nonnal	[ size]	标准正态分布（均值为0，标准差为1）样本
standard_t	df[, size]	学生的t分布样本（自由度为df)
triangular	left, mode, right[, size]	三角分布样本
uniform	[ low, high, size]	均匀分布样本
vonmises	mu, kappa[, size］	冯·米塞斯分布样本
wald	mean, scale[, size]	瓦尔德（逆高斯）分布样本
weibull	a[, size]	戚布尔分布样本
zipf	a[, size]	齐夫分布样本

举例，
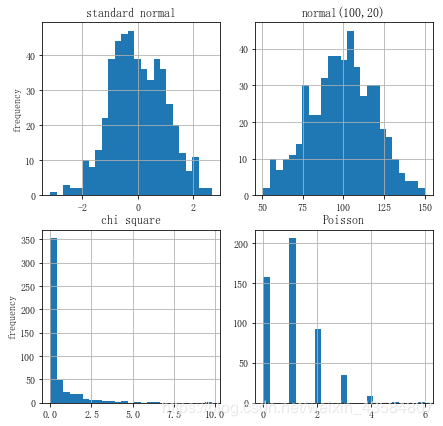
我们将可视化来 如下分布的随机数:

1. 均值为0 ，标准差为 1的标准正态分布
2. 均值为 100 标准差为 20 正态分布
3. 自由度为 0.5 卡方分布
4. $\lambda$值为1 的泊松分布

sample_size = 500
rn1 = random.standard_normal(sample_size)  # 均值为0, 标准差为1的标准正态分布
rn2 = random.normal(100, 20, sample_size)  # 均值为 100 ， 标准差为 20 的正态分布
rn3 = random.chisquare(df=0.5, size=sample_size)  # 自由度为 0.5 的卡方分布
rn4 = random.poisson(lam=1.0, size=sample_size)  # λ 值为 1 的泊松分布

下图展示了3个连续分布1个离散分布：

fig, ((ax1, ax2), (ax3, ax4)) = plt.subplots(nrows=2, ncols=2, figsize=(7, 7))
ax1.hist(rn1, bins=25)
ax1.set_title('standard normal')
ax1.set_ylabel('frequency')
ax1.grid(True)

ax2.hist(rn2, bins=25)
ax2.set_title('normal(100,20)')
ax2.grid(True)

ax3.hist(rn3, bins=25)
ax3.set_title('chi square')
ax3.set_ylabel('frequency')
ax3.grid(True)

ax4.hist(rn4, bins=25)
ax4.set_title('Poisson')
ax4.grid(True)

10.2. 模拟

• 在金融学中，两种模拟工作特别重要:
  • 随机变量
  • 随机过程
• 蒙特卡洛模拟（MCS）是金融学巾最重要的数值技术之 一(在重要性和使用广泛程度
  上也许没有"之一"）。 这主要是因为它是最灵活的数学表达式(如积分)求值方法，
  特别适合于金融衍生品的估值 。但是，这种灵活性的代价是相对高的计算负担，估算
  一·个值就可能需要数 十万次甚至数百万次复杂计算。

10.2.1 随机变量
通过蒙特卡洛方法估计欧式看涨期权的价值，考虑BMS(Black-Scholes-Merton）模拟，在这种模拟中期权潜在风险遵循几何布朗运动。

公式10-1 BMS(1973)到期指数水平)
$$S_T=S_{0}exp((r-\frac{1}{2}{\sigma }^2)T+\sigma \sqrt{T}z)$$

变量和参数的含义如下:

• $S_T$： $T$日的指数水平
• $S_0$：初始股票指数水平
• $r$：恒定元风险短期利字.
• $\sigma$：$S$的恒定波动率(=收益的标准差)
• $T$：到期时间
• $z$：标准正态分布随机变量

S0 = 100  #初始股票指数水平
r = 0.05  #无风险利率
sigma = 0.25 #固定波动率
T = 1. #1个月
I = 10000  #模拟次数

ST = S0 * np.exp((r - 0.5 * sigma ** 2) * T + sigma * np.sqrt(T) * np.random.standard_normal(I))

将其可视化

plt.hist(ST, bins=50)
plt.xlabel('index level')
plt.ylabel('frequency')
plt.grid(True)

( 通过 standard_normal ) 模拟的几何布朗运动

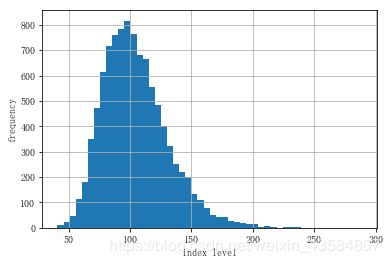
从图中可以看出，公式10-1定义的随机变量呈对数正态分布。因此 ， 我们还可以尝试使用 lognormal 函数直接得出随机变量值。在这种情况下，必须向函数提供均值和标准差：

ST2 = S0 * np.random.lognormal((r - 0.5 * sigma ** 2) * T, sigma * np.sqrt(T), size=I)
plt.hist(ST2, bins=50)
plt.xlabel('index level')
plt.ylabel('frequency')
plt.grid(True)

( 通过 lognormal ) 模拟的几何布朗运动

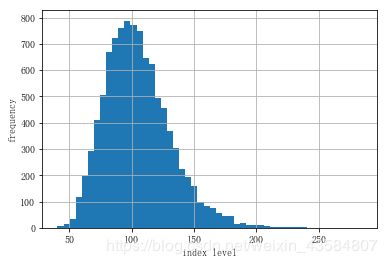
通过视觉检验，上面2个图看起来很相似，、
但是我们还是需要通过比较结果分布分统计矩更加严格地检验，对此，可使用 scipy.stats子库和下面定义的助手函数print_statistics 比较模拟结果的分布特性：

def print_statistics(a1, a2):
    """
    Print selected statistics
    """
    sta1 = scs.describe(a1)
    sta2 = scs.describe(a2)
    print('%14s %14s %14s' % ('statistic', 'data set 1', 'data set 2'))
    print(45 * '-')
    print('%14s %14.3f %14.3f' % ('size', sta1[0], sta2[0]))
    print('%14s %14.3f %14.3f' % ('min', sta1[1][0], sta2[1][0]))
    print('%14s %14.3f %14.3f' % ('max', sta1[1][1], sta2[1][1]))
    print('%14s %14.3f %14.3f' % ('mean', sta1[2], sta2[2]))
    print('%14s %14.3f %14.3f' % ('std', np.sqrt(sta1[3]), np.sqrt(sta2[3])))
    print('%14s %14.3f %14.3f' % ('skew', sta1[4], sta2[4]))
    print('%14s %14.3f %14.3f' % ('kurtosis', sta1[5], sta2[5]))

print_statistics(ST, ST2)

     statistic     data set 1     data set 2
---------------------------------------------
          size      10000.000      10000.000
           min         35.155         33.783
           max        292.218        257.247
          mean        105.119        104.748
           std         26.687         26.728
          skew          0.808          0.818
      kurtosis          1.392          1.252

显然，两个模拟结果的特性很类似， 差异主要是由于模拟中的所谓采样误差。在离散地模拟连续随机过程时会引人离散化误差， 但是由于模拟方法的特性，这种误差在此不起任何作用。

10.2.2 随机过程
粗略地讲， 随机过程是一个随机变量序列。在这个意义上， 我们应该预期， 在模拟一个过程时， 对一个随机变量的一序列重复模拟应该有某种类似之处。 这个结论大体上是正确的 ，但是随机数的选取一般不是独立的？而是依赖于前几次选取的结果。 不过，金融学中使用的随机过程通常表现出马尔科夫特性——主要的含义是：明天的过程值只依赖于今天的过程状态， 而不依赖其他任何 “历史” 状态． 甚至不依赖整个路径历史。 这种过程也被称做 “无记忆过程”。

10.2.2.1几何布朗运动
现在我们考虑Black-Scholes-Merton模型的动态形式，这种形式由公式10-2中的随机微分方程(SDE)描述。式中的$Z_t$ 是标准布朗运动，SDE 被称作几何布朗运动。$S_t$ 的值呈对数正态分布，（边际）收益$dS{t}_{/}{S}_t$呈正态分布。

公式10-2 Black-Scholes-Merton设置中的随机微分方程
$$d{S}_t=r{S}_t{d}_t+\sigma S_{t}d{Z}_t$$
公式10-2中的SDE可以由一个欧拉格式精确地离散化，下面公式10-3中介绍了一个这样的格式， 其中$\Delta t$是固定的离散化间隔， $z_t$ 是标准正态分布随机变量。

公式10-3 在Black-Scholes-Merton设置中动态模拟指数水平
$$S_t=S_{t-\Delta t}exp\left(\left(r-\frac{1}{2}{\sigma }^2\right)\Delta t+\sigma \sqrt{\Delta t}{Z}_t\right)$$

I = 10000
M = 50
dt = T / M
S = np.zeros((M + 1, I))  #产生以0为值的二维数组(51, 10000)
S[0] = S0

for t in range(1, M + 1):
    S[t] = S[t - 1] * np.exp((r - 0.5 * sigma ** 2) * dt + sigma * np.sqrt(dt) * np.random.standard_normal(I))

plt.hist(S[-1], bins=50)
plt.xlabel('index level')
plt.ylabel('frequency')
plt.grid(True)

到期日的模拟几何布朗运动

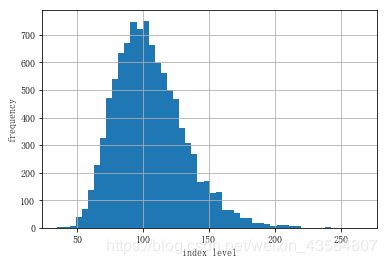
前4个统计矩和静态模拟方法得出的结果相当接近：

print_statistics(S[-1], ST2)

     statistic     data set 1     data set 2
---------------------------------------------
          size      10000.000      10000.000
           min         35.195         40.967
           max        266.059        263.658
          mean        105.545        105.192
           std         26.710         26.619
          skew          0.749          0.775
      kurtosis          0.973          1.111

下图为我们展示了前20条模拟路径：

plt.plot(S[:, :20], lw=1.5)
plt.xlabel('time')
plt.ylabel('index level')
plt.grid(True)

模拟几何布朗运动路径:

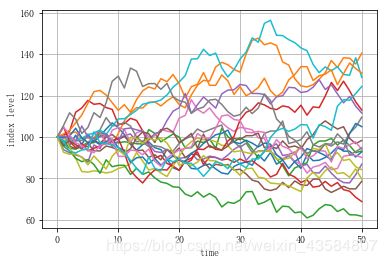
使用动态模拟方怯不仅可以像上图那样可视化路径，还可以估算美式/百慕大期权或者收益与路径相关的期权价值。 可以这么说， 你所得到的是全动态图像。

2.2.2 平方根扩散
另一类重要的金融过程是均值回归过程，用于建立短期利率或者波动性过程的模型。流行和广泛使用的模型之一是平方根扩散 公式提供了对应的SDE。
公式10-4 平方根扩散的随机微分方程
$$d{x}_t=k(\theta -x_t)dt+\sigma \sqrt{x_t}d{Z}_t$$式中，
$x_t$：日期 t 的过程水平
$k$ ： 均值回归因子
$\theta$ ：长期过程均值
$\sigma$ ：恒定波动率参数
$Z$ ：标准布朗运动
其中，$x_t$的值呈卡方分布。但是，许多金融模型可以使用正态分布进行离散化和近似计算（即所谓的欧拉离散化格式）。虽然欧拉格式对几何布朗运动很准确 ，但是对于大部分其他随机过程则会产生偏差。即使有精确的格式，因为数值化或者计算的原因，使欧拉格式可能最合适。
定义$s\equiv t-\Delta t$和$x^{+}\equiv max(x,0)$，公式10-5提出了一种欧拉格式。这种特殊格式在文献中通常称作完全截断。
公式10-5 平方根扩散的欧拉离散化
$${\tilde{x}}_t={\tilde{x}}_s+k(\theta -{\tilde{x}}_s^{+})\Delta t+\sigma \sqrt{{\tilde{x}}_s^{+}}\sqrt{\Delta t{z}_t}$$$$x_t={\tilde{x}}_t^{+}$$
我们用可以表示短期利率模型的值参数化后续模拟所用的模型：
平方根扩散有方便和实际的特性——$x_t$ 的值严格为正。用欧拉格式离散化时，负值无法排除。这就是人们处理的总是原始模拟过程整数版本的原因。因此在模拟代码中，需要两个ndarray对象，而不是1个：

x0 = 0.05
kappa = 3.0
theta = 0.02
sigma = 0.1
I = 10000
M = 50
dt = T / M

def srd_euler():
    xh = np.zeros((M + 1, I))
    x1 = np.zeros_like(xh)
    xh[0] = x0
    x1[0] = x0
    for t in range(1, M + 1):
        xh[t] = (xh[t - 1]
                 + kappa * (theta - np.maximum(xh[t - 1], 0)) * dt
                 + sigma * np.sqrt(np.maximum(xh[t - 1], 0)) * np.sqrt(dt)
                 * np.random.standard_normal(I))
    x1 = np.maximum(xh, 0)
    return x1

x1 = srd_euler()

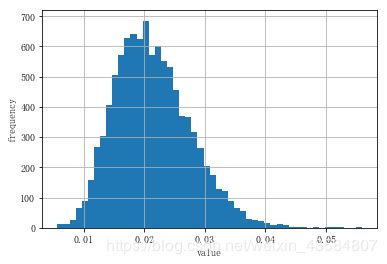
plt.hist(x1[-1], bins=50)
plt.xlabel('value')
plt.ylabel('frequency')
plt.grid(True)

到期日的模拟平方根扩散（欧拉格式）

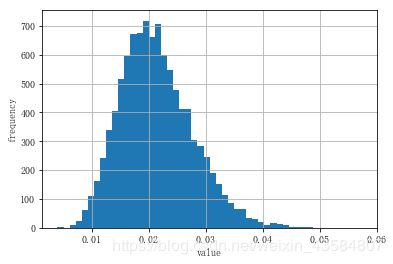
关于np.maximum()函数，可参考：这篇文章：np.max()， np.maximum()， np.argmax()
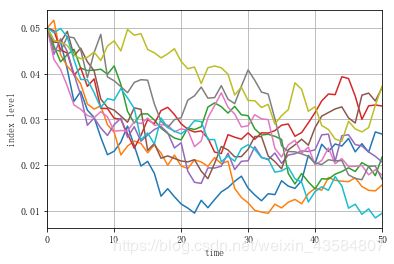
下图展示了前 10 条模拟路径，说明得出的平均偏离值为负值（因为 $x0>\theta$）并收敛于 $\theta =0.02$。

plt.plot(x1[:, :10], lw=1.5)
plt.xlabel('time')
plt.ylabel('index level')
plt.xlim(0,50)
plt.grid(True)

现在我们寻求更精确的结果。下面公式提出了基于自由度 $df=\frac{4{\theta }_{\kappa }}{{\sigma }^2}$，非中心参数 $nc=\frac{4\kappa e^{-\kappa \Delta t}}{{\sigma }^2(1-e^{-\kappa \Delta t})}{x}_s$的卡方分布${\chi }_d^{{}^{\prime }2}$平方根扩散的精准离散化格式。

公式10-6 平方根扩散的精确离散化
$$x_t=\frac{{\sigma }^2(1-e^{-k\Delta t})}{4k}{\chi }_d^{{}^{\prime }2}\left(\frac{4k{e}^{-k\Delta t}}{{\sigma }^2(1-e^{-k\Delta t})}{x}_s\right)$$
以下是平方根扩散的精确离散化的python实现：

def srd_exact():
    x2 = np.zeros((M + 1, I))
    x2[0] = x0
    for t in range(1, M + 1):
        df = 4 * theta * kappa / sigma ** 2
        c = (sigma ** 2 * (1 - np.exp(-kappa * dt))) / (4 * kappa)
        nc = np.exp(-kappa * dt) / c * x2[t - 1]
        x2[t] = c * np.random.noncentral_chisquare(df, nc, size=I)
    return x2

x2 = srd_euler()

plt.hist(x2[-1], bins=50)
plt.xlabel('value')
plt.ylabel('frequency')
plt.grid(True)

到期日的模拟平方根扩散（精确格式）

plt.plot(x2[:, :10], lw=1.5)
plt.xlabel('time')
plt.ylabel('index level')
plt.grid(True)

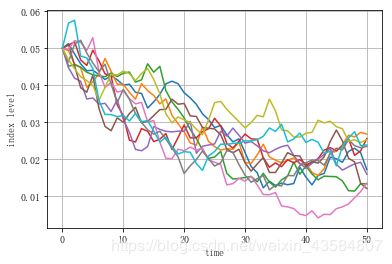
上图获得10调模拟路径，同样呈现负的平均漂移,收敛于$\theta$
比较不同方法中的主要统计数字可以看出， 偏置欧拉格式确实很好地表现出理想的统计属性：

#x1：平方根扩散的欧拉离散化
#x2: 平方根扩散的精确离散化
print_statistics(x1[-1], x2[-1])

     statistic     data set 1     data set 2
---------------------------------------------
          size      10000.000      10000.000
           min          0.004          0.006
           max          0.057          0.056
          mean          0.021          0.021
           std          0.006          0.006
          skew          0.577          0.541
      kurtosis          0.515          0.389

但在执行速度方面可以观察到重大的差异。这是因为从非中心卡方分布中采样的计算要求高于标准正态分布的采样。为了说明这一点， 我们考虑更大的模拟路径数量：

I=250000
%time x1=srd_euler()
# Wall time: 1.73 s

%time x2=srd_exact()
# Wall time: 2.05 s

精确格式大约需要花费2倍的时间，而结果实际上和欧拉格式大致相同;
如下，当$I=250000$时，

print_statistics(x1[-1], x2[-1])

     statistic     data set 1     data set 2
---------------------------------------------
          size     250000.000     250000.000
           min          0.004          0.004
           max          0.065          0.063
          mean          0.021          0.022
           std          0.006          0.006
          skew          0.560          0.577
      kurtosis          0.475          0.514

2.2.3 随机波动率
Black-Scholes-Meron模型中重要的简化假设之一是恒定波动率。
但是， 波动率一般来说既不是恒定的、也不具确定性， 而是随机的。
因此，20世纪90年代初金融模型的重大进步之一是所谓随机波动率模型的推出。
这一类别中最为流行的模型之一是Heston ( 1993 ）模型：
公式10-7 Heston随机流动率模型的随机徽分方程
$$d{S}_t=r{S}_{t}dt+\sqrt{v_t}{S}_{t}d{Z}_t^1$$$$d{v}_t=k_v({\theta }_v-v_t)dt+{\sigma }_v\sqrt{v_t}d{Z}_t^2$$$$d{Z}_t^{1}d{Z}_t^2=\rho$$
单一变量和参数的均值现在很容易从几何布朗运动和平方根扩散的讨论中得出。另外，
参数 $\rho$ 代表两个标准布朗运动$Z_t^1$ ，$Z_t^2$之间的瞬时相关性。这使我们可以解释一个典型事实——杠杆效应， 该效应本质上指的是波动性在困难时期（衰退市场）中上升， 而在牛市（上升市场）时下降。

S0 = 100.
r = 0.05
v0 = 0.1
kappa = 3.0
theta = 0.25
sigma = 0.1
rho = 0.6 
T = 1.0

import numpy as np
# 为了说明两个随机过程之间的相关性，我们需要确定相关矩阵的柯列斯基分解：
corr_mat = np.zeros((2, 2))
corr_mat[0, :] = [1.0, rho]
corr_mat[1, :] = [rho, 1.0]
cho_mat = np.linalg.cholesky(corr_mat)
print(cho_mat)
# array([[ 1. ,  0. ],
#        [ 0.6,  0.8]])

# =============================================================================
# 关于np.linalg.cholesky(corr_mat)
'''
corr_mat
Out[65]: 
array([[1. , 0.6],
       [0.6, 1. ]])

cho_mat
Out[66]: 
array([[1. , 0. ],
       [0.6, 0.8]])

cho_mat[0][0]**2 + cho_mat[0][1]**2
Out[69]: 1.0

cho_mat[1][0]**2 + cho_mat[1][1]**2
Out[70]: 1.0
'''
# =============================================================================

# 在开始模拟随机过程之前， 我们为两个过程生成整组随机数， 指数过程使用第0组，波动性过程使用第1组：
M = 50
I = 10000
ran_num = np.random.standard_normal((2, M + 1, I))
# 对于以平方根扩散过程类型建模的波动性过程， 我们使用欧拉格式， 考虑相关性参数：
dt = T / M
v = np.zeros_like(ran_num[0])
vh = np.zeros_like(v)
v[0] = v0
vh[0] = v0
for t in range(1, M + 1):
    ran = np.dot(cho_mat, ran_num[:, t, :])
    vh[t] = (vh[t - 1] + kappa * (theta - np.maximum(vh[t - 1], 0)) * dt
             + sigma * np.sqrt(np.maximum(vh[t - 1], 0)) * np.sqrt(dt)
             * ran[1])
    v = np.maximum(vh, 0)

# 对于指数水平过程, 我们也考虑相关性，使用几何布朗运动的精确欧拉格式：
S = np.zeros_like(ran_num[0])
S[0] = S0
for t in range(1, M + 1):
    ran = np.dot(cho_mat, ran_num[:, t, :])
    S[t] = S[t - 1] * np.exp((r - 0.5 * v[t]) * dt +
                             np.sqrt(v[t]) * ran[0] * np.sqrt(dt))

'''
这说明了平方根扩散中使用欧拉格式的另一项优势：
相关性很容易一致性地处理， 因为我们只提取标准正态随机数。 没有一种棍合方法（对指数使用欧拉格式， 对波动性过程使用基于非中心卡方分布的精确方法）能够实现相同的效果。
'''
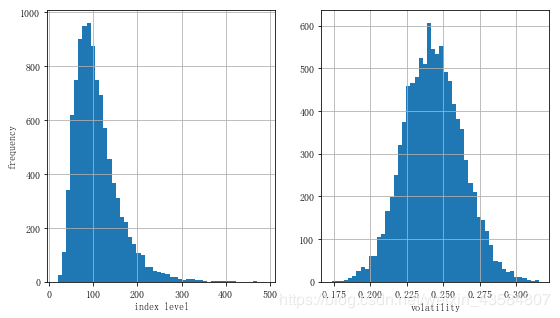
# 用直方图展了指数水平过程和波动性过程的模拟结果
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(9, 5))
ax1.hist(S[-1], bins=50)
ax1.set_xlabel('index level')
ax1.set_ylabel('frequency')
ax1.grid(True)
ax2.hist(v[-1], bins=50)
ax2.set_xlabel('volatility')
ax2.grid(True)

#模拟随机波动率模型路径
fig, (ax1, ax2) = plt.subplots(2,1,sharex=True, figsize=(7, 6))
ax1.plot(S[:,:10],lw=1.5)
ax1.set_ylabel('index level')
ax1.grid(True)
ax2.plot(v[:,:10],lw=1.5)
ax2.set_xlabel('time')
ax2.set_ylabel('volatility')
ax2.grid(True)

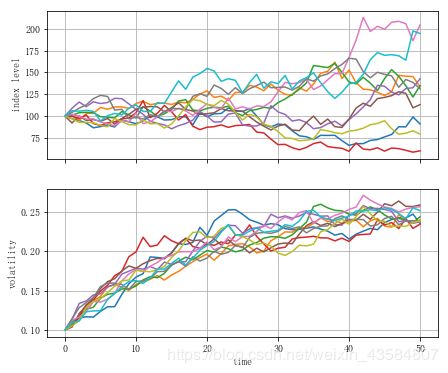
对每个过程的前10条模拟路径的检查表明， 波动性过程的平均漂移值为正数， 和预期的一样收敛于${\theta }_v=0.25$
最后， 我们简短地看着两个数据集最后一个时间点的统计数字，该时点显示指数水平过程有一个相当高的最大值。实际上，在其他条件不变的情况下，这个最大值远大于固定披动率下几何布朗运动所能达到的最大值：

print_statistics(S[-1], v[-1])
     statistic     data set 1     data set 2
---------------------------------------------
          size      10000.000      10000.000
           min         18.561          0.173
           max        489.802          0.316
          mean        107.874          0.243
           std         50.926          0.020
          skew          1.611          0.119
      kurtosis          4.770          0.011

2.2.3 跳跃扩散
随机波动率和杠杆效应是在许多市场上都能发现的典型（经验主义）事实。另一种典型的经验主义事实是资产价格和波动率的跳跃。1976年， Meron发布了他的跳跃扩散模型， 模型的一个部分以对数正态分布生成跳跃， 改进了Black-Scholes-Merton设置。
风险中立SDE如下：
公式10-8 Meron跳跃扩散模型的随分方程
$$d{S}_t=(r-r_J)S_{t}dt+\sigma S_{t}d{Z}_t+J_t{S}_{t}d{N}_t$$