循环队列的顺序存储
循环队列的顺序存储
队列是一种操作受限(先进先出)的线性表,今天我们来实现队列的顺序存储结构。
在队列的顺序存储中,用一组地址连续的存储单元依次存放队头到对尾的数据元素,即为顺序队列。
定义一个静态数组,每次尾插元素,即构成队列。
第一种方法
设置一个指针size作为计数(记录有效元素的个数)
(1).入队列,时间复杂度O(1)。
(2).出队列,每次出第一个元素,将第一个元素之后的元素依次向前搬移一个位置,时间复杂度为O(N);
优点:没有造成假溢出。
缺点:出队列的时间复杂度太高。
第二种方法
设置两个指针,分别为front和rear,front指向队头元素,rear指向队尾元素的下一个位置.
(1).入队列,时间复杂度O(1)。
(2).出队列,让队头指针front向后移动一个位置,时间复杂度为O(1).
缺点:容易造成假溢出。
优点:出队列时间复杂度为O(1).
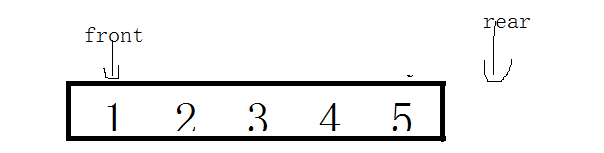
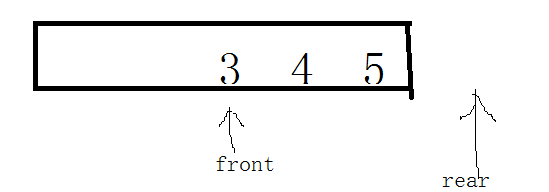
假溢出:前面的两个空间没有得到利用。队列的存储空间没有真正被占满。
解决假溢出(循环队列)
为了解决假溢出现象,使队列的存储空间得到充分利用,就是将数组看成一个假象的环形结构。
1.环形队列如何区分空和满。
(1).可以少用一个空间。
(q->rear+1)%Maxsize == q->front 则队列满。
q->rear==q->front 则队列空。
队列长度为 ((q->rear-q->front)+Maxsize)%Maxsize;
代码实现:
#include
#include
#include
typedef int QDataType;
typedef struct Queue
{
QDataType arr[5];
int front;
int rear;
}Queue;
void InitQueue(Queue* q);
void DestroyQueue(Queue* q);
void PushQueue(Queue* q, QDataType data);
void PopQueue(Queue* q);
QDataType front(Queue* q);
QDataType rear(Queue* q);
int empty(Queue* q);
int length(Queue* q);
void Print(Queue* q);
void Print(Queue* q)
{
assert(q);
int i = 0;
for (i = q->front; i !=q->rear;)
{
printf("%d ", q->arr[i]);
i = (i + 1) % 5;
}
printf("\n");
}
void InitQueue(Queue* q)
{
assert(q);
q->front = q->rear = 0;
}
void DestroyQueue(Queue* q)
{
assert(q);
if (q->arr)
{
q->front = q->rear = 0;
}
}
void PushQueue(Queue* q, QDataType data)
{
assert(q);
if ((q->rear+1)%5==q->front)
return;
q->arr[q->rear++] = data;
if (q->rear == 5)
{
q->rear = 0;
}
}
void PopQueue(Queue* q)
{
assert(q);
if (q->front==q->rear)
return;
q->front++;
if (q->front == 5)
{
q->front = 0;
}
}
QDataType front(Queue* q)
{
assert(q);
return q->arr[q->front];
}
QDataType rear(Queue* q)
{
assert(q);
if (q->rear == 0)
return q->arr[5 - 1];
else
return q->arr[q->rear - 1];
}
int empty(Queue* q)
{
assert(q);
return (q->rear==q->front);
}
int length(Queue* q)
{
assert(q);
return (((q->rear) - (q->front)) + 5) % 5;
}
测试:
int main()
{
Queue q;
InitQueue(&q);
PushQueue(&q, 1);
PushQueue(&q, 2);
PushQueue(&q, 3);
PushQueue(&q, 4);
PushQueue(&q, 5);
PushQueue(&q, 5);
PushQueue(&q, 5);
printf("%d %d\n", empty(&q), length(&q));
printf("%d %d\n", front(&q), rear(&q));
Print(&q);
PopQueue(&q);
PopQueue(&q);
PushQueue(&q, 6);
PushQueue(&q, 7);
PushQueue(&q, 8);
printf("%d %d\n", empty(&q), length(&q));
printf("%d %d\n", front(&q), rear(&q));
Print(&q);
DestroyQueue(&q);
system("pause");
return 0;
}
(2)给一个标记flag
q->rear == q->front && flag == 0 队列为空
q->rear == q->front &&flag==1 队列为满
代码实现:
#include
#include
#include
typedef int QDataType;
typedef struct Queue
{
QDataType arr[5];
int front;
int rear;
int flag;
}Queue;
void InitQueue(Queue* q);
void DestroyQueue(Queue* q);
void PushQueue(Queue* q, QDataType data);
void PopQueue(Queue* q);
QDataType front(Queue* q);
QDataType rear(Queue* q);
int empty(Queue* q);
int length(Queue* q);
void Print(Queue* q);
void Print(Queue* q)
{
assert(q);
int i = 0;
int flag = 0;
for (i = q->front; i !=q->rear||flag==0; i++)
{
printf("%d ", q->arr[i]);
if (i == 4)
i = -1;
flag = 1;
}
printf("\n");
}
void InitQueue(Queue* q)
{
assert(q);
q->front = q->rear = 0;
q->flag = 0;
}
void DestroyQueue(Queue* q)
{
assert(q);
if (q->arr)
{
q->front = q->rear = 0;
q->flag = 0;
}
}
void PushQueue(Queue* q, QDataType data)
{
assert(q);
if (q->flag ==1&&q->front==q->rear)
return;
q->arr[q->rear++] = data;
if (q->rear == 5)
{
q->rear = 0;
if (q->front == q->rear)
q->flag = 1;
}
}
void PopQueue(Queue* q)
{
assert(q);
if (q->flag ==0&&q->front==q->rear)
return;
q->front++;
if (q->front == 5)
{
q->front = 0;
if (q->front == q->rear)
q->flag = 0;
}
}
QDataType front(Queue* q)
{
assert(q);
return q->arr[q->front];
}
QDataType rear(Queue* q)
{
assert(q);
if (q->rear == 0)
return q->arr[5 - 1];
else
return q->arr[q->rear - 1];
}
int empty(Queue* q)
{
assert(q);
return (q->flag ==0)&&(q->rear==q->front);
}
int length(Queue* q)
{
assert(q);
if (q->flag == 1 && q->front == q->rear)
return 5;
else
return (((q->rear) - (q->front)) + 5) % 5;
}
(3)给一个计数器count(记录队列中元素的个数)
队空 count == 0;
堆满 count==Maxsize;
代码实现:
#include
#include
#include
typedef int QDataType;
typedef struct Queue
{
QDataType arr[5];
int front;
int rear;
int count;
}Queue;
void InitQueue(Queue* q);
void DestroyQueue(Queue* q);
void PushQueue(Queue* q, QDataType data);
void PopQueue(Queue* q);
QDataType front(Queue* q);
QDataType rear(Queue* q);
int empty(Queue* q);
int length(Queue* q);
void Print(Queue* q);
void InitQueue(Queue* q)
{
assert(q);
q->front = q->rear = 0;
q->count = 0;
}
void DestroyQueue(Queue* q)
{
assert(q);
if (q->arr)
{
q->front = q->rear = 0;
q->count = 0;
}
}
void PushQueue(Queue* q, QDataType data)
{
assert(q);
if (q->count==5)
return;
q->arr[q->rear++] = data;
if (q->rear == 5)
{
q->rear = 0;
}
q->count++;
}
void PopQueue(Queue* q)
{
assert(q);
if (q->count==0)
return;
q->front++;
if (q->front == 5)
{
q->front = 0;
}
q->count--;
}
QDataType front(Queue* q)
{
assert(q);
return q->arr[q->front];
}
QDataType rear(Queue* q)
{
assert(q);
if (q->rear == 0)
return q->arr[5 - 1];
else
return q->arr[q->rear - 1];
}
int empty(Queue* q)
{
assert(q);
return q->count == 0;
}
int length(Queue* q)
{
assert(q);
return q->count;
}
void Print(Queue* q)
{
assert(q);
int i = 0;
int flag = 0;
for (i = q->front; i !=q->rear||flag==0; i++)
{
printf("%d ", q->arr[i]);
if (i == 4)
i = -1;
flag = 1;
}
printf("\n");
}
测试
int main()
{
Queue q;
InitQueue(&q);
PushQueue(&q, 1);
PushQueue(&q, 2);
PushQueue(&q, 3);
PushQueue(&q, 4);
PushQueue(&q, 5);
PushQueue(&q, 5);
PushQueue(&q, 5);
printf("%d %d\n", empty(&q), length(&q));
printf("%d %d\n", front(&q), rear(&q));
Print(&q);
PopQueue(&q);
PopQueue(&q);
PushQueue(&q, 6);
PushQueue(&q, 7);
PushQueue(&q, 8);
printf("%d %d\n", empty(&q), length(&q));
printf("%d %d\n", front(&q), rear(&q));
Print(&q);
DestroyQueue(&q);
system("pause");
return 0;
}