门控图神经网络及PyTorch实现
门控图神经网络及PyTorch实现
- 前言
- GNN预备知识
- 面对一大串公式不得不说的定理
- *巴拿赫不动点定理*
- GNN信息传播特点——可达性任务展示
- 具体实现
- *隐藏状态的计算*
- *GNN网络框架*
- *算法Forward and Backward*
- 从GNN到GGNN
- GNN的局限
- GGNN的改变
- 门控图神经网络
- 传播过程
- 大致算法步骤
- 门控图神经网络PyTorch模型代码
- model.py
- *GatedPropagation类*
- *GraphFeature类*
- 创建邻接矩阵——将三元组变为邻接矩阵
- 以task-18为例
- data.py
- *get_data_types函数*
- *load_graph_from_file函数*
- *data_convert函数*
- get_loader and BABI class
- main.py
- train.py
前言
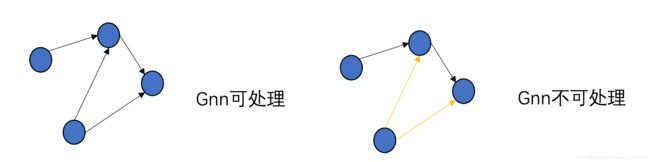
图神经网络与其他神经网络的最大不同点在于一般的神经网络处理规则的是规则且排列整齐的数据类型,如图像(网格数据),和文本(序列数据),而图神经网络的出现正是为了处理排列相对不整齐,对于数据中的某个点很难找到他的邻居节点,并且邻居节点数量是不固定的数据。下图中左图是CNN拿手的图,右图是GNN拿手的图。
GNN预备知识
面对一大串公式不得不说的定理
巴拿赫不动点定理
我们有一堆由两个自变量构成的数据,这堆数据在坐标轴上画出可以构成一个平面区域,我们找到一个方式F能改变平面区域内的点的位置,并且使得这个区域缩小(压缩映射),从图中我们可以看出x,y两个点经过一个F的作用后距离缩小了,假如我们以同样的方式再次作用在缩小后的平面区域,显然这个区域会再次缩小,经过无数次作用,整个区域就会无限接近于一个点。

我们把这个定理形象的用于射靶子,刚玩打靶,你可能命中的区域非常大,通过一段时间的训练学习修改自己的方法,命中区域开始缩小并且以靶心为目标靠近,通过长年累月不断的改进学习,最终可达到精确击中靶心。

GNN训练过程也是一个不断寻找精确的能使得大量信息融合最后能用一个矩阵或者向量表示出来的过程。
GNN信息传播特点——可达性任务展示
这虽然不是单靠GNN就能实现的例子,但能反应出GNN利用边传播信息的特点

假设我们有这样一个图,很显然我们一眼可以看出节点1可以通过1 -> 2 , 2 -> 4 ,来到达节点4,但是计算机需要学习怎么推理从节点1能否到达节点4。我们首先要把这个图转化成能输入计算机的数据,比如说把节点设为一个向量,把节点间的关系用矩阵来表示:

我们把上面的节点整合成一个向量:[1,0,0,0,0,0,0,1]。
再把边用矩阵表示出来:

最后整张图如下所示

最终我们发现两次运算就可以推理出能否到达。从过程可以看出,每一次的结果都是由某条边的存在而产生,信息通过边来传递。

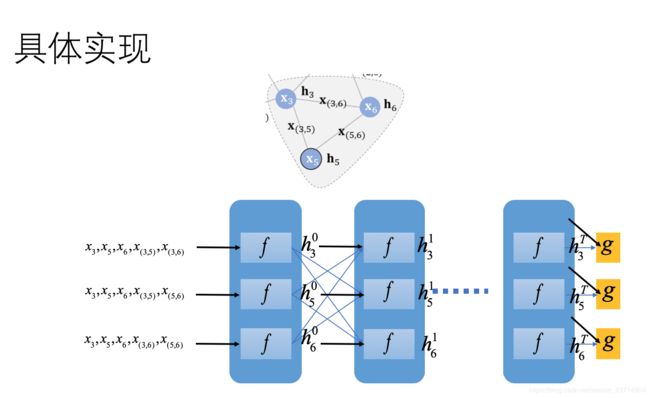
具体实现
隐藏状态的计算
首先我们需要将某个节点的周围信息融合成一个向量表示,我们把这个信息定义为隐藏状态,从式子中我们就可以发现节点特征x和隐藏状态h的不同点,节点特征x仅包含该节点的信息,而隐藏状态包含节点周围的全部信息。 GNN的目标就是将隐藏信息计算精确,根据巴拿赫不动点定理,只要我们找到一个能够使得我们缩小打靶范围,打中靶子更加精确的方法(也就是我们的f函数),我们就可以将节点周围的全部信息浓缩在h内,在这之前,我们先要弄清要把哪些数据输入f函数。我们需要输入表示节点的特征、表示边的特征、表示邻居节点隐藏信息的特征,表示邻居节点的特征。

最终的隐藏信息是我们不能利用的,我们要利用一个函数g使得隐藏信息能够与正确结果比较并计算误差,这个函数可以是全连接网络。我们开始综合所有节点构建整个框架。
GNN网络框架
以上图三个节点为例,一开始我们要初始化节点的隐藏信息,将要输入的信息输入f函数,得到x3的隐藏信息h3,同理可得到h5,h6,再利用上面的公式将输入信息与隐藏信息结合,再输入到f函数内,直到h3,h5,h6不再有很大的变化,即收敛,也就是成为了不动点,利用网络g输出,与标签比较,计算损失,反向传播,不断更新f的参数,最终损失函数也达到最小值。这个时候就会问,把前面计算隐藏信息的步骤结合起来将计算用一个图来表示不就是下面画的全连接网络吗,其实和全连接网络还是有区别的。
- 全连接网络的隐藏层数目是固定的,GNN 隐藏层基于不动点定理必须迭代至收敛。
- 全连接网络前向传播一次后就可反向传播,GNN需要全图收敛才能反向传播。
这两点会在后面的算法中体现出来
算法Forward and Backward
- 从main函数中可以看出必须先进行一次forward收敛后再backward更新参数。
- 从forward函数可以看出迭代算法结束条件是隐藏状态变化量小于一个极小值,趋于不动点。
- 从backward函数。。。
从GNN到GGNN
GNN的局限
基于不动点理论的图神经网络GNN,它的核心观点是通过节点信息的传播使整张图达到收敛,在其基础上才能再进行预测。不动点作为GNN的核心思想,同样局限了GNN更广泛的使用。GNN存在两个突出问题:
- GNN只将边作为一种传播手段,并未区分不同边的功能: 虽然我们可以在构造阶段将输入进f的x(u,v)即变得信息赋予不同的特征,但相比于其他的输入,边对最终的隐藏状态结果的影响实在有限。
- GNN没有为设置独立可学习的参数 也就意味着无法通过模型学习到边的某些特性。
- 将GNN运用于真实图会存在较多信息共享导致节点状态太过光滑,并且属于节点自身的特征信息匮乏。
GGNN的改变
- 门控神经网络不再以不动点理论为基础了! 这意味着f不再需要压缩映射,迭代不需要收敛才能输出,隐藏层固定。可随之而来的问题是正确的初始化是ggnn最终的结果能否收敛且收敛至正确结果的关键。
- 加入了 GRU,即门控单元,把邻居节点的信息视为输入,节点本身的状态视作隐藏状态。 GRU的加入意味着不仅选择性记忆了邻居节点的隐藏信息,还选择性记忆了节点迭代过程中的隐藏信息。
- 针对不同类型的边引入了可学习的参数w。这样他就可以处理节点不同形式或边不同形式的图。
门控图神经网络
传播过程

观察上面门控图神经网络传播过程的式子,除了GRU的设计以外,还针对不同类型的边引入了可学习参数w,每一种边对应了一个权重,那么就可以处理可能存在边类型不同的图(异构图)了。
大致算法步骤
门控图神经网络PyTorch模型代码
论文地址:https://arxiv.org/abs/1511.05493
源码地址:https://github.com/calebmah/ggnn.pytorch
model.py
模型的框架如下所示:
GatedPropagation类
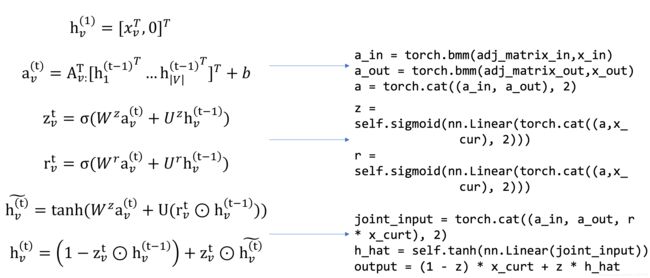
左边为上方“传播过程”的公式展开,右边是对应的伪代码(与源码不同)
- 令隐藏信息为一个二维向量,将第一个节点信息再加上一维的注释作为初始隐藏信息,这是第一个公式,是一个初始化过程,代码在模型外完成,因为第二维的注释是根据任务而定的。
- 第二个公式才是类的开始,将所有节点的上一时刻的隐藏信息与邻接矩阵相乘后以第三个维度拼接在一起。(注意这里的x与公式中的h对应)。ggnn在实现过程中将入度与出度分开考虑了,所以会有一个x_in一个x_out。
- z和r的求法相同,都是学习一个w,u的参数然后加和。因为求参数的过程也是相同的,所以可以先把a与x_cur(上一时刻的隐藏状态)先拼接,再求参数。加和过程实际上是源码中将nn.Linear设计为输出维度为输入维度的三分之一,这样就可以实现自动加和的结果。
self.gate_r = nn.Linear(self.hidden_dim*3, self.hidden_dim)
self.gate_z = nn.Linear(self.hidden_dim*3, self.hidden_dim)
- 最后一步与公式也是对应的。
GraphFeature类
我们首先要观察一下bAbI-tasks的任务

其中任务18与任务19都是基于整个图的输出,与其他基于某个节点的输出不同,所以我们必须寻找一个可将整张图的信息转化为一个隐藏信息向量的方法。
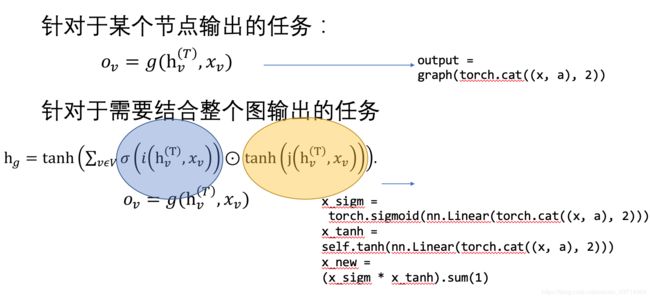
这涉及到注意力机制,蓝色部分用于计算节点v对于整个图的权重,黄色部分计算的是节点v的特征向量,因此,这个求和公式计算的就是所有节点构成的图的节点特征向量加权之和,即为图的特征向量(最后还要通过tanh激活函数)。整个公式看上去比较复杂,但核心思路应该就是这样。
输出部分位于GGNN类中。
def forward(self, x, a, m):
'''
init state x: [batch_size, num_node, hidden_size] , pad zero from annoatation
annoatation x: [batch_size, num_node, 1]
adj matrix m: [batch_size, num_node, num_node * n_edge_types * 2]
output out: [batch_size, n_label_types], for task 4, 15, 16, n_label_types == num_nodes
'''
x, a, m = x.double(), a.double(), m.double()
all_x = [] # used for task 19, to track
for i in range(self.n_steps):
in_states = self.fc_in(x)#将x喂入一层全连接求初始化隐藏信息并将注释用0填充。 形状:(batch_size, num_node,hidden_dim * n_edge)
out_states = self.fc_out(x)
in_states = in_states.view(-1,self.n_node,self.hidden_dim,self.n_edge).transpose(2,3).transpose(1,2).contiguous()#由于邻接矩阵的形状是(-1,self.hidden_dim,self.n_node*self.n_edge)为了满足矩阵乘法条件,必须将输入变形。第一个view将in_states变为(-1,self.n_node,self.hidden_dim,self.n_edge)然后第3,4维转置,2,3维转置。
in_states = in_states.view(-1, self.n_node*self.n_edge, self.hidden_dim)
out_states = out_states.view(-1,self.n_node,self.hidden_dim,self.n_edge).transpose(2,3).transpose(1,2).contiguous()
out_states = out_states.view(-1, self.n_node*self.n_edge, self.hidden_dim)
x = self.gated_update(in_states, out_states, x, m)
all_x.append(x)
if self.task_id == 18:#将图转化为特征向量后g函数输出
output = self.graph_aggregate(torch.cat((x, a), 2))
output = self.fc_output(output)
elif self.task_id == 19:
step1 = self.graph_aggregate(torch.cat((all_x[0], a), 2))
step1 = self.fc_output(step1).view(-1,1,self.n_output)
step2 = self.graph_aggregate(torch.cat((all_x[1], a), 2))
step2 = self.fc_output(step2).view(-1,1,self.n_output)
output = torch.cat((step1,step2), 1)
else:#直接进行g函数输出
output = self.fc1(torch.cat((x, a), 2))
output = self.tanh(output)
output = self.fc2(output).sum(2)
return output
创建邻接矩阵——将三元组变为邻接矩阵
'''
create_adjacency_matrix函数创建图的邻接矩阵,输入是样本中边列表、节点数、边类型数,返回值是样本的邻接矩阵。
值得注意的是,因为是有向图以及边有不同的类型,因此分别要为入射边和出射边结合不同的边类型建立邻接矩阵。
仍以任务18为例,创建过程是遍历边列表,对于每条边所对应的三元组(src,edge_type,tgt),
第一个数字表示源节点src,第二个数字表示边类型edge_type,最后一个数字表示目标节点tgt。
如果遍历到了三元组(src,edge_type,tgt),则将邻接矩阵中第(tgt-1)行到第(edge_type-1)*+(src-1)列的值置为1,
并将第(src-1)行第(edge_type-1+ |edge_type|)*+tgt-1列的值置为1,减1的原因是邻接矩阵的下标从零开始。
'''
def create_adjacency_matrix(edges, n_nodes, n_edge_types):
'''
Incoming and outgoing are separate
edge type is considered
'''
a = np.zeros([n_nodes, n_nodes * n_edge_types * 2])
for edge in edges:
src_idx = edge[0]
e_type = edge[1]
tgt_idx = edge[2]
a[tgt_idx-1][(e_type - 1) * n_nodes + src_idx - 1] = 1
a[src_idx-1][(e_type - 1 + n_edge_types) * n_nodes + tgt_idx - 1] = 1
return a
创建完邻接矩阵,整个模型就差输入部分了,我们具体任务具体分析。
以task-18为例
将任务转换成适宜 GGNN 模型的形式,转换过程为将任务中的一个完整描述转换为一系列实体之间的关系,然后再转换成单个图。每个实体映射为一个节点,实体之间的关系映射为带有标签的边。task-18是个关于大小的推理问题,每个样本中都有几条线索,利用这些线索作为已知条件,这些线索可以用图来表示。对整个图进行学习后将模型用于问题解答,最终输出1或0,转化成一个二分类问题。

问题中的fits in和smaller than 都可以转化成小于的意思,于是我们令“<”=1。可用“?”作为问题的开始标志,yes,no可用1,2表示,最终将整个数据转化为了上图所示的形式。
我们令第一列为头节点,第二列为尾节点,就可以将这一堆数据变成一幅图:

如5到1有一条边,4到2有一条边,总共是9条边。
data.py
程序所用数据保存在 babi_data 文件夹中,其包含 10 个处理后的文件夹,每个文件夹包含训练数据文件夹,测试数据文件夹,因为Li 等人[7]用 RNN 作为基准与 GGNN 模 型的性能进行比较,所以文件中还包含了用于 RNN 模型训练、测试的数据,而该实现 分析针对的是 GGNN 模型,所以关于 RNN 模型的数据不进行讨论。每个训练、测试文件夹中包含 4、15、16、18、19 共 5 个 babi 任务,每个任务由 edge_types,graphs,labels, node_ids,question_types 共 5 个文件组成。文件构成如图所示:

我们在介绍各个函数的部分来介绍这些文件的具体功能。
data.py程序结构如下:
-
get_data_types函数
- edge_types 记录边 id 与边类型的对应关系,边类型可以由自然语言或符号表示。
- labels 记录答案数字与实际含义的对应关系。
- node_ids 文件记录节点 id 与节点名称的对应关系。
- question_types 记录问题 id 与问题类型的对应关系。
因为 edge_types,labels,node_ids,question_types 四个文件中的数据格式皆为‘?’=‘?’ 这样的等式,所以可以使用同一个函数处理。处理时,首先以‘=’号对读入的每行按照 行分割,得到长度为二的字符串 line_tokens,然后以格式{key:linetoken[0],map: linetoken[1]}建立字典,处理完毕后返回字典。示例结果如上图所示。代码如下所示。
#get_data_types函数得到数据文件中定义的字典。
#函数输入为文件路径,返回是字典(键值对)形式的数据。
#因为edge_types,labels,node_ids,question_types四个文件中的数据格式皆为‘?’=‘?’这样的用等式表示的字典形式
#所以可以使用同一个函数处理。
#处理时,首先以‘=’号对读入的每行按照行分割,得到长度为二的字符串line_tokens,
# 然后以格式{key:linetoken[0],map:linetoken[1]}建立字典,处理完毕后返回字典。
def get_data_types(data_path):
'''get edge/label/node/question type dictionary'''
data_type = {} #存储字典形式的数据,以便作为函数的返回值返回
with open(data_path,'r') as f:
for line in f:
if len(line.strip()) == 0:
pass
else:
line_tokens = line.strip('\n').split("=")
assert(len(line_tokens)==2)
data_type[line_tokens[0]] = line_tokens[1]
return data_type
-
load_graph_from_file函数

每个样本由边序列以及问题序列组成,每个问题行都是由‘?’起,且各样本之间空一行。处理的时候判断当前行是否为空,如果非空,继续判断起始字母是否为‘?’, 是的话则将当前行按问题处理,将‘?’省略,其余数字添加到定义的 target_list 列表 中,该列表保存单个样本的所有问题。如果不是由‘?’起,代表当前正在处理行是图 中的一条边,直接将该行所有数字添加到定义的 edge_list 列表中,该列表存储当前正在 处理样本的所有边。如果当前行为空,代表一个样本处理完毕,则将 edge_list,target_list 一起作为一个元素添加到定义的 data_list 列表中。代码如下所示:
#load_graphs_from_file函数用于从存储图结构和问题信息的原始文件读入数据。
# 根据x_graph.txt文件所示的原始文件格式,每个样本由边序列以及问题序列组成,每个问题行都是由‘?’起,且各样本之间空一行。
# 处理的时候判断当前行是否为空,如果非空,继续判断起始字母是否为‘?’,是的话则将当前行按问题处理,将‘?’省略,
# 其余数字添加到定义的target_list列表中,该列表保存单个样本的所有问题。
# 如果起始字母不是‘?’,代表当前正在处理行是图中的一条边,直接将该行所有数字添加到定义的edge_list列表中,
# 该列表存储当前正在处理样本的所有边。
# 如果当前行为空,代表一个样本处理完毕,则将edge_list,target_list一起作为一个元素添加到定义的data_list列表中。
# 对于每个数据集,data_list列表的长度为1000,代表1000个训练样本。
def load_graphs_from_file(file_name):
'''
load graph data from file
output = [data_size, 2, (num_fact/num_question), 3/num_answer]
'''
data_list = []
edge_list = []
target_list = []
with open(file_name,'r') as f:
for line in f:
if len(line.strip()) == 0:
data_list.append([edge_list,target_list])
edge_list = []
target_list = []
else:
digits = []
line_tokens = line.split(" ")
if line_tokens[0] == "?":
for i in range(1, len(line_tokens)):
digits.append(int(line_tokens[i]))
target_list.append(digits)
else:
for i in range(len(line_tokens)):
digits.append(int(line_tokens[i]))
edge_list.append(digits)
return data_list
-
data_convert函数
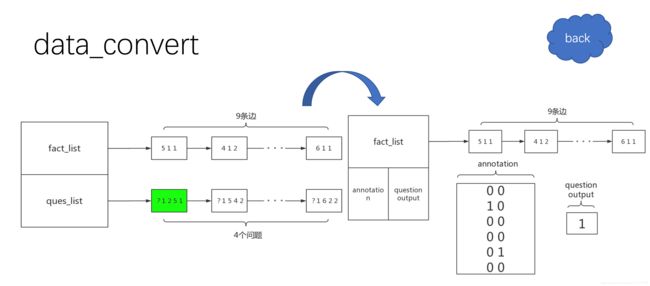
通过前面的处理,数据变为左边所示的形式,但是这样的结构不能用于训练任务 18 类似于上面提到的可达性问题,所以,设置起始点的注释为[1,0],中止点注释为[0,1],其余节点都是[0,0]。例如,图 3-9 中绿色标记的问题处理 后的结果如右边所示,将每个问题转化为annotation将问题的结果转化为question output。代码如下
#data_convert函数对通过load_graphs_from_file从图和问题原始文件中读入数据进行预处理,
#因为未经处理的数据中,一个样本中只包含一个图,而包含多个问题,这样并不能用于训练,
# 所以在此将样本中的图根据其对应的问题个数扩充,使图与问题一一对应。
# 例如在胡兴航论文中图3-2所示的数据中,样本包含图3-3所示的一个图,而该图对应于图3-2中10-13行所示的四个问题,
# 所以需要将图复制四次,与每个问题一一对应。
# 原文中,GGNN相较于GNN以及LSTM一大特点是可以在一些bAbi任务上,只需要小得多的样本进行训练即可获得完美的测试精度,
# 故转换的时候并不将1000个训练样本全部转换,而是只转换train_size个样本,train_size的默认值为50,
# 因为原文中GGNN模型只需50个训练样本进行训练,就可在4、15、16、18任务上达到百分百测试准确率。
# data_convert函数的输入包括需要转换的数据data_list(由load_graphs_from_file函数返回)、节点注释维度、节点个数、问题个数、以及任务id。
# 首先,根据问题个数定义task_data_list列表的长度,以任务18举例,该任务只有一种问题类型,所以列表长度为1。
# 接着遍历数据列表,对于每个列表项,遍历包括的所有问题,对于每个问题,所对应的正确答案(即问题的真假值)对应于最后一个数字,
# 然后创建节点注释,任务18类似于Li等人[7]在论文中讨论的中可达性问题,
# 所以,设置起始点的注释为[1,0],中止点注释为[0,1],其余节点都是[0,0]。
# 然后将样本中的图,节点注释,以及正确结果一起作为一个元素,添加到task_data_list中。
# 因为每个样本中的图对应的问题个数可能不止一个,而data_convert函数预处理后每个样本中图与问题一一对应,
# 所以task_data_list的长度不是train_size,而会变大。
def data_convert(data_list, n_annotation_dim, n_nodes, n_questions, task_id):
'''
data_preprocessing
separate by answer type
data_list: [data_size, 2, (num_fact/num_question), 3/num_answer] 什么意思?
n_annotation_dim: original feature of node(不同任务的特征向量维度不一样,这在config.py中的ANNOTATION_DIM定义)
n_nodes: Number of nodes
n_questions: Number of question types
'''
task_data_list = []
for i in range(n_questions):
task_data_list.append([])
for item in data_list:
fact_list = item[0] #对应图数据
ques_list = item[1] #对应问题列表
for question in ques_list: #对于每个问题,都会在对应的问题类型队列中加入图数据,所以有多少个问题,就会有多少个任务数据放入task_data_list
question_type = question[0]
if task_id == 19: #task_id为19对应任务18么?
question_output = np.zeros([2 if task_id == 19 else 1])
assert(len(question) == 5)
question_output[0] = question[-2]
question_output[1] = question[-1]
else:
question_output = np.array(question[-1])
annotation = np.zeros([n_nodes, n_annotation_dim]) #所有节点的特征向量均初始化为0
for i_anno in range(n_annotation_dim):
annotation[question[i_anno + 1]-1][i_anno] = 1 #question[i_anno + 1]对应初始和终止节点id(i_anno分别取0和1时)
task_data_list[question_type-1].append([fact_list, annotation, question_output])
return task_data_list
get_loader and BABI class

BABI 类对数据进行封装,定义了节点类型数,边类型数等关于数据的描述,以及 __len__函数和__getitem__函数让该类可用于进行数据的检索,每次检索的返回内容是邻接矩阵,节点注释,正确结果。
get_loader 函数返回 BABI 类型的对象以及一个数据 加载器。数据加载器包含 BABI 类型的对象,且设置了批处理的大小以及是否打乱等常用参数。
main.py

main的主要作用是接受命令行的参数,定义参数之后,通过解析 parser 得到 opt,然后 main.py 将 opt 作为参数调用 train.py 中的 train 函数训练模型,之后对训练后的模型进行测试。
train.py

接着从 babiloader 中得到邻接矩阵、节点注释以及目标输出,并对节点注释进行零填充得到初始节点表示,然后将邻接矩阵、节点表示和目标输出作为参数用对象 net 预测输出。