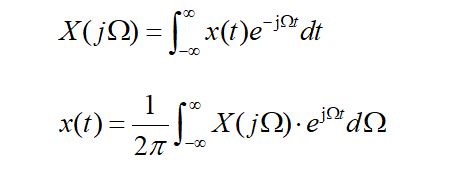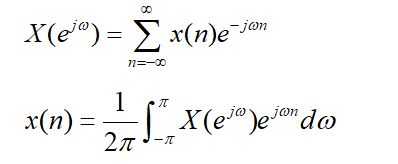信息与通信工程学科面试准备——DSP
面试准备——DSP
经过信号与系统学习,我们知道连续的周期信号可以通过傅里叶级数的方式得到其频谱为离散的线状谱,对于周期无限大的连续信号,可以通过傅里叶变换得到连续的频谱。那么DSP这门课将带我们走进离散(周期or非周期)序列的频谱是什么样子呢?
已知连续序列的变换函数:
1. z变换与傅里叶变换的关系:傅立叶变换是单位圆上的Z变换,单位圆必须包含在收敛域中。当z变换收敛域包含单位圆时,可以根据z变换后的函数,将z=e^jw代入即可。
2.逆z变换的方法:部分分式展开、围线积分法、幂级数法
3.系统函数H(z)的零极点分布:
①零极点分布将影响系统的频率特性
极点影响幅频特性的峰值,峰值频率在极点的附近;
极点越靠近单位圆,峰值越高,越尖锐;
极点在单位圆上,峰值幅度为无穷,系统不稳定。
零点影响幅频特性的谷值,谷值频率在零点的附近;
零点越靠近单位圆,谷值越接近零;
零点在单位圆上,谷值为零。
处于坐标原点的零极点不影响幅频特性
该方法适于低阶系统
②极点分布影响系统的因果性和稳定性
因果性:因果序列Z变换的所有极点在以Rx-为半径的圆内。
稳定性:方法一:序列h(n)绝对可和,方法二:系统函数的收敛域包含单位圆
因果稳定系统:系统函数的极点在单位圆内,且收敛域包含单位圆
4.DFT提出的目的
序列的傅里叶变换、Z变换是时域离散信号及系统分析与设计的重要数学工具;但变换结果均为连续函数,无法用计算机进行处理;离散傅里叶变换(DFT)对有限长时域离散信号的频谱进行等间隔采样,频域函数被离散化了,便于信号的计算机处理。
5.DFT与DFS、ZT、FT的关系
①有限长序列x(n)的DFT变换X(k),就是x(n)的周期延拓序列的DFS系的主值序列
②序列x(n)的N点DFT是 x(n)的Z变换在单位圆上的N点等间隔采样;X(k)为x(n)的傅立叶变换在区间[0,2pi]上的N点等间隔采样
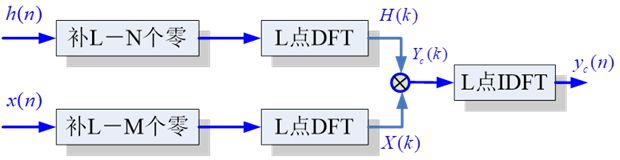
6.满足L>M+N-1,循环卷积等价于线性卷积;且时域循环卷积转换到频域即为频域乘积
序列h(n)与x(n)的长度分别为N和M,则其循环卷积结果yc(n)计算方法如下:
7.离散巴塞伐尔定理表明:序列在时域计算的能量等于其在频域计算的能量
8.由X(k)恢复出x(n)的条件(即频域采样定理)
①x(n)序列长度有限
②采样点数N大于x(n)序列长度M
9.由X(k)恢复出X(z)或者X(e^jw)(即内插公式)
10.基2FFT算法:将时域序列逐次分解为一组子序列,利用旋转因子的特性,由子序列的DFT来实现整个序列的DFT
11.带通信号采样:最低频率fl,最高频率fh,带宽fb=fh-fl则若最高频率fh=K*fb即为带宽的整数倍时,采样频率为2fb即可。若fh不为带宽整数倍,则需要降低fl即扩展带宽即可。
12.用DFT(FFT)对模拟信号进行谱分析的误差来源:频谱混叠(增加预滤波器)、栅栏效应(增加采样点数)、截断效应(改变窗函数形状,增大主瓣能量)
13.数字滤波器的可实现性
①因果稳定,系统传输函数的极点都在单位圆内
②实数乘法,系统函数的系数为实数,即零极点须共轭成对出现,或者是实数
14.理想滤波器是个物理不可实现的非因果系统
原因:从h(n)看,n<0时已有值。
15.简单滤波器的设计
基于零极点配置的的简单滤波器设计方法
原理:
①极点靠近单位圆,频率响应的峰值越高;极点放在需加强的频率点附近
②零点靠近单位圆,频率响应的谷值越小;零点放在需减弱的频率点附近
约束条件:
①极点在单位圆内,保证滤波器的因果稳定;
②零、极点须共轭成对,或者是实数,保证系统函数系数为实数。
16最小相位滤波器
因果、稳定的离散系统H(z)要求极点必须全部位于单位圆内,而对零点的位置没有要求,可以在圆内,也可以在圆上或是圆外。这样
如果该系统的零点全部在单位圆内,称该系统为最小相位系统。
如果该系统的零点全部在单位圆外,称该系统为最大相位系统。
如果圆内和圆外都有零点,称该系统为混合相位系统
17.任何一个非最小相位系统的系统函数H(z)均可以由一个最小相位系统和一个全通系统级联而成
意义:将系统位于单位圆外的零(极)点用共轭倒易的点代替时,不会影响系统的幅频响应特性。这一点在滤波器设计中,将单位圆外的极点用其镜像代替,确保DF因果稳定
作用:利用级联全通函数的方法,可将非最小相位系统的零点反射到单位圆内,而构成幅度响应相同的最小相位延时系统。
18.典型滤波器
巴特沃斯(Butterworth)滤波器:具有单调下降的幅频特性;
切比雪夫(Chebyshev)滤波器:幅频特性在通带或阻带有波动,可提高选择性;大约3/4通带接近线形相位;
贝塞尔(Bessel)滤波器:通带内较好的线性相位;
椭圆(Ellipse)滤波器:通带和阻带内波纹固定时,阶数越高,过渡带越窄。较好的线性相位。大约1/2通带接近线形相位;
19.典型滤波器对比
1.相同指标下,椭圆滤波器阶次最低,切比雪夫次之,巴特沃思最高,参数的灵敏度则恰恰相反。
2.相同通带最大衰减、阻带最小衰减,巴特沃思滤波器的过渡带最宽;椭圆滤波器过渡带最窄;
3.切比雪夫1滤波器通带等波纹幅频特性,过渡带和阻带单调下降,大约3/4通带接近线性相位;
切比雪夫2滤波器阻带等波纹幅频特性,通带和过渡带单调下降,大约3/4通带接近线性相位;
4.椭圆滤波器通带、阻带等波纹幅频特性,过渡带单调下降,仅在1/2通带接近线性相位
20.设计滤波器时考虑的指标:通带边界频率、阻带边界频率、通带最大衰减、阻带最小衰减
21.IIR数字滤波器设计
间接法设计过程:
1.确定数字滤波器的指标
2.转换成过渡模拟滤波器的指标
3.设计过渡模拟滤波器
4.将过渡模拟滤波器转换为数字滤波器
其中第四步将过渡模拟滤波器转换为数字滤波器的要求有:保证因果稳定性(即将左半平面映射到单位圆内)、H(z)的频响要能模仿Ha(s)的频响(即将虚轴映射到单位圆上)
两种常用的映射变换方法:脉冲响应不变法、双线性变换法
21.1.脉冲响应不变法
基本思想:使数字滤波器能模仿模拟滤波的特性;
从滤波器的脉冲响应出发,使数字滤波器的单位脉冲响应序列h(n)正好等于模拟滤波器的冲激响应ha(t)的采样值。

数字滤波器的频响并不是简单的重现模拟滤波器的频响,而是模拟滤波器频响的周期延拓

脉冲响应不变法的最大缺点:有频谱周期延拓效应,因此只能用于带限的频响特性,如衰减特性很好的低通或带通,而高频衰减越大,频响的混淆效应越小,至于高通和带阻滤波器,由于它们在高频部分不衰减,因此将完全混淆在低频响应中,此时可增加一保护滤波器,滤掉高于ws/2的频带,再用脉冲响应不变法转换为数字滤波器,这会增加设计的复杂性和滤波器阶数,只有在一定要满足频率线性关系或保持网络瞬态响应时才采用。
21.2.双线性变换法(克服脉冲响应不变法的频谱混叠现象)
基本设计思想:
脉冲响应不变法:波形逼近
双线性变换法:算法逼近。用线性常系数差分方程逼近线性常系数微分方程
缺点:非线性关系消除了频率混叠,但会带来幅度和相位失真。
22.【总结】四种线性相位FIR DF特性
第一种情况 ,h(n)偶、N奇,四种滤波器都可设计
第二种情况, h(n)偶、N偶,可设计低、带通滤波器,不能
设计 高通和带阻。
第三种情况, h(n)奇、N奇,只能设计带通滤波器,其它滤
波器都不能设计。
第四种情况, h(n)奇、N偶,可设计高通、带通滤波器,不
能设计低通和带阻。
四种FIR数字滤波器的相位特性只取决于h(n)的对称性,而与h(n)的值无关。幅度特性取决于h(n)。设计FIR数字滤波器时,在保证h(n)对称的条件下,只要完成幅度特性的逼近即可。
23.FIR滤波器的设计方法
1.基于逼近理想滤波器特性的方法有以下三种:
窗函数法(时域逼近)
频率采样法(频域逼近)
等波纹最佳逼近法(等波纹逼近)
2.最优设计法
设计思想:保证线性相位,逼近理想滤波器
23.1窗函数法(时域逼近)设计FIRDF
设计过程:
1.构造希望逼近的理想滤波器,如:理想低通滤波器
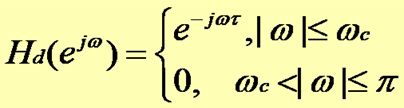
2.求hd(n),其为无限长、非因果
3.用窗函数法设计FIR滤波器,时域加窗
其中第三步用窗函数法设计FIR滤波器:
选择窗函数的类型和长度方法:
①根据阻带最小衰减 选择窗函数的类型
原则是:在保证阻带衰减满足要求的情况下,尽量选择主瓣窄的窗函数。
②根据过渡带的宽度选择窗函数的长度
23.1.1对hd(n)加矩形窗处理后,其频率响应的几点影响:
①改变了理想频响的边沿特性,形成过渡带
②通带、阻带均有纹波,纹波取决于旁瓣,旁瓣幅度大,纹波幅度大,与窗口长度 N无关。(决定于窗口形状)
且需要明确:
①N增加,过渡带宽减小,肩峰值不变。
②N的变化不能改变主瓣与旁瓣的比例关系,只能改变绝对值大小和起伏的密度,当N增加时,幅值变大,起伏变密,而最大肩峰永远为8.95%,这种现象称为吉布斯(Gibbs)效应。
总结:选择窗函数的要求:
① 窗谱主瓣宽度要窄,以获得较陡的过渡带;
② 相对于主瓣幅度,旁瓣要尽可能小,使能量尽量集中在主瓣中,这样就 可以减小肩峰和余振,以提高阻带衰减和通带平稳性。
然而,实际上这两点不能兼得,一般总是通过增加主瓣宽度,即加宽过渡带为代价,来换取对旁瓣的抑制。
23.1.典型的窗函数
矩形窗
三角窗
升余弦(汉宁)窗
改进升余弦(哈明)窗
布莱克曼窗
凯塞窗:以上五种窗函数,滤波器的阻带衰减是固定的。不同的窗函数通过增加主瓣宽度为代价来降低旁瓣。凯塞窗则可自由选择主瓣宽度和旁瓣衰减;对于给定指标,其滤波器阶数最小
24.频率采样法设计FIRDF
设计步骤:
1.根据阻带最小衰减,选择过渡带采样点的个数m
2.确定过渡带宽度,估算滤波器长度N
3.构造希望逼近的频率响应函数
4.频域采样 H(k)
5.求h(n)
6.检验设计结果,微调边界频率
频率采样设计法的优点:
① 直接从频域进行设计,物理概念清楚,直观方便;可以设计任意形状频率响应特性的FIRDF;
② 适合于窄带滤波器设计,这时频率响应只有少数几个非零值。
典型应用:用一串窄带滤波器组成多卜勒雷达接收机,覆盖不同的频段,多卜勒频偏可反映被测目标的运动速度;
缺点:截止频率难以控制。
因频率取样点都局限在2π/N的整数倍点上,所以在指定通带和阻带截止频率时,这种方法受到限制,比较死板。 充分加大N,可以接近任何给定的频率,但计算量和复杂性增加。
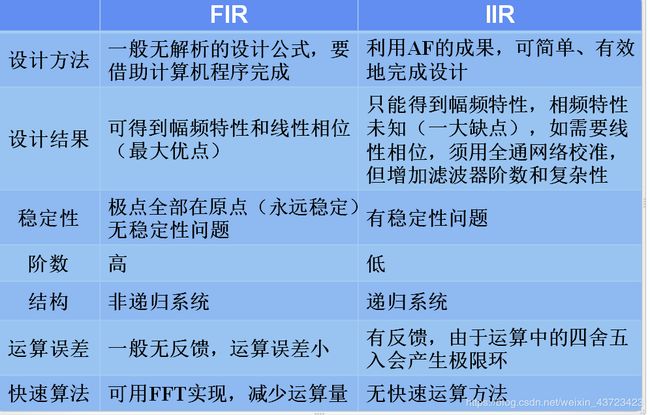
25.IIR与FIR数字滤器的比较
26.时域离散系统的实现
均由延迟、乘法、加法实现
- FIR数字滤波器的网络结构
直接型结构
级联型结构
线性相位型结构
频率取样型结构
快速卷积法 - IIR数字滤波器的基本结构
直接型结构
级联型结构
并联型结构