竞赛常用STL容器详解
竞赛常用STL容器详解
- 一、 概述
- 二、 迭代器
- 2.1.迭代器与遍历
- 2.2. 迭代器失效
- 2.3. 尾后迭代器
- 三、 Vector
- 3.1.总览
- 3.2.常见用法
- 四、List
- 五、Stack
- 5.1.总览
- 5.2.常见用法
- 六、Deque及其延伸
- 6.1.Deque
- 6.2.Queue
- 6.2.1.总览
- 6.2.2.常见用法
- 6.3.Priority_Queue
- 6.3.1.总览
- 6.3.2.常见用法
- 七、Set及Multiset
- 7.1. 总览
- 7.2. 常见用法
- 八、Map
- 8.1. 总览
- 8.2. 常见用法
- 九、总结
一、 概述
在算法竞赛中,使用C++语言的占很大比例,而几乎没有人使用C语言,其中核心的原因就是C++包含STL容器库,能够极大地减少选手在赛场上为了一些基础数据结构而浪费的时间。诚然,花一两分钟实现一个stack、queue甚至priority_queue都不是什么大问题,但如果需要实现BBST(Balanced Binary Search Tree)的情况呢?如果可以的话,我们总是希望不要手写红黑树、动态数组的。那么STL容器库的出现就像雪中送炭一样了。它们覆盖了竞赛中最基础的需要(张昆玮树、主席树这种东西肯定不会包含的),让你在面对非数据结构题的时候能够不因数据结构部分的代码而分心。
关于STL容器的相关问题非常细,经常成为面试中的考题,这里我们仅讨论一些必须的内容,然后只谈论在竞赛中的具体使用。
首先给出一张表格(来自cppreference):
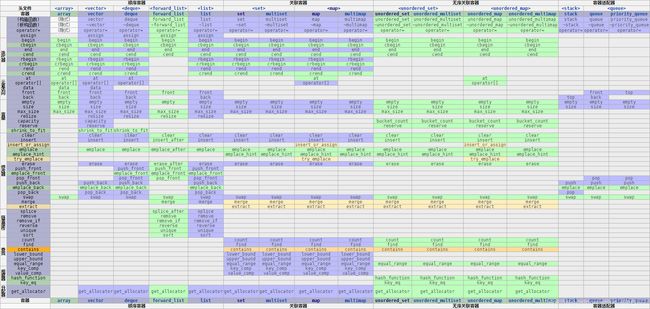
这张表格中给出了各种容器支持的成员函数,在大多数停留在C++14和C++11版本的测试平台中,只有紫色、绿色部分是可用的。
在考察具体的容器的时候,出于竞赛中的需要,我们不会涵盖以上的全部,而是着重关注以下几点:
- 随机访问
- 插入和删除
- 端点访问
- 迭代器类型(总结以上几点)
- 时间复杂度
事实上,综合以上几点,就可以得出一个容器的作用。容器的作用是由它支持的操作及其时间复杂度决定的,并不是说,容器的名字叫做set我就一定把它当作集合来用。从ADT的角度来说,数据结构=接口+接口的复杂度。而从另一个角度来看,容器内部支持的逻辑操作决定了它能够使用的迭代器类型,而这决定了外部可能存在哪些接口,因此也可以说数据结构=内部存储+迭代器。这样两种观点,能够在使用的层面加强我们对于STL容器的理解。
方便起见,这里先列出一个汇总的表格,包含了竞赛中常用的几种数据结构:
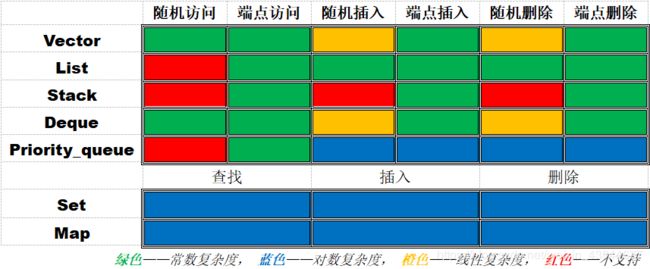
这里的表格只给出了很简单的内容,本文末尾会给出两个总结性的表格,给出具体操作的函数名和时间复杂度。
二、 迭代器
2.1.迭代器与遍历
操作一个容器,无法脱离它提供的工具——迭代器。即使没有使用过容器,我们也一定使用过最基本的方式遍历一个数组:
for (int i = 0; i <n;i++)
//......
不严格地说,这里的”i”就可以视作一个最原始的迭代器。事实上,对于藉由它,我们可以访问一个容器内的全部内容——这就是我们所说的“遍历”,这能够让我们对内部数据进行基于元素的操作。
事实上,一个真正的迭代器需要符合很多要求。STL容器所配备的迭代器都属于C++迭代器库规定的六种之一,它们是:
- 遗留输入迭代器
- 遗留向前迭代器
- 遗留双向迭代器
- 遗留随机访问迭代器
- 遗留输出迭代器
- 遗留连续迭代器
这些名字看起来很唬人,让我们来一点一点解释。
首先,它们都是“遗留迭代器”,这意味着它们都:(以下假设i是迭代器)
- 可解引用(*i得到元素)
- 可前自增(++i得到下一位置)
这也就是为何我们能藉由迭代器来完成遍历容器内元素的操作。
下面给出上文提到的六种迭代器的实际含义,虽然大多数情况下竞赛中用不到这些原理,但偶尔会有基于手动遍历的技巧性操作,这时候也许需要你对迭代器有一定的认知:
遗留输入迭代器:
在遗留迭代器的基础上,
- 可不等比较(i!=j有定义)
- 可后自增(i++有定义)
但:**自增后,先前值可能失效。**也就是说,当你访问第1个元素时,可能无法通过这个迭代器的拷贝访问第0个元素。
遗留向前迭代器:
在遗留输入迭代器的基础上,
- 自增后保证先前值不失效。
遗留双向迭代器:
在遗留向前迭代器的基础上,
- 可前自减(–i有定义)
- 可后自减(i–有定义)
遗留随机访问迭代器:
在遗留双向迭代器的基础上,
- 有下标运算符(i[n]有定义)
- 有比较运算符(>、<、>=、<=有定义)
- 可按增量移动(+、-、+=、-=有定义)
且:迭代器移动只耗费常数时间。
若以上迭代器满足遗留输出迭代器的标准,那么称它们是“可变迭代器”。
遗留输出迭代器:
在遗留迭代器的基础上:
- 可赋值(*i=something有定义)
- 可后自增
若以上迭代器满足遗留连续迭代器的标准,那么称它们是“连续迭代器”。
遗留连续迭代器:
在遗留迭代器的基础上:
- 逻辑相邻元素在内存中也相邻,
- 即:
*(i + n)等价于*(std::addressof(*i) + n)
以上涉及的运算,不仅需要定义,并且需要符合功能要求。同时,部分操作有特例存在。例如,即使迭代器可解引用,也无法对尾后迭代器或孤立迭代器解引用。
那么,如果知道某个容器的迭代器类型,对比一下它们支持的操作,你就能知道自己的一些奇思妙想能否实现了。例如:两头向中间访问、一次跳过多个元素、多个迭代器同时访问……
那么,在复杂的环境下,例如访问的同时涉及插入和删除,这些操作还能按照我的意图运行吗?这就是我们要讨论的下一个问题了。如果说以上内容更偏向于实务开发,那么这个问题在竞赛中就更加常见了,它就是“迭代器失效”问题。
2.2. 迭代器失效
容器的一些操作会使得先前声明的迭代器失去它应有的作用,这种限制来自于容器底层的实现。例如在vector中,即使在尾部插入一个新元素也可能因为导致空间达到临界值而使得数据全部被移动到新空间,从而使全部迭代器失效。
大体来说,删除总会使得迭代器失效,而插入有些情况会使其失效。具体的情形见下表:(同样来自cppreference)
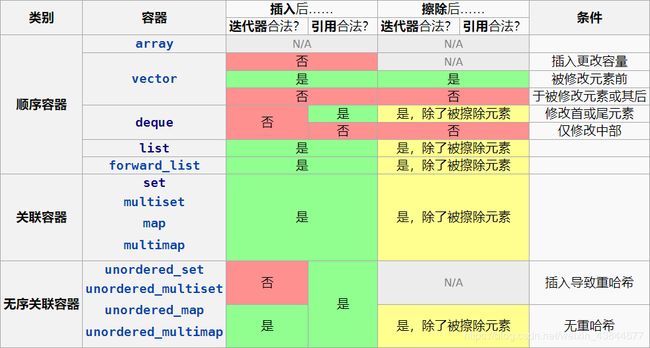
除此之外,尾后迭代器有一些特殊情形需要考虑,例如vector的尾后迭代器总是会被非法化、除了删除首元素外的修改操作都会非法化deque的尾后迭代器,等等。
2.3. 尾后迭代器
另一个要注意的点是,一般来说一个容器的begin()返回的是指向容器内首个元素的迭代器,而end()指向的却不是尾部元素,而是尾后——一个不存在的元素,我们也常常把这种位置称为“哨兵”。这一点好像恰好和其他参数为一个区间的函数,如sort(), substr()等,对应了起来——似乎编程中所有涉及区间的操作,都是使用左开右闭区间来表示的——也就是说,end()表示尾后。这是为什么呢?
考虑对一个具有普通遗留迭代器的容器进行迭代,应当怎么写呢?似乎很简单:
for (auto i = x.begin(); i != x.end(); i++)
看到这里,你应当已经明白了:大多数容器不具有遗留连续迭代器的性质,那就不存在像i < x.end()这种操作,因此无法像迭代一个数组一样以一个偏序比较作为条件,那么就必须有一个哨兵作为实际可以访问到的截止位,这个哨兵就是end()。
三、 Vector
3.1.总览
那么,我们就开始讲每个具体的容器了。在各节中,我们会依次介绍每个容器的用途、迭代器类型、插查删操作及其复杂度,有必要的时候,我们还会介绍一些其他的小trick。

我们看到,Vector与其他STL容器最大的区别就在于,只要元素不为bool类型(bool类型因内存对齐而不连续),它是唯一使用连续迭代器的,即使对于全部情况,它也符合遗留随机访问迭代器,从而支持以常数复杂度通过下标运算符随机访问。这使得我们可以直接将其作为升级版的数组使用——数组的功能全部被它继承,而它又自带了其他一些便捷的函数——因此vector又被称为**“动态数组”**。
它底层的数据结构使用的是静态数组,实现动态扩容的奥秘在于,它在每一次容量占用达到阈值时就进行一次翻倍扩容,从而保证了均摊 O ( 1 ) O(1) O(1)的时间复杂度,而又能节省空间。
3.2.常见用法
在C++11中,在具有begin()和end()的范围上进行迭代,有一种简便写法,那就是
for (auto& v : container)
它等价于
for (auto& v = container.begin(); v != container.end(); v++)
这里的auto利用了C++11的另一个特性——类型推导,这只是一个语法糖,它使我们不必写上container::iterator这一串复杂的类型,而在程序运行中与完整键入的并无区别。而auto后面加的&代表v是一个左值引用,那么我们就可以通过v来修改容器中的元素。而如果我们想避免这种修改,可以去掉&,这时v就是一个右值拷贝。
以一个int类型动态数组为例,我们可以这样输出:
vector<int> arr;
for (auto v : arr)
cout<<v;
而读入可以这样写:
for (int i = 1; i <= n; i++)
{
cin>>temp;
arr.push_back(temp);
}
当然,同程序员们默认的一样,它的下标是从0开始的。
vector是否可以写高维数组呢?如果你经常在Leetcode上刷题,应当见过二维数组的这种写法:vector。高维数组以此类推即可。在访问上,这种写法与int arr[][]没有任何区别。
四、List
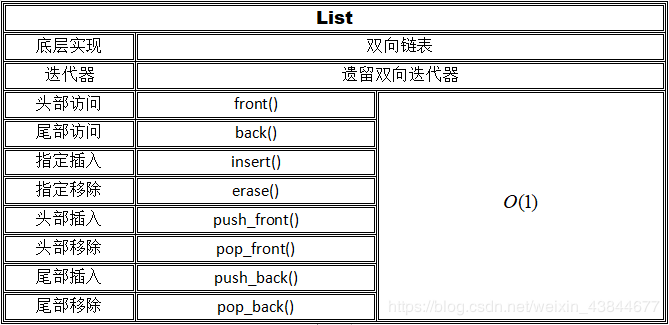
可以看到,list实际上就是一个双向链表,因此对于插入和删除的操作具有优秀的时间表现。当然也很容易想到,list是无法实现常数时间随机访问的,insert和erase看起来时间复杂度为 O ( 1 ) O(1) O(1),但在实际应用中,找到插入位置往往就需要 O ( n ) O(n) O(n)的时间。
与list相似的,STL中还存在一个单向链表forward_list。由于不需要反向链,它的空间占用有所减小,不过这一点在竞赛中不怎么需要,所以那种结构了解即可。
五、Stack
5.1.总览
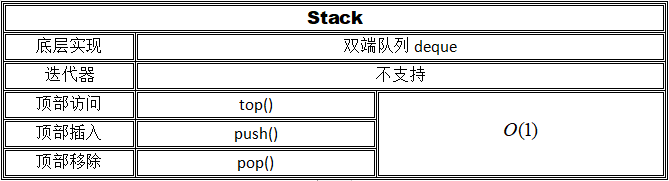
相比于精心构造的数据结构,stack似乎更应当被称为一种“包装器”,它在底层实现的基础上屏蔽掉了一些功能,从而使自身表现得更像一个物理栈。对于它和queue,我们不需要多费口舌,也许这是仅有的两种我们可以自己实现而不会使代码冗长的数据结构了。但无论怎么说,有一个构造好的容器使用总是好的,它可以防止我们在底层的操作上犯一些愚蠢的错误。
5.2.常见用法
那么,这里就实际给出使用stack完成DFS的过程,以下是一段代码片段:
vector<int> edges[N];
stack<int> dfs;
/*............*/
dfs.push(v0);
vis[v0] = true;
while (!dfs.empty())
{
bool tag = false;
int now = dfs.top();
prt.push_back(now);
for (auto v : edges[now])
if (!vis[v])
{
dfs.push(v);
vis[v] = true;
tag = true;
break;
}
if (!tag)
dfs.pop();
}
六、Deque及其延伸
6.1.Deque
虽然实际使用时很少见,但deque是很多STL容器的基础,stack和queue都由它封装而来,它也支持相当多的操作,详见下表:
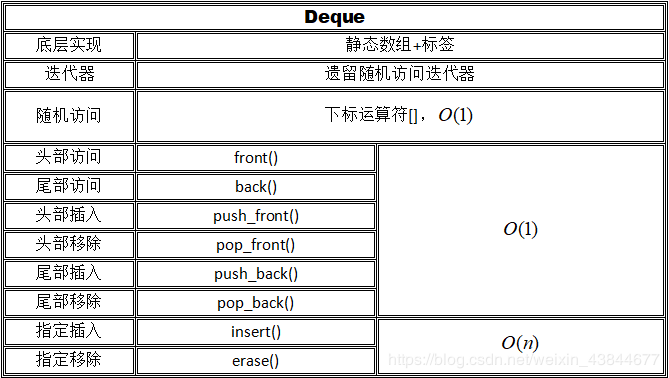
值得注意的是,该容器的迭代器非法化情形比较有趣,其原理也是面试题常考的内容,建议结合STL源码深入分析。
结合上表,发现它与List的区别主要在于,它能够实现常数时间随机访问,但内部插入、删除却需要线性时间,这也符合他们底层实现:链表和数组的区别,也正是这一点使得它们的迭代器一个是双向而另一个是随机访问。多进行这种思考,由底层实现——容器——迭代器——操作转为底层实现——迭代器——操作,是一名程序员获得抽象思维的重要方式。
6.2.Queue
6.2.1.总览

queue就是我们常说的队列了。同stack一样,它是很常见而且简单的数据结构,同样由deque封装得来。当然,由于deque和list都满足它的底层实现的要求,因此你可以指明换用list作为你的queue的底层实现:
queue<int, list<int>> myQue;
由于STL容器都使用模板类,因此在实际开发中,你完全可以将所有容器的分配器、底层容器自主实现。
6.2.2.常见用法
queue用来实现BFS应该是最常见的用法了,以下和stack一样给出一个代码片段:
queue<int> que;
while (!que.empty())
{
int now = que.front();
que.pop();
if (success(pos[now]))
return true;
for (int i = 0; i < n; i++)
if (!vis[i] && dis[now][i] <= limit)
{
que.push(i);
vis[i] = true;
}
}
6.3.Priority_Queue
6.3.1.总览

priority_queue实现了优先队列这一ADT,也就是我们常说的**“堆”**。但要明晰的是,优先队列是一种ADT,而堆是它的一种具体实现。在默认状态下,priority_queue实现的是大根堆,但你可以通过模板特化从而实现小根堆,甚至是自己定义的规则。
6.3.2.常见用法
实现小根堆的方式很简单:
priority_queue<int, vector<int>, std::greater<int>> myHeap;
其中第一个参数为元素类型,第二个类型为底层实现,默认为vector,但STL库中的deque也符合要求。第三个参数为你的比较类型。priority_queue会按照这一比较偏序将最末序的元素作为“最大元素”。
在sort函数中自己构造函数对象以指定排序方式的写法非常基础,但其实在优先队列中指定排序方式的写法也并不困难。在sort中,我们传入一个函数指针,sort函数调用这个函数,获得它的返回值,从而得到元素之间的偏序。而在模板类中,由于需要在编译期就特化类,所以我们无法传入一个函数,而必须传入一个类。堆在排序时会调用其构造函数,获得构造函数的返回值,这整体上与我们给sort传参无异。
大多数情况下,我们可以使用STL提供的编译器函数库中的比较运算,例如小于是less,大于等于是greater_equal,等等。上面用于实现小根堆的greater源码如下:
template<typename _Tp>
struct greater : public binary_function<_Tp, _Tp, bool>
{
bool
operator()(const _Tp& __x, const _Tp& __y) const
{ return __x > __y; }
};
然而观察这一函数,它最终还是要调用具体类型的比较运算。那么如果我们给容器的类不具有偏序,或者我们需要特别指定偏序怎么办呢?下面给出一个实例。
例如,在图的搜索中我们需要存储点和它到源点的距离,那么我们的元素可能是这样的:
typename int Vertex;
typename int Distance;
typename pair<Vertex, Distance> Dest;
在Dijkstra算法中,用堆优化时我们需要建立边权的小根堆,那么就可以这样自建比较类型(我们知道自己要使用的类型,就不需要写成模板类了):
struct myGreater : public binary_function<Dest, Dest, bool>
{
bool operator() (const Dest &lhs, const Dest &rhs) const
{ return lhs.second > rhs.second; }
}
于是就可以这样建立基于边权的小根堆:
priority_queue<Dest, vector<Dest>, myGreater> myHeap;
七、Set及Multiset
7.1. 总览
set对应的ADT是集合:它支持元素的存储和查找,同时符合抽象意义上的集合要求——不允许出现重复元素。
7.2. 常见用法
set的一个重要用途就是排序同时去重。在BST家族中,理论表现最好的是Fibonacci-heap,但由于常数过大,实际表现最好的数据结构其实是set所采用的底层结构红黑树。如果说排序去重可以通过使用一个sort函数加手工来完成,那么需要支持插入和查找的题目呢?莫非我们要手写RBT吗?这时候,一个深受考验的set无疑是广大竞赛选手的福音。
当然,在更多的情况下,我们需要允许数据中出现重复的元素,那么可以使用multiset这种数据结构,它在其他地方与set无异,唯一的区别在于它允许重复元素的出现。
在容器中,find函数在找不到对象的时候一般会返回end,那么查找可以写作:
if (c.find(x) != c.end())
//do something...
八、Map
8.1. 总览
8.2. 常见用法
map和set非常类似,只不过它的数据是键值对而非一个单独的键,而键是唯一的。如果给它的用途举个例子,可以是存储源点到所有可达点的访问记录。
当然,同map一样,它也有允许键不唯一的版本,那就是multimap。本质上,multimap等价于multiset,其中Comp是自主实现的依据Key的比较类型。
也就是说,map和set和priority_queue一样,支持特化比较类型,特化的方式也是一样的。只不过实际使用的时候,不要忘记最后一个模板参数,那是用于生成元素空间的分配器。
九、总结
本文最后,给出一个表格以供检索,相比于cppreference的总结,这里只列出了竞赛中常用的一些操作及其复杂度。begin()和end()虽然较为常用,不过由于是全体容器必备的,所以不再列出。

这样,这篇文章也就基本结束了。可以看到,为了照顾特定的使用需求,本文对容器具体的实现未做过多探讨,反而对通常不太重视的迭代器部分做了一定的讲解。在竞赛中掌握这些内容,已经能够满足几乎全部的需求了。但在实际应用中,掌握这些内容甚至不足以通过一个大厂的面试。例如,deque的若是对容器原理有兴趣,可以找市面上评价较好的STL源码解读类书籍学习。

