分治策略------棋盘覆盖（ChessBoard）

棋盘覆盖原理

棋盘覆盖运用的是分治策略。

1.分治的技巧在于如何划分棋盘，使划分后的子棋盘的大小相同，并且每个子棋盘均包含一个特殊方格，从而将原问题分解为规模较小的棋盘覆盖问题。

2.k>0时，可将2^k×2k的棋盘划分为4个2^（k-1）×2（k-1）的子棋盘。这样划分后，由于原棋盘只有一个特殊方格，所以，这4个子棋盘中只有一个子棋盘包含该特殊方格，其余3个子棋盘中没有特殊方格。

3.为了将这3个没有特殊方格的子棋盘转化为特殊棋盘，以便采用递归方法求解，可以用一个L型骨牌覆盖这3个较小棋盘的会合处，从而将原问题转化为4个较小规模的棋盘覆盖问题。

4.递归地使用这种划分策略，直至将棋盘分割为1×1的子棋盘。

具体过程

1.首先定义一个2^n个行和列的棋盘，并在棋盘中标记一个小黑点。如图2.1所示（图2.1取n = 2时的一个特殊情况）。

2.将棋盘以2^(n-1)的模式分割。即可得到图2.2的情形。

3.分割以后即可看成四个相同的小棋盘，观察黑点在哪一个位置，并把不在的角落全部标记，如图2.3所示。

4.将棋盘进一步分割，如图2.4所示。然后识别每一小块是否含有已被标记的方块。然后继续分割，直到分割成一个2*2的小方格。

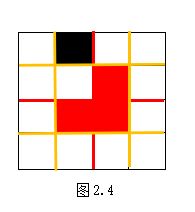
5.最后得到的是一个2*2的小方格，最后进行填充即可。

代码实现

// · x为特殊方格块的行标
// · y为特殊方格块的列标
// · tr为棋盘左上角的行标
// · tc为棋盘左上角的列标
// · size为棋盘的尺寸
void ChessBoard(int tr, int tc, int x, int y, int size){
    if(size == 1){
        return ;
    }
    int t = tile ++;         // L型骨牌号码 
    int s = size / 2;            // 分割棋盘
    // 判断特殊点是否在左上角
    if(x < tr + s && y < tc + s){
        ChessBoard(tr, tc, x, y, s); // 直接进入下一次分割
    }else{
        chessmap[tr + s - 1][tc + s - 1] = t; //赋值
        ChessBoard(tr, tc, tr + s - 1, tc + s - 1, s); // 下一次分割
    }
    // 判断特殊点是否在右上角
    if(x < tr + s && y >= tc + s){
        ChessBoard(tr, tc + s, x, y, s); // 直接进入下一次分割
    }else{
        chessmap[tr + s - 1][tc + s] = t; //赋值
        ChessBoard(tr, tc + s, tr + s - 1, tc + s, s); // 下一次分割
    }
    // 判断特殊点是否在左下角
    if(x >= tr + s && y < tc + s){
        ChessBoard(tr + s, tc, x, y, s); // 直接进入下一次分割
    }else{
        chessmap[tr + s][tc + s - 1] = t; //赋值
        ChessBoard(tr + s, tc, tr + s, tc + s - 1, s); // 下一次分割
    }
    // 判断特殊点是否在右下角
    if(x >= tr + s && y >= tc + s){
        ChessBoard(tr + s, tc + s, x, y, s); // 直接进入下一次分割
    }else{
        chessmap[tr + s][tc + s] = t; //赋值
        ChessBoard(tr + s, tc + s, tr + s, tc + s, s); // 下一次分割
    }
    return ;
}

具体实例

#include 
#include 
using namespace std;
const int MAX = 105;
int tile = 1; // 记L型骨牌号码
int chessmap[MAX][MAX]; // 定义棋盘
int n, a, b;
// · x为特殊方格块的行标
// · y为特殊方格块的列标
// · tr为棋盘左上角的行标
// · tc为棋盘左上角的列标
// · size为棋盘的尺寸
void ChessBoard(int tr, int tc, int x, int y, int size){
    if(size == 1){
        return ;
    }
    int t = tile ++;         // L型骨牌号码 
    int s = size / 2;            // 分割棋盘
    // 判断特殊点是否在左上角
    if(x < tr + s && y < tc + s){
        ChessBoard(tr, tc, x, y, s); // 直接进入下一次分割
    }else{
        chessmap[tr + s - 1][tc + s - 1] = t; //赋值
        ChessBoard(tr, tc, tr + s - 1, tc + s - 1, s); // 下一次分割
    }
    // 判断特殊点是否在右上角
    if(x < tr + s && y >= tc + s){
        ChessBoard(tr, tc + s, x, y, s); // 直接进入下一次分割
    }else{
        chessmap[tr + s - 1][tc + s] = t; //赋值
        ChessBoard(tr, tc + s, tr + s - 1, tc + s, s); // 下一次分割
    }
    // 判断特殊点是否在左下角
    if(x >= tr + s && y < tc + s){
        ChessBoard(tr + s, tc, x, y, s); // 直接进入下一次分割
    }else{
        chessmap[tr + s][tc + s - 1] = t; //赋值
        ChessBoard(tr + s, tc, tr + s, tc + s - 1, s); // 下一次分割
    }
    // 判断特殊点是否在右下角
    if(x >= tr + s && y >= tc + s){
        ChessBoard(tr + s, tc + s, x, y, s); // 直接进入下一次分割
    }else{
        chessmap[tr + s][tc + s] = t; //赋值
        ChessBoard(tr + s, tc + s, tr + s, tc + s, s); // 下一次分割
    }
    return ;
}
int main(){
    
    cin >> n >> a >> b;

    ChessBoard(0, 0, a, b, n);

    for(int i = 0; i < n; i ++){
        for(int j = 0; j < n; j ++){
            cout << setw(2) << setfill(' ') <<chessmap[i][j] << " ";
        }
        cout << endl;
    } 
    system("pause");
    return 0;
}

时间复杂度分析

设T(k)是算法所需要的时间，则T(k)满足如下方程：

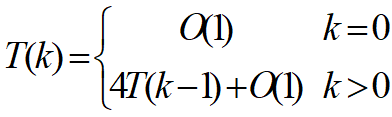
解此递归方程可得T(k) = O(4^k)。由于覆盖一个2^kx2^k棋盘所需要的L型骨牌个数为
（4^k- 1）/ 3。估该算法是一个在渐进意义下的最优算法。