决策树的理解及实现(小白版附代码)
前言
本文的代码部分均采用伪代码+代码的形式,帮助有些想挑战自己的小白同学可以自己通过伪代码敲出代码!
简介
决策树(Decision Tree)是一种十分常用的分类方法。作为一种有监督学习,它对特征属性和样本标签之间的映射关系进行建模。相对于K-近邻算法,决策树的主要优势在于数据形式非常容易理解。而决策树之所以称为树,是因为其处理数据的过程可以用树来表示。理论总是那么难以理解,那我们直接上例子吧
一个例子
表1的数据包括5个样本,其特征分别为A,B,样本标签用L表示。特征值和样本标签都只有两种取值:是,否。

现在,我们先尝试用两个特征来对样本进行划分,并用树结构表示:
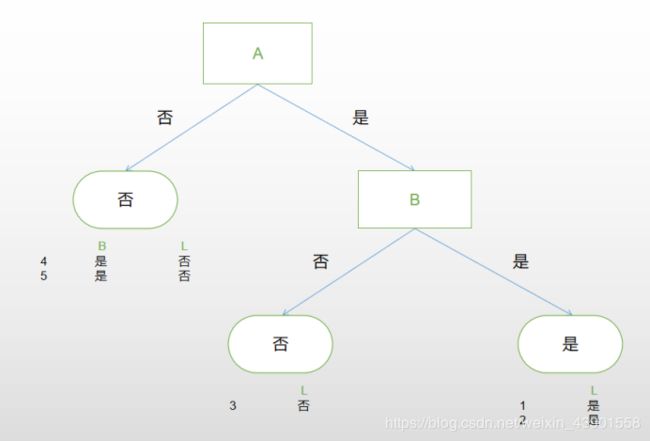
从图1中我们可以看出:
当特征A的值为否时(即样本4,5),样本标签均为否。因此我们可以预测当A为否时,无论B为何值,样本标签为否
当特征A的值为是时(即样本1,2,3),此时标签不太好分了(有是,也有否),因此我们再用B来进行划分:
当A为是,B为否时(即样本3),样本标签均为否。因此我们可以预测当A为是,B为否时,样本标签为否。
当A为是,B为是时(即样本1,2),样本标签均为是。因此我们可以预测当A为是,B为是时,样本标签为是。
此时我们就将样本都分完了,如果再给我们一组特征值,我们能够轻松地通过特征值,找到“对应”的样本标签了。是不是很简洁明了?
现在探讨一个问题。显而易见,数据集有多个特征,因而也有多种划分方式(比如对于表1我们也可以先对B进行划分),划分数据集的大原则是:把无序的数据变得更加有序。而哪种数据划分方式是最好的数据划分呢?接下来我们引入熵和信息增益的概念。
熵
不要被这个很学术的名词吓到了哈~其实,只要你了解了这个名词之后,你就可以…拿它去装逼了。
熵这个名字起源于信息论之父克劳德·香农,据说在香农写完信息论之后,冯·诺伊曼建议使用“熵”这个术语,因为大家都不知道它是什么意思。
我的理解是,熵就是信息的不确定性。比如说,一个房间如果全部是口罩,那么它的信息量是很低的,而另一个房间里既有口罩,也有防护服,消毒液等等,我们就说它信息量较大。换言之,可能值越多,信息越不确定,熵越大。给出计算熵的公式:
![]()
其中P(xi)为可能值为i的概率,n为可能值的数目。举个例子,对于表1的样本标签,共有两种可能值,其中值为’是’的概率是0.4,值为’否’的概率是0.6,因此其熵为:-0.4log(0.4)-0.6log(0.6) = 0.97
下面贴出计算熵的伪代码:
for 实例 in dataSet:
建立key值为样本标签值,value值为标签值出现的次数的字典
通过每个实例更新该字典
for key in 字典:
计算每个标签出现的频率
更新香农熵
返回香农熵
代码如下:
def calcShannonEnt(dataSet):
numEntries = len(dataSet) # 数据集一共有多少个实例
labelCounts = {} # 定义一个字典,key为标签的可能值,value为该可能值的个数
for featVec in dataSet:
currentLabel = featVec[-1]
if currentLabel not in labelCounts.keys(): # 如果现在字典中没有该可能值,则初始化其value为0
labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1
shannonEnt = 0.0 # 初始化香农熵为0
for key in labelCounts:
prob = float(labelCounts[key])/numEntries
shannonEnt -= prob * log(prob, 2) # 计算香农熵
return shannonEnt
划分数据集
求得数据集的熵之后,我们就要通过特征的划分,来降低数据集的熵,这个降低的值,就是信息增益。信息增益的计算公式为(这个公式是我为了解释清楚而自己定义的,没有任何来历的):
![]()
其中n为该特征的可能值个数(即数据集被该特征划分成了多少块),Pi为第i块数据子集中的实例占整个数据集的比例,Hi为第i块数据子集的信息熵。所以,我们之前所要找的最好的划分方式,就是用信息增益最大的特征来进行划分(这里假设我们已经找到这个特征啦)。
划分数据集的伪代码如下:
# 函数参数为数据集dataSet,划分数据集的特征A, 划分后这一块数据子集对应的特征值V
创建空列表r
for 实例 in dataSet:
if 该实例的特征A的值为V:
将该实例的特征A去掉后添加到r中
返回r
代码如下:
def splitDataSet(dataSet, axis, value): # 输入参数分别为:待划分的数据集,划分数据集的特征,划分后这一块数据子集对应的特征值
retDataSet = [] # 建立新的list对象,存储划分后的数据子集
for featVec in dataSet: # 遍历数据集,一旦发现符合要求的实例,则将其元素抽取,并添加到新建的列表中
if featVec[axis] == value:
reducedFeatVec = featVec[:axis]
reducedFeatVec.extend(featVec[axis+1:])
retDataSet.append(reducedFeatVec)
return retDataSet
接下来我们将遍历整个数据集,循环计算香农熵和splitDataSet()函数,找到最好的划分方式,其伪代码如下:
计算原始香农熵
for 每个特征:
for 该特征的每个特征值:
用该特征值划分数据集
求得划分后数据子集的信息熵之和
求得该特征的信息增益
返回信息增益最大的特征
代码如下:
def chooseBestFeatureToSplit(dataSet):
numFeatures = len(dataSet[0]) - 1
baseEntropy = calcShannonEnt(dataSet) # 计算整个数据集的原始香农熵
bestInfoGain = 0.0
bestFeature = -1 # 初始化最大信息增益和最佳特征
for i in range(numFeatures): # 遍历每个特征
featList = [example[i] for example in dataSet]
uniqueVals = set(featList) # 集合(set)数据类型,得到featList中不重复的值
newEntropy = 0.0
for value in uniqueVals: # 遍历当前特征中的所有唯一属性值,对每个特征值都划分一次数据集
subDataSet = splitDataSet(dataSet, i, value)
prob = len(subDataSet)/float(len(dataSet))
newEntropy += prob * calcShannonEnt(subDataSet)
infoGain = baseEntropy - newEntropy # 计算当前特征的信息增益
if infoGain > bestInfoGain :
bestInfoGain = infoGain
bestFeature = i # 比较所有特征的信息增益,返回最好划分的特征索引值
return bestFeature
递归构建决策树
目前我们已经了解了从数据集构造决策树算法所需要的子功能模块,其工作原理为:
得到原始数据集,然后基于最好的特征划分数据集,由于特征的值可能多余两个,因此可能存在大于两个分支的数据集划分(即一个结点可能有大于两个子结点)。
第一次划分后,数据将被向下传递到树分支的下一个结点,在这个结点上,如果该数据子集的标签不完全一样,我们可以通过另一个特征再次划分数据,因此我们可以采用递归的原则来处理。
递归结束的条件是:程序遍历完所有特征,或者每个叶子结点的数据子集都有相同的标签。当然,还有一种情况,所有特征都被“用完”了,但样本标签依然不是唯一的,此时,我们通常会采用取多数的方法决定该叶子结点的标签。
取多数的伪代码如下:
# 函数参数为数据子集中标签的列表
建立一个字典,key为标签值,value为数据子集中标签值为key的个数
for 字典中的key:
更新字典
根据字典中的value对字典进行排序,返回出现最多的标签
代码如下:
def majorityCnt(classList):
classCount = {} # 建立一个字典,key为标签值,value为数据子集中标签值为key的个数
for vote in classList:
if vote not in classCount.keys():classCount[vote] = 0
classCount[vote] += 1
sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)
# .items()将字典分解为形式为([key,value], ...)的元组列表,运算符模块的itemgetter方法按第二个元素的次序对元组进行排序。返回出现次数最多的标签名称
return sortedClassCount
如今我们已经“万事俱备,只欠东风”。而最后一步,就是建树了。
给出建树的伪代码:
#函数参数为数据集dataSet和特征列表labels
if 标签完全相同:
返回标签值
if 遍历完特征:
调用majorityCnt,将其返回值作为返回值
调用chooseBestFeatureToSplit,找到最佳特征b
以b为key建立一个字典myTree
删除labels中的特征b
for 特征b的每一个不重复值value:
myTree[b]的键值为 递归调用该函数(其参数是什么?)
return myTree
下面直接贴上完整的代码吧
from math import log
import operator
def majorityCnt(classList):
classCount = {} # 建立一个字典,key为标签值,value为数据子集中标签值为key的个数
for vote in classList:
if vote not in classCount.keys():classCount[vote] = 0
classCount[vote] += 1
sortedClassCount = sorted(classCount.items(), key=operator.itemgetter(1), reverse=True)
# .items()将字典分解为形式为([key,value], ...)的元组列表,运算符模块的itemgetter方法按第二个元素的次序对元组进行排序
return sortedClassCount
def calcShannonEnt(dataSet):
numEntries = len(dataSet) # 数据集一共有多少个实例
labelCounts = {} # 定义一个字典,key为标签的可能值,value为该可能值的个数
for featVec in dataSet:
currentLabel = featVec[-1]
if currentLabel not in labelCounts.keys(): # 如果现在字典中没有该可能值,则初始化其value为0
labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1
shannonEnt = 0.0 # 初始化香农熵为0
for key in labelCounts:
prob = float(labelCounts[key])/numEntries
shannonEnt -= prob * log(prob, 2) # 计算香农熵
return shannonEnt
def createDataSet():
dataSet = [[1, 1, 'yes'],
[1, 1, 'yes'],
[1, 0, 'no'],
[0, 1, 'no'],
[0, 1, 'no']]
label = ['no surfacing', 'flippers']
return dataSet, label
def splitDataSet(dataSet, axis, value): # 输入参数分别为:待划分的数据集,划分数据集的特征,划分后这一块数据子集对应的特征值
retDataSet = [] # 建立新的list对象,存储划分后的数据子集
for featVec in dataSet: # 遍历数据集,一旦发现符合要求的实例,则将其元素抽取,并添加到新建的列表中
if featVec[axis] == value:
reducedFeatVec = featVec[:axis]
reducedFeatVec.extend(featVec[axis+1:])
retDataSet.append(reducedFeatVec)
return retDataSet
def chooseBestFeatureToSplit(dataSet):
numFeatures = len(dataSet[0]) - 1
baseEntropy = calcShannonEnt(dataSet) # 计算整个数据集的原始香农熵
bestInfoGain = 0.0
bestFeature = -1 # 初始化最大信息增益和最佳特征
for i in range(numFeatures): # 遍历每个特征
featList = [example[i] for example in dataSet]
uniqueVals = set(featList) # 集合(set)数据类型,得到featList中不重复的值
newEntropy = 0.0
for value in uniqueVals: # 遍历当前特征中的所有唯一属性值,对每个特征值都划分一次数据集
subDataSet = splitDataSet(dataSet, i, value)
prob = len(subDataSet)/float(len(dataSet))
newEntropy += prob * calcShannonEnt(subDataSet)
infoGain = baseEntropy - newEntropy # 计算当前特征的信息增益
if infoGain > bestInfoGain :
bestInfoGain = infoGain
bestFeature = i # 比较所有特征的信息增益,返回最好划分的特征索引值
return bestFeature
def createTree(dataSet, labels):
classList = [example[-1] for example in dataSet]
if classList.count(classList[0]) == len(classList):
return classList[0]
if len(dataSet[0]) == 1:
return majorityCnt(classList)
bestFeat = chooseBestFeatureToSplit(dataSet)
bestFeatLabel = labels[bestFeat]
myTree = {bestFeatLabel:{}}
del(labels[bestFeat])
featValues = [example[bestFeat] for example in dataSet]
uniqueVals = set(featValues)
for value in uniqueVals:
subLabels = labels[:]
myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels)
return myTree
myDat, labels = createDataSet()
myTree = createTree(myDat, labels)
print(myTree)
结果如下
{'no surfacing': {0: 'no', 1: {'flippers': {0: 'no', 1: 'yes'}}}}
结语
本文的例子和代码均来自《机器学习实战》第三章
第一次写博客,虽然主要参(zhao)考(ban)了《机器学习实战》,但还是费了一番工夫,其实写博客的过程也是加深自己理解的过程。
之后会努力把数据挖掘的十大算法都陆续写完,这样也好打发宅在家的这段时间。
欢迎大家收藏,但更欢迎大家批评指正哈哈!第一次肯定很多疏漏,包括很多功能我都不太会…谢谢大家!