算法&数据结构学习(2) 剑指offer刷题笔记(1)
算法的世界是真的奇妙,有趣,深深不能自拔!!!前段时间刚学习算法与数据结构的时候都是一脸懵逼,看啥啥不懂,软磨硬泡了两个月,leetcode也刷了两三百题了,剑指Offer也过了一遍,今日起再刷第二遍,同时也对学习进行记录,以便以后自己查看当做笔记!!!
面试题03. 数组中重复的数字

解法1:哈希(C++中set或者unordered_set)
class Solution {
public:
int findRepeatNumber(vector<int>& nums) {
//法1:哈希
unordered_set<int> table;
for(auto n:nums)
{
if(table.count(n)) return n;
table.insert(n);
}
return -1;
}
};
解法2:原地置换
思路:由于原数组都是在0到n-1,因此如果没有重复数字,置换完成以后,所有数字都应该对应于下标。因此只要遍历数组进行原地置换,遇到重复数字即可返回。
class Solution {
public:
int findRepeatNumber(vector<int>& nums) {
//法2:原地置换
int tmp;
for(int i=0; i<nums.size(); ++i)
{
while(nums[i]!=i)
{
if(nums[i]==nums[nums[i]]) return nums[i];//遇到重复数字返回
tmp = nums[i];
nums[i] = nums[tmp];
nums[tmp] = tmp;
}
}
return -1;
}
};
面试题04. 二维数组中的查找
class Solution {
public:
bool findNumberIn2DArray(vector<vector<int>>& matrix, int target) {
//思路:本题的二维数组比较特殊,因此可以考虑使用其相关性质
//容易看出的一个性质:不论是在左下角或右上角开始,这个矩阵和二叉搜索树有一样的性质
//因此遍历的时候与二分查找类似,可以避免如左上角暴力遍历的额外开销
int row = matrix.size()-1, col = 0;
while(row>=0 && col < matrix[0].size())//从左下角开始
{
if(matrix[row][col]<target)
++col;
else if(matrix[row][col]>target)
--row;
else
return true;
}
return false;
}
};
面试题05. 替换空格
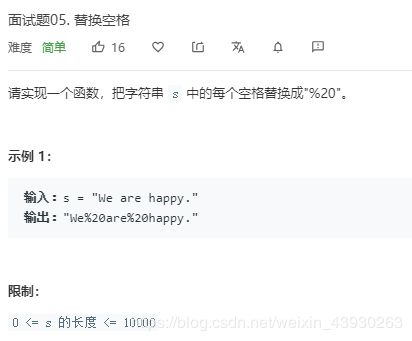
思路比较简单:创建新的字符串,然后对原字符串进行遍历,遇到空格则替换为%20,否则直接复制过去即可。
class Solution {
public:
string replaceSpace(string s) {
//思路:字符数组
string res;
for(auto ch:s)
if(ch==' ')
res.append("%20");
else
res.push_back(ch);
return res;
}
};
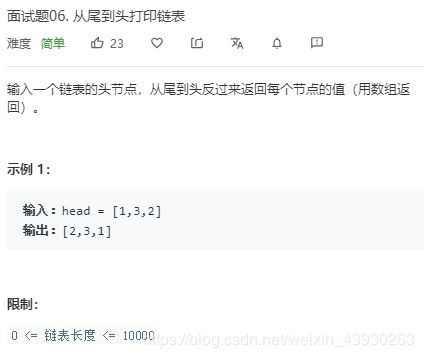
面试题06. 从尾到头打印链表
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode(int x) : val(x), next(NULL) {}
* };
*/
class Solution {
public:
vector<int> reversePrint(ListNode* head) {
//法1:递归法
vector<int> res;
recur(head,res);
return res;
}
void recur(ListNode* head, vector<int>& res)
{
if(!head) return;
recur(head->next,res);
res.push_back(head->val);
}
};
法2:辅助栈(数据结构标准思想,逆序输出首先肯定想到栈,此题不例外)
class Solution {
public:
vector<int> reversePrint(ListNode* head) {
//法2:辅助栈
stack<int> s;
vector<int> res;
while(head)
{
s.push(head->val);
head=head->next;
}
while(!s.empty())
{
res.push_back(s.top());
s.pop();
}
return res;
}
};
法3:c++翻转函数,直接顺序遍历链表,再调用库函数翻转结果
class Solution {
public:
vector<int> reversePrint(ListNode* head) {
//c++翻转函数
vector<int> res;
while(head)
{
res.push_back(head->val);
head=head->next;
}
reverse(res.begin(),res.end());
return res;
}
};
面试题07. 重建二叉树

解题思路:在树的三种前、中、后序遍历中,前序/后序+中序遍历都可以确定唯一的一棵二叉树,即建树的基础。
本题中,前序和中序遍历有如下特点:
1、前序遍历的左起第一个元素一定是根节点,即我们就可以构建root;
2、中序遍历中根节点左侧的元素就是左子树,右侧元素就是右子树,因此就有左子树节点个数:left = index - lin;
3、前序遍历的结点分布:[根节点,左子树,右子树];
4、根据前一步确定的左子树个数,可以确定前序中左子树节点和右子树节点的范围;
5、由此即可递归建树:
左子树:root->left = build(前序遍历左子树范围,中序遍历左子树范围)
右子树:root->right = build(前序遍历右子树范围,中序遍历右子树范围)
6、递归返回每一层构建的根节点root即可;
代码如下:
class Solution {
public:
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
return build(preorder,0,inorder.size()-1, inorder,0,inorder.size()-1);
}
TreeNode* build(vector<int>& pre,int lpre, int rpre, vector<int>& in, int lin, int rin)
{
if(lpre>rpre || lin>rin) return nullptr;
TreeNode* root = new TreeNode(pre[lpre]);//前序遍历的左元素一定是树根
int index = lin;
while(index<=rin && in[index]!=pre[lpre])//从中序遍历找出根节点下标
index++;
int left = index - lin;//左子树个数
//递归构建左子树
root->left = build(pre, lpre+1, lpre+left, in, lin, rin-1);
//递归构建右子树
root->right = build(pre, lpre+left+1, rpre, in, index+1, rin);
return root;
}
};
面试题09. 用两个栈实现队列
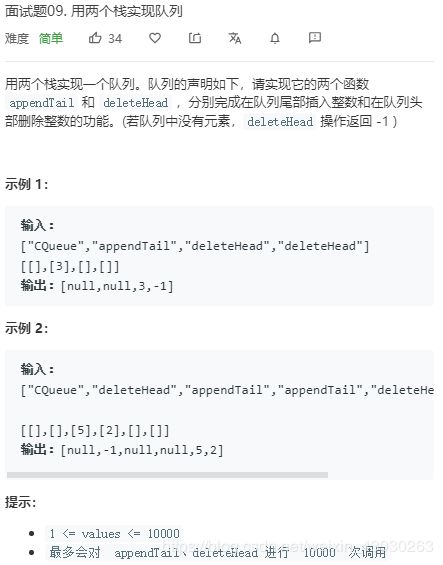
思路:双栈实现队列的思路,栈s1用作入队的栈,当执行deleteHead操作时,先判断s2辅助栈中是否为空,如果空,则将s1中的元素逐个移至S2,即相当于再一次翻转元素,此时s2中的元素已经按照入栈s1的先后顺序从栈顶至栈底排列在s2中,此后每次入队操作直接入s1,出队则先判断s2是否空,不空直接弹出s2栈顶元素,如果为空则重复s1到s2的操作。如果两个都空直接返回-1。
class CQueue {
public:
CQueue() {
}
void appendTail(int value) {
s1.push(value);
}
int deleteHead() {
if(s1.empty() && s2.empty()) return -1;
int deletenum;
if(s2.empty())
while(!s1.empty())
{
s2.push(s1.top());
s1.pop();
}
deletenum = s2.top();
s2.pop();
return deletenum;
}
private:
stack<int> s1;
stack<int> s2;
};
(构建二叉树补充)106. 从中序与后序遍历序列构造二叉树
剑指offer题库中构建二叉树是由前序和中序进行构建,而正如前序和中序一样,后序和中序构建的二叉树思路如初一整。
class Solution {
public:
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
return buildTree(inorder,0,inorder.size()-1, postorder,0,inorder.size()-1);
}
TreeNode* buildTree(vector<int>& in, int lin, int rin, vector<int>& post, int lpost, int rpost)
{
if(lin>rin || lpost>rpost) return nullptr;
TreeNode* root = new TreeNode(post[rpost]);//构建根节点
int index = rin;
while(index>=lin && in[index]!=post[rpost])
--index;
int right = rin-index;
//递归构建左子树
root->left = buildTree(in,lin,index-1,post,lpost,rpost-right-1);
root->right = buildTree(in,index+1,rin,post,rpost-right,rpost-1);
return root;
}
};
今日分笔记圆满完成!!!明日继续,冲冲冲!!!