本文始发于个人公众号:TechFlow,原创不易,求个关注
今天是机器学习专题的第20篇文章,我们来看看FP-growth算法。
这个算法挺冷门的,至少比Apriori算法冷门。很多数据挖掘的教材还会提一提Apriori,但是提到FP-growth的相对要少很多。原因也简单,因为从功能的角度上来说,FP-growth和Apriori基本一样,相当于Apriori的性能优化版本。
但不得不说有时候优化是一件很尴尬的事,因为优化意味着性能要求很高。但是反过来说,对于性能有着更高要求的应用场景,无论是企业也好,还是学术研究也罢,现在早就有了更好的选择,完全可以用更强大的算法和模型,没必要用这么个古老算法的优化版。对于那些性能要求不高的场景,简单的Apriori也就够了,优化的必要也不是很大。
但是不管这个算法命运如何,至少从原理和思路理念上来说的确有为人称道的部分。下面我们就来看看它的具体原理吧。
FP-growth与FP-tree
FP-growth的核心价值在于加速,在之前介绍的Apriori算法当中,我们每一次从候选集当中筛选出频繁项集的时候,都需要扫描一遍全量的数据库来计算支持度,显然这个开销是很大的,尤其是我们数据量很大的时候。
FP-growth的精髓是构建一棵FP-tree,它只会扫描完整的数据集两次,因此整体运行的速度显然会比Apriori快得多。之所以能做到这么快,是因为FP-growth算法对于数据的挖掘并不是针对全量数据集的,而只针对FP-tree上的数据,因此这样可以省略掉很大一部分数据,从而节省下许多计算资源。
从这里我们可以看出,FP-tree是整个算法的精髓。在我们介绍整个树的构建方法以及一些细节之前,我们先来看下FP这两个字母的含义。相信很多同学从一开始的时候就开始迷惑了,其实FP这两个字母是frequent pattern的缩写,翻译过来是频繁模式,其实也可以理解成频繁项,说白了,FP-tree这棵树上只会存储频繁项的数据,我们每次挖掘频繁项集和关联规则都是基于FP-tree,这也就过滤了不频繁的数据。
这是一棵生成好的FP-tree,我们先来看一下它的样子,再来详细解读其中的细节和原理。

头指针表
上图这个结构初看会觉得很混乱,完全不知道应该怎么理解。这是很正常的,但如果我们把上图拆开,可以分成两个部分,左边的部分是一个链表,右边是一棵树。只不过左边的链表指到了右边的树上,所以整体看起来有些复杂。
我们先忽略右侧的树的部分,以及指针表和树之间关联的指针,单纯地来看一下左侧的头指针表。仅仅看这一部分就简单多了,它其实是一个单频繁项的集合。
前面我们提到我们在使用FP-growth算法的过程当中,一共只需要遍历两次数据集。其中第一次遍历数据集就在这里,我们首先遍历了一遍数据集,求出了所有元素出现的次数。然后根据阈值过滤掉不频繁的元素,保留下来的结果就是单个频繁项的集合。
这里的逻辑非常简单,只有两件事,第一件事是统计每个单独的项出现的次数,第二件事是根据阈值将不频繁的项过滤掉。
def filter_unfreq_items(dataset, min_freq):
data_dict = defaultdict(int)
# 统计每一项出现的次数
for trans in dataset:
for item in trans:
data_dict[item] += 1
# 根据阈值过滤
ret = {}
for k, v in data_dict.items():
if v >= min_freq:
ret[k] = v
return ret
通过这个方法,我们就生成了头指针表里的数据。之后我们要在建立FP-tree的过程当中将这份数据转化成链表,也就是左边的头指针表。虽然我们还不了解建树的原理,但至少我们可以把dict转化成指针表,这个逻辑非常简单,说白了我们只需要在dict的value当中增加一个引用即可。
def transform_to_header_table(data_dict):
return {k: [v, None] for k, v in data_dict.items()}
这里的None要存的就是链表下一个位置的引用,只是目前我们只有链表头,所以全部设置为None。
建立FP-tree
我们有了头指针表的数据,也就是高频的单个元素的数据之后,显然要将它用起来。很明显,我们可以用它来过滤整个数据集,过滤掉其中低频的元素。
其实本质上来说FP-tree的构建过程,其实就是一个将过滤之后的结果插入到树上的过程。后面的事情后面再说,我们首先来看过滤。
单纯的过滤当然非常简单,我们只需要判断数据集中的元素是否在头指针表中出现即可。但是不仅如此,由于我们之后想要将它插入到树中。这里利用了huffman树的思想,我们希望频次越高的元素存放的位置距离根节点越近。频次越低的离根节点越远,从而优化我们查询的效率。要做到这点,需要我们对数据进行排序。
我们来实现这部分内容,这部分内容分为两块,第一块是根据头指针表进行过滤,第二块是根据头指针表中出现的频次进行排序。
def rank_by_header(data, header_dict):
rank_dict = {}
for item in data:
# 如果元素是高频的则保留,否则则丢弃
if item in header_dict:
rank_dict[item] = header_dict[item]
# 对元素按照整体出现的频次排序
item_list = sorted(rank_dict.items(), lambda x: x[1], reverse=True)
return [i[0] for i in item_list]
有了这份数据之后,我们距离建树只有一步之遥。FP-tree的构建刚才也提到过,非常简单粗暴,就是将元素按照出现的频次进行排序之后从树根开始依次插入。在插入的过程当中,对路径上的节点进行更新,我这么说肯定很费解,但是看一张图就肯定明白了:

一开始的时候树为空,什么也没有,接着插入第一条数据{r, z}。由于z出现的次数大于r,所以先插入z再插入r,之后插入了一条{z,x,y,s,t},同样是按照整体出现的频次排序的。由于z已经插入了,所以我们将它出现的次数更新成2,之后发现没有重复的元素,那么就构建出一条新的分支。
本质上来说就是按照频次排序之后,由浅到深依次插入,如果相同的元素之前已经出现过了,那么就更新它出现的次数。
这个逻辑应该很好理解,在我们实现逻辑之前,我们先来创建树节点的类。
class Node:
def __init__(self, item, freq, father):
self.item = item
self.freq = freq
# 父节点指针
self.father = father
# 定义指针
self.ptr = None
# 孩子节点,用dict存储,方便根据item查找
self.children = {}
# 更新频次
def update_freq(self):
self.freq += 1
# 新增孩子
def add_child(self, node):
self.children[node.item] = node
这个类我们只需要看代码就好了,应该完全没有难度,当然如果你愿意你也可以给它加上一个可视化方法用来debug。但老实说树结构单凭打印很难显示得很清楚,所以我就不加了。
树节点的定义写好了之后,接下来就到了最重要的实现更新FP-tree的环节了。其实如果对上面的逻辑都理解了,这部分代码也非常简单,我们只需要套用刚才的代码将生成的数据按照顺序插入进树上即可。
这种在树上传入一个序列依次插入的做法非常常见,在很多数据结构当中有类似的操作,最经典的就是Trie树了。如果你学过,会发现这个插入操作真的和Trie几乎一模一样,如果你没学过,也没有关系,这也不难理解。
def create_FP_tree(dataset, min_freq=3):
header_dict = filter_unfreq_items(dataset, min_freq)
root = Node('Null', 0, None)
for data in dataset:
# 根据整体出现次数进行排序
item_list = rank_by_header(data, header_dict)
print(item_list)
head = root
# 按照排序顺序依次往树上插入
for item in item_list:
if item in head.children:
head = head.children[item]
else:
new_node = Node(item, 0, head)
head.add_child(new_node)
head = new_node
head.update_freq()
return root
更新头指针表
FP-tree已经完成了,接下来我们要把更新头指针表的逻辑加上,使得对于每一个项来说,我们都可以根据头指针表找到这个元素在FP-tree上所有的位置。
我们仔细观察一下上面的那张图,我们选择其中的一条链路进行高亮:
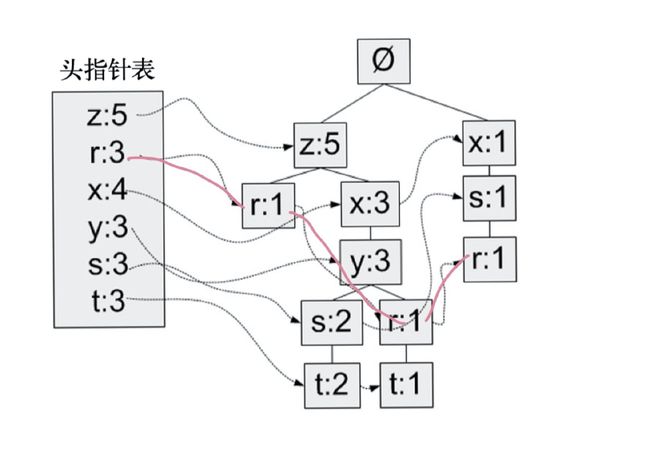
从上图当中我们会发现,头指针表的作用就是建立一个链表,将元素所有出现的位置全部串联起来。
那么什么情况下我们需要向这个链表当中添加值呢?
稍微分析一下就会发现,其实就是我们在树上创建新节点的时候。想通了这点就很简单了,我们只需要在上面的代码当中增加几行,使得在树上创建新的节点的时候,用同样的值更新一下头指针链表。
def create_FP_tree(dataset, min_freq=3):
header_dict = filter_unfreq_items(dataset, min_freq)
root = Node('Null', 0, None)
for data in dataset:
# 根据整体出现次数进行排序
item_list = rank_by_header(data, header_dict)
print(item_list)
head = root
# 按照排序顺序依次往树上插入
for item in item_list:
if item in head.children:
head = head.children[item]
else:
new_node = Node(item, 0, head)
head.add_child(new_node)
# 头指针指向的位置为空,那么我们直接让头指针指向当前位置
if head_table[item][1] is None:
head_table[item][1] = new_node
else:
# 否则的话,我们将当前元素添加到链表的末尾
insert_table(head_table[item][1], new_node)
head = new_node
head.update_freq()
return root
这里添加到末尾的操作,我们可以再创建一个dict来维护头指针表的末尾节点,但我这里偷懒了一下,就用最简单的办法,先遍历到链表的结尾,再进行添加:
def insert_table(head_node, node):
while head_node.ptr is not None:
head_node = head_node.ptr
head_node.ptr = node
通过FP-tree快速查找数据
现在,我们已经完整实现了FP-tree的构建,接下来就到了重头戏,也就是频繁项集的挖掘。我们有了这棵FP-tree之后应该怎么用呢?
如果我们仔细观察一下FP-tree的话,会发现这棵树其实是数据的浓缩。可以认为是之前完整的数据集去除了非频繁的元素之后提炼得到的数据。根据APriori算法的原理,我们接下来要做的就是用长度为1的频繁项集去构建长度为2的频繁项集,以此类推,直到找出所有的频繁项集为止。
但是在FP-growth算法当中,我们对这个逻辑稍稍做了一点点修正,我们每次固定一个元素,查找所有它构成的频繁项集。我们要查找频繁项集,首先需要获取数据集,原始的数据包含了太多无关的信息,我们已经用不到了,我们可以通过FP-tree高效地获取我们需要的数据。
由于我们之前在插入FP-tree的时候,是严格按照元素出现的次数排序的,出现频次高的元素放置的位置越高。这样树上某一个链路在数据集中出现的次数,就等于链路中最底层的节点的数字。
我们来看个例子:
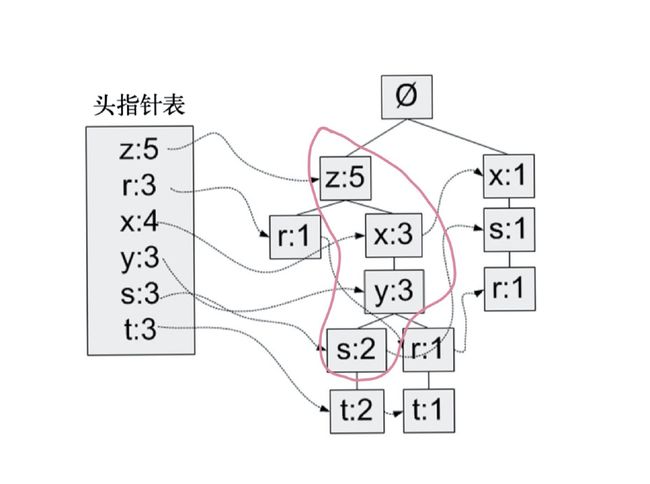
红框当中s的位置最低,所以整个链路上{z, x, y, s}在整个数据集当中出现的次数就是2,那么我们确定了s之后,通过向上FP-tree,就可以还原出所有包含s的频繁项构成的数据。
我们首先实现一个辅助方法,用来向上遍历整个链路所有的元素:
def up_forward(node):
path = []
while node.father is not None:
path.append(node)
node = node.father
# 过滤树根
return path
第二个辅助方法是固定某个元素之后,还原所有这个元素的数据。要还原所有数据,只拿到一个节点是不够的,我们需要知道这个元素在FP-tree上所有出现的位置。这个时候就需要用到头指针表了,利用头指针表,我们可以找到所有元素在FP-tree中的位置,我们只需要调用上面的方法,就可以还原出数据集了。
这段逻辑同样并不困难,其实就是遍历一个链表,然后再调用上面向上遍历树的方法,获取所有的数据。
def regenerate_dataset(head_table, item):
dataset = {}
if item not in head_table:
return dataset
# 通过head_table找到链表的起始位置
node = head_table[item][1]
# 遍历链表
while node is not None:
# 对链表中的每个位置,调用up_forward,获取FP-tree上的数据
path = up_forward(node)
if len(path) > 1:
# 将元素的set作为key
# 这里去掉了item,为了使得新构建的数据当中没有item
# 从而挖掘出以含有item为前提的新的频繁项
dataset[frozenset(path[1:])] = node.freq
node = node.ptr
# 将kv格式的数据还原成数组形式
ret = []
for k, v in dataset.items():
for i in range(v):
ret.append(list(k))
return ret
递归建树,挖掘频繁项集
到这里,我们对FP-tree应该有一个比较清晰的认识了,它的功能就是可以快速地查找某些元素组合的集合的频次,因为相同元素构成的集合都被存储在同一条树链上了。
那么我们怎么根据FP-tree来挖掘频繁项集呢?
这里才是真正的算法的精髓。
我们还是看下上面的例子:
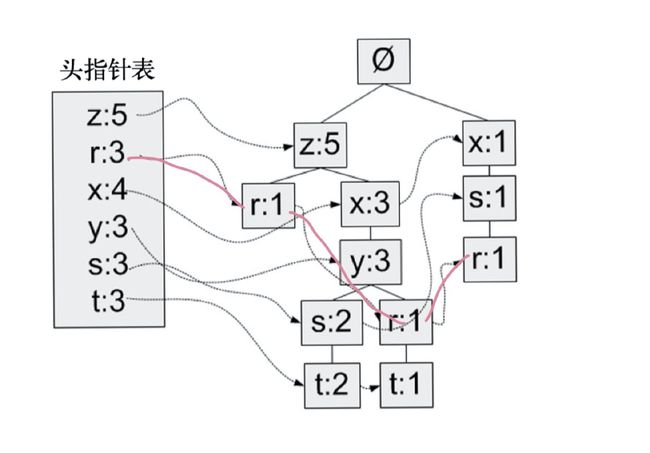
我们假设我们固定的元素是r,我们通过FP-tree可以快速找到和r共同出现的频繁项有z,x,y,s。通过刚才上面的方法,我们可以得到一个新的必须包含r和频繁项的新的数据集。我们把r从这份数据当中去除,然后对剩下的数据构建新的FP-tree,如果新的FP-tree当中还有其他元素,那么这个元素必然可以和r构成二元的频繁项集。假设这个元素是x,那么我们继续重复上面的操作,再将x从数据中去除,再次构建FP-tree来挖掘包含x和r的三元频繁项集,直到构成的FP-tree当中没有元素了为止。
这就成了一个递归调用的过程,也就是说FP-tree本身并不能挖掘频繁项集,只能挖掘频繁项。但是我们可以人为加上前提条件,当我们以必须包含x的数据为前提挖掘出来的频繁项,其实就是包含x的二元频繁项集。我们加上的前提越来越多,也就是挖掘的频繁项集的元素越来越多。
如果你还有点蒙,没有关系,我们来看下代码:
def mine_freq_lists(root, head_table, min_freq, base, freq_lists):
# 对head_table排序,按照频次从小到大排
frequents = [i[0] for i in sorted(head_table.items(), key=lambda x: x[0])]
for freq in frequents:
# base是被列为前提的频繁项集
new_base = base.copy()
# 把当前元素加入频繁项集
new_base.add(freq)
# 加入答案
freq_lists.append(new_base)
# 通过FP-tree获取当前频繁项集(new_base)为基础的数据
new_dataset = regenerate_dataset(head_table, freq)
# 生成新的head_table
new_head_table = transform_to_header_table(filter_unfreq_items(new_dataset, min_freq))
# 如果为空,说明没有更长的频繁项集了
if len(new_head_table) > 0:
# 如果还有,就构建新的FP-tree
new_root = create_FP_tree(new_dataset, new_head_table, min_freq)
# 递归挖掘
mine_freq_lists(new_root, new_head_table, min_freq, new_base, freq_lists)
if __name__ == "__main__":
dataset = create_dataset()
data_dict = filter_unfreq_items(dataset, 3)
head_table = transform_to_header_table(data_dict)
root = create_FP_tree(dataset, head_table, 3)
data = regenerate_dataset(head_table, 'r')
freq_lists = []
mine_freq_lists(root, head_table, 3, set([]), freq_lists)
结尾
到这里,整个FP-growth挖掘频繁项集的算法就结束了,相比于Apriori,它的技术细节要多得多,如果初学者觉得不太好理解,这也是正常的,可以抓大放小,先从核心思路开始理解。
Apriori的核心思路是用两个长度为l的频繁项集去构建长度为l+1的频繁项集,而FP-growth则稍有不同。它是将一个长度为l的频繁项集作为前提,筛选出包含这个频繁项集的数据集。用这个数据集构建新的FP-tree,从这个FP-tree当中寻找新的频繁项。如果能找到,那么说明它可以和长度为l的频繁项集构成长度为l+1的频繁项集。然后,我们就重复这个过程。
这个核心思路理解了,怎么构建FP-tree,怎么维护头指针表都是很简单的问题了。
各位看官大人,请关注我吧~
