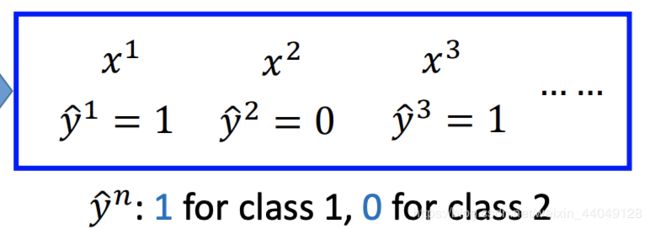李宏毅机器学习（四）

此篇博文是基于李宏毅老师此视频的学习总结。此部分主要介绍，Logistic Regression模型。

一、课程部分内容记录

(1) Logistics Regression和Linear Regression对比

	Logistics Regression	Linear Regression
Step 1：	$f_{w,b}(x)=\sigma ({\sum }_i{w}_i{x}_j+b)$ Output：value between 0 and 1	$f_{w,b}(x)={\sum }_i{w}_i{x}_j+b$ Output：any value
Step 2：	Training data:$(x^n,{\hat{y}}^n)$ $\hat{y}$：Class1 = 1，Class2 = 0 $L(f)={\sum }_{n}C(f(x^n),{\hat{y}}^n)$	Training data:$(x^n,{\hat{y}}^n)$ ${\hat{y}}^n$：real value $L(f)=\frac{1}{2}{\sum }_n(f(x^n)-{\hat{y}}^n{)}^2$
Step 3：	$w_i=w_i-\eta {\sum }_n-(\hat{y}-f_{w,b}(x^n))x_i^n$	$w_i=w_i-\eta {\sum }_n-({\hat{y}}^n-f_{w,b}(x^n))x_i^n$

交叉熵：$C(f(x^n),{\hat{y}}^n)=-[{\hat{y}}^{n}ln{f}_{w,b}(x^n)+(1-\hat{y}n)ln(1-f_{w,b}(x^n))]$

(2) Discrimination和Generative(判别模型与生成模型)

	Discrimination Model	Generative Model
Function	$P(C_1	x) = \sigma(w.x+b)$
Target	$w$ , $b$	${\mu }^1$,${\mu }^2$,${\Sigma }^{-1}$

生成模型的好处

• 对于较少的训练数据，比较有效；
• 针对具有噪音的数据（数据标记有问题）有效；
• 可以从不同来源估计先验概率和类依赖概率。

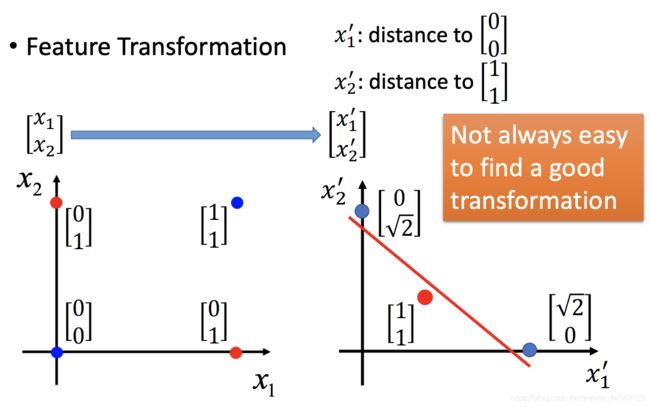
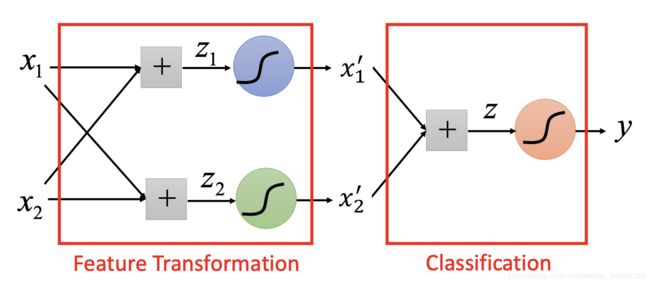
(3) Limitation of Logistic Regression

Logistic Regression模型具有限制，因为根据Logistic Regression模型找到的分类函数是一条直线，针对某些情况，会出现不适用：

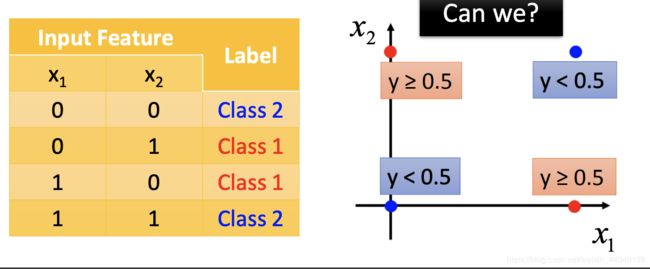
如图，你无法找到一条直线将Class1和Class2完全分开。

解决方法：

• 特征转化，转化成容易分类的特征：
  

• 级联逻辑回归模型：
  

二、学习打卡

(1) Logistic Regression损失函数

LR损失函数的作用就是评价函数的好坏，也就是Step 2：Goodness of a Function，这个作用。

1. 假设，训练数据如下：
   

假设存在$f_{w,b}(x)=P_{w,b}(C_1|x)$，表示选出$x$的条件下，$x$是属于$C_1$的概率。

2. 根据之前的学习，为了求到最优参数$w$和$b$，设计损失函数：
   $$L(w,b)=f_{w,b}(x^1)f_{w,b}(x^2)(1-f_{w,b}(x^3))\dots \text{\hspace{1em}(1.1)}$$
   最优的$w^{\ast }$和$b^{\ast }$就是使损失函数值最大的那对：
   $$w^{\ast },b^{\ast }=arg\underset{w,b}{\max }L(w,b)=arg\underset{w,b}{\min }-lnL(w,b)\text{\hspace{1em}(1.2)}$$

3. 于是，可得：
   $$-lnL(w,b)=-ln{f}_{w,b}(x^1)-ln{f}_{w,b}(x^2)-ln(1-f_{w,b}(x^3))...\text{\hspace{1em}(1.3)}$$

4. 转变数据对应方式：
   

图中有错误，${\hat{y}}^2=1$，以及${\hat{y}}^3=0$。因此，推导公式变成以下形式：

$$\begin{gathered} -ln{f}_{w,b}(x^1)=-[{\hat{y}}^{1}lnf(x^1)+(1-{\hat{y}}^1)ln(1-f(x^1))] \\ -ln{f}_{w,b}(x^2)=-[{\hat{y}}^{2}lnf(x^2)+(1-{\hat{y}}^2)ln(1-f(x^2))] \\ -ln(1-f_{w,b}(x^3))=-[{\hat{y}}^{3}lnf(x^3)+(1-\hat{y}3)ln(1-f(x^3))]\text{\hspace{1em}(1.4)} \end{gathered}$$

结果如图：

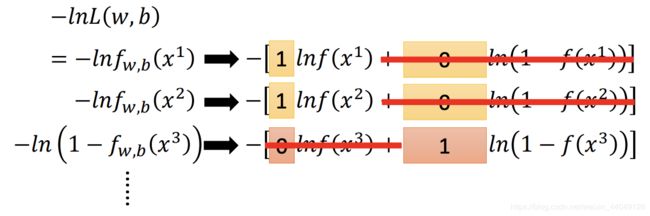
5. 对公式 (1.1)(1.3)(1.4)综合，得到下式：
$$\begin{gathered} L(w,b)=f_{w,b}(x^1)f_{w,b}(x^2)(1-f_{w,b}(x^3))\dots f_{w,b}(x^N) \\ -lnL(w,b)=-ln{f}_{w,b}(x^1)-ln{f}_{w,b}(x^2)-ln(1-f_{w,b}(x^3))... \\ -lnL(w,b)=\sum _n[{\hat{y}}^{n}ln{f}_{w,b}(x^n)+(1-{\hat{y}}^n)ln(1-f_{w,b}(x^n))]\text{\hspace{1em}(1.5)} \end{gathered}$$
6. 最后，展示如下图所示的形式：

其中cross entropy是交叉熵，表示两个分布p和q之间的接近程度。

(2) Logistic Regression梯度下降

LR梯度下降的目的就是在LR损失函数的基础上，找到最好的函数。

1. 根据推导结果公式1.5，损失函数对$w$进行偏微分：
   $$\frac{-lnL(w,b)}{\partial w_i}=\sum _n[{\hat{y}}^n\frac{ln{f}_{w,b}(x^n)}{\partial w_i}+(1-{\hat{y}}^n)\frac{ln(1-f_{w,b}(x^n))}{\partial w_i}]\text{\hspace{1em}(2.1)}$$

2. 根据上一节课程的结果，知道：函数$f_{w,b}(x)$是一个关于$z$的SIGMOD函数：
   $$\begin{gathered} f_{w,b}(x)=\sigma (z)=\frac{1}{1+e^{-z}} \\ z=w.x+b=\sum _i{w}_i{x}_i+b\text{\hspace{1em}(2.2)} \end{gathered}$$

3. 计算公式（2.1）的偏微分，首先计算左侧偏微分：
   $$\frac{\partial ln{f}_{w,b}(x)}{\partial w_i}=\frac{\partial ln{f}_{w,b}(x)}{\partial z}.\frac{\partial z}{\partial w_i}\text{\hspace{1em}(2.3)}$$
   结合公式（2.2）对公式（2.3）细分：
   $$\frac{\partial ln{f}_{w,b}(x)}{\partial z}=\frac{\partial ln\sigma (z)}{\partial z}=\frac{1}{\sigma (z)}.\frac{\partial \sigma (z)}{\partial z}=\frac{1}{\sigma (z)}.\sigma (z)(1-\sigma (z))=1-\sigma (z)\text{\hspace{1em}(2.4)}$$

$$\frac{\partial z}{\partial w_i}=x_i\text{\hspace{1em}(2.5)}$$

结合公式(2.4)和(2.5)，可得：
$$\frac{\partial ln{f}_{w,b}(x)}{\partial w_i}=(1-f_{w,b}(x^n))x_i^n\text{\hspace{1em}(2.6)}$$
同理，计算公式(2.1)右侧的偏微分：
$$\frac{\partial ln(1-f_{w,b}(x))}{\partial w_i}=\frac{\partial (1-ln{f}_{w,b}(x))}{\partial z}.\frac{\partial z}{\partial w_i}\text{\hspace{1em}(2.7)}$$
结合公式（2.2）对公式（2.7）细分：
$$\frac{\partial ln(1-f_{w,b}(x))}{\partial w_i}=\frac{1}{1-\sigma (z)}.\frac{\partial \sigma (z)}{\partial z}=\frac{1}{1-\sigma (z)}.\sigma (z)(1-\sigma (z))=\sigma (z)\text{\hspace{1em}(2.8)}$$

$$\frac{\partial z}{\partial w_i}=x_i\text{\hspace{1em}(2.9)}$$
结合公式(2.8)和(2.9)，可得：
$$\frac{\partial ln(1-f_{w,b}(x))}{\partial w_i}=f_{w,b}(x^n)x_i^n\text{\hspace{1em}(2.10)}$$

4. 将偏微分计算结果代入公式(2.1)中，可得：
   $$\begin{gathered} \frac{-lnL(w,b)}{\partial w_i}=\sum _n-[{\hat{y}}^n(1-f_{w,b}(x^n))x_i^n-(1-{\hat{y}}^n)f_{w,b}(x^n)x_i^n] \\ =\sum _n-(\hat{y}-f_{w,b}(x^n))x_i^n\text{\hspace{1em}(2.11)} \end{gathered}$$
   因此，梯度下降的迭代式：
   $$w_i=w_i-\eta \sum _n-(\hat{y}-f_{w,b}(x^n))x_i^n\text{\hspace{1em}(2.12)}$$
   从结果来看，当前输出$f_{w,b}(x^n)$与实际值$\hat{y}$的差距越大，梯度更新值越大。

(3) Softmax原理

在机器学习中，softmax函数广泛使用于多分类的场景中。他把一些输入映射为0-1之间的实数，并且归一化保证和为1，因此多分类的概率之和也刚好为1。因此，经过softmax处理后的数据，输出的是每个分类被取到的概率。下图是李老师在课件中展示的softmax计算原理：

假设有一系列不同类别的数，$z_i$表示第$i$个元素，一共有$j$个数。这个元素的softmax值就是：
$$S_i=\frac{e^{z_i}}{{\sum }_j{e}^{z_j}}$$

(4) softmax损失函数

首先，重新定义一个Softmax函数：
$$S_i=\frac{e^{V_i}}{{\sum }_i^C{e}_i^V}\text{\hspace{1em}(3.1)}$$
其中，$V_i$ 是经过模型函数之后输出的值。$i$表示第$i$类，总的类别个数为$C$。$S_i$ 表示的是当前元素的指数与所有元素指数和的比值。

根据上节可知，softmax的输出是：
$$S_i=\frac{e^{S_{y_i}}}{{\sum }_{j=1}^C{e}^{S_j}}\text{\hspace{1em}(3.2)}$$
$S_{y_i}$是正确类别对应的线性得分函数，$S_i$ 是正确类别对应的 Softmax输出。由于 $ln$ 运算符不会影响函数的单调性，我们对 $S_i$ 进行 $ln $操作：
$$ln{S}_i=ln\frac{e^{S_{y_i}}}{{\sum }_{j=1}^C{e}^{S_j}}\text{\hspace{1em}(3.3)}$$
我们希望 $S_i $越大越好，即正确类别对应的相对概率越大越好，在 $ln{S}_i$ 前面加个负号，表示损失函数：
$$L_i=-ln{S}_i=-ln\frac{e^{S_{y_i}}}{{\sum }_{j=1}^C{e}^{S_j}}\text{\hspace{1em}(3.4)}$$
进一步处理：
$$L_i=-ln\frac{e^{S_{y_i}}}{{\sum }_{j=1}^C{e}^{S_j}}=-(s_{y_i}-ln\sum _{j=1}^C{e}^{s_j})=-s_{y_i}+ln\sum _{j=1}^C{e}^{s_j}\text{\hspace{1em}(3.5)}$$
于是，损失函数简化成公式(3.5)。

(5) Softmax梯度下降

Softmax梯度下降是对权重参数进行求导：
$$\frac{\partial L_i}{\partial w_i}=\frac{-s_{y_i}+ln{\sum }_{j=1}^C{e}^{s_j}}{\partial w_i}=\frac{-s_{y_i}}{\partial w_i}+\frac{ln{\sum }_{j=1}^C{e}^{s_j}}{\partial w_i}\text{\hspace{1em}(4.1)}$$
其中，$s_{y_j}=w_i.x+b_i$，$s_j=w_j.x+b_j$
$$\begin{gathered} \frac{-s_{y_i}}{\partial w_i}=\frac{-(w_i.x+b_i)}{\partial w_i}=-x \\ \frac{ln{\sum }_{j=1}^C{e}^{s_j}}{\partial w_i}=\frac{ln{e}^{s_1}+ln{e}^{s_2}+...+ln{e}^{s_C}}{\partial w_i}=\frac{x}{w_1.x+b_1}+\frac{x}{w_2.x+b_2}+...+\frac{x}{w_C.x+b_C}\text{\hspace{1em}(4.2)} \end{gathered}$$
最终，得到:
$$\frac{\partial L_i}{\partial w_i}=-x+\sum _j^C\frac{x}{w_j+b_j}\text{\hspace{1em}(4.3)}$$
因此，梯度下降的迭代式:
$$w_i=w_i-\eta (-x+\sum _j^C\frac{x}{w_j+b_j})\text{\hspace{1em}(4.4)}$$