python机器学习 - 走进集成学习的世界(装袋法 - bagging,自适应增强 - adaptive boosting)
文章目录
- 集成学习,who are you?
- 集成(ensembles)
- 多数投票
- wrap up
- 集成学习,要你何用?
- 集成学习,怎么用?
- 装袋法 - Bagging(bootstrap aggregating)
- 自适应增强 - adaptive boost(AdaBoost)
- 增强(boosting)
- 工作原理
- 加权处理
source:python machine learning 3rd
集成学习是机器学习领域相当重要的一个概念,本篇文章中所关注的集成学习就是使用多个模型,采用同一训练集进行训练后,对样本运行多数投票的方式来确定分类,如果你不关注多数投票而是渴求更加高深莫测的算法,那么这篇基础性的文章将不值得你花费时间
如果完全掌握集成学习的是你的目标,阅读原著会带来更好的效果:)
集成学习,who are you?
我们对集成学习首先要有一个整体的把握和初步的了解,为此,以下几个概念需要重点掌握
集成(ensembles)
集成顾名思义,就是多个不同的模型所构成的集合,而如何获得集成则因具体的集成学习算法决定,这将在我们后文中提到。
总体而言,有两种思路可以帮助我们获得集成:
- 同一数据集,同一训练集,不同预测模型,比如使用逻辑回归,SVM,适应机等算法模型对同一组训练集进行训练后,这些不同的算法模型就组成了一组集成
- 同一数据集,不同训练集,同一预测模型, 最典型的就是随机森林,将训练集分成多个子集,模型算法相同,不同子集训练出来的各个模型组成一组集成
多数投票
多数投票是集成学习中最有效,最常用的决策机制,而且它同样可以运用到多类分类问题中:

- 绝对多数(majority):应用于二分类问题,样本分类结果为总投票中超过50%的分类
- 相对多数(plurality):应用于多类分类问题,样本分类结果为总投票中相对其它投票而言票数最多的分类
wrap up
拥有了集成和多数投票,集成学习算法对新数据进行预测就是顺水推舟的事情了,一图以弊之:
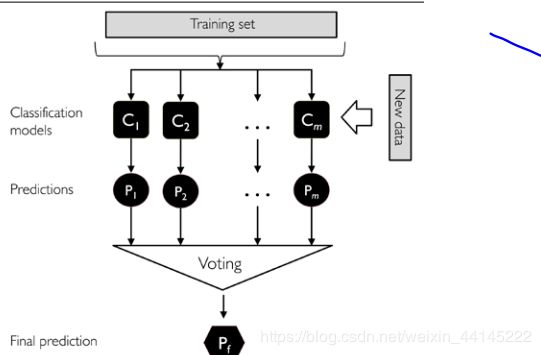
集成学习,要你何用?
大幅排版已经飘过,但谁能告诉我为什么要使用这玩意?
不妨假设一个集成中有11个模型,平均预测准确度为0.25,于是,将这个模型视为一个11重伯努利问题,开动数学脑筋,我们可以将预测错误的概率用如下方式表达:
P ( y ≥ k ) = ∑ k n ⟨ k n ⟩ ε k ( 1 − ε ) n − k = ε ensemble P(y \geq k)=\sum_{k}^{n}\left\langle_{k}^{n}\right\rangle \varepsilon^{k}(1-\varepsilon)^{n-k}=\varepsilon_{\text {ensemble }} P(y≥k)=k∑n⟨kn⟩εk(1−ε)n−k=εensemble
于是乎:
P ( y ≥ k ) = ∑ k = 6 11 C 11 k 0.2 5 k ( 1 − 0.25 ) 11 − k = 0.034 P(y \geq k)=\sum_{k=6}^{11}C_{11}^k 0.25^{k}(1-0.25)^{11-k}=0.034 P(y≥k)=k=6∑11C11k0.25k(1−0.25)11−k=0.034
其中k=6,p=0.25, P表示多数投票为错误分类的概率, ⟨ n k ⟩ \left\langle\begin{array}{l} n \\ k \end{array}\right\rangle ⟨nk⟩即为我们高中学过的 C n k C_{n}^k Cnk,很明显,得出的结果错误率为0.034明显小于单一模型的平均错误率,还有什么理由不适用集成学习呢?
当然,从严谨的角度来讲并不是所有情况下使用集成学习都能达到较好的效果,当集成中模型的平均错误率大与0.5时,使用集成学习会产生反作用
具体的情况图:
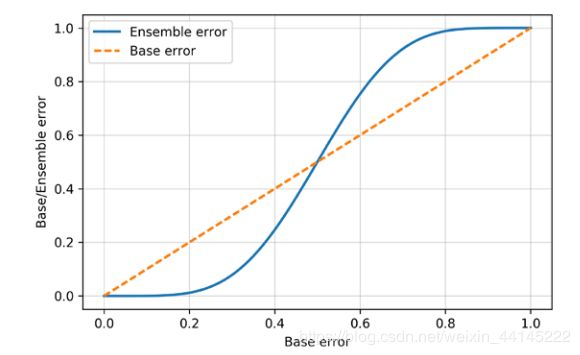
从图中我们可以直观地看出,集成中模型的平均错误率越小,使用集成学习的效果越显著
除了提高模型的准确度之外,集成学习还能帮助我们缓解高方差(过拟合)
集成学习,怎么用?
装袋法 - Bagging(bootstrap aggregating)
Bagging装袋法又名bootstrap aggregating自主聚合,bootstrap samples即随机有返回的子集,在这个抽象的名称背后,关于bagging是什么,你只需要直观地了解以下几点:
- bagging属于同一数据集,不同训练集,相同算法模型的集成学习方法
- bagging与常规集成学习多数投票的最大区别(唯一区别)就在于训练集的抽取是随机有放回的从原始训练数据集中抽取子集
- bagging一般用于决策树(decision tree)同时对所有算法通用;随机森林是一种特殊的装袋法,因为随机森林的训练集是由原始训练集随机选择特征维度产生的
关于装袋法随机抽取训练集这一过程,我们需要稍加注意:

训练每一个模型(C1,C2,C3.。。。)所使用的样本数和原始训练集是一样的(这在装袋法中不是必须的,但是样本量不多的时候建议遵守这个原则),只不过是由有放回的抽取样本获得的,其中每一次通过装袋法获得训练集依次称为一轮装袋,二轮装袋,三轮装袋等
装袋法的核心思想就体现在随机不放回地抽取训练样本方面,它的使用流程和warp up部分的图一摸一样
自适应增强 - adaptive boost(AdaBoost)
增强(boosting)
自适应增强是最好用,最常用的增强学习实现方法
增强学习适用于集成学习中的弱学习模型(weak learners),具体而言,就是指集成学习中那些简单的基础分类器,它们的表现只比随便乱猜(0.5)好一点。典型的弱学习模型有决策树桩
面对弱学习模型,增强学习关注于哪些难以区分的样本,然后让弱学习模型从错误分类中自我学习来提升集成学习的表现
增强(包括自适应增强)能够同时缓解高偏置和高方差,但是与bagging相比,自适应增强高方差(过拟合)的趋势更强
工作原理
关键四步骤(如果理解上还存在困难,可以先把正体部分看一遍,再结合看图和斜体部分):
- 从原始训练集中不放回地随机选择多个样本形成一个子集 d 1 d_1 d1,来训练一个弱学习模型 C 1 C_1 C1
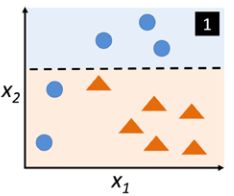
使用决策树桩进行第一次分类时的情形,选择出的子集为蓝色样本, 决策树桩切了一刀(决策边界),分类效果很不好 - 适用同样的方法获得第二个子集 d 2 d_2 d2,并且加上50%第一轮训练( C 1 C_1 C1)所预测出来的错误样本来训练另一个弱学习模型 C 2 C_2 C2
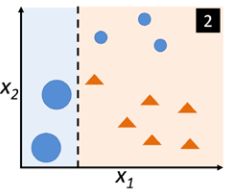
注意第一次训练后,已预测正确的样本减少权重,预测错误的样本增加权重。这样一来第二轮训练的弱学习模型就会重点在一轮错误预测模型旁边再切一刀,而不那么关注其它的样本 - 使用 C 1 , C 2 C_1, C_2 C1,C2来预测原始训练集中剩下的样本,将预测结果不同的样本组成第三组训练集 d 3 d_3 d3,使用其训练第三个弱学习模型 C 3 C_3 C3
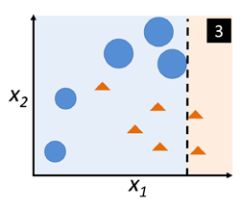
进入到第三次训练,将之前两次模型预测不同的数据都增大加权,使得决策树桩为了区分出所有的这些蓝点,即使错误预测结果很多也要沿x2再切一刀 - 使用 C 1 , C 2 , C 3 C_1, C_2,C_3 C1,C2,C3进行多数投票
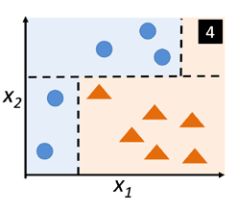
被切了三刀之后,进行多数投票。很明显,蓝色样本得了两票,橙色样本只得了一票,其决策边界正好为三刀分切领域的求交
实践中的自适应增强效果当然不会这么完美,但也是很棒棒的了
加权处理
尽管模型看上去很好的样子,但是疑团乌云已经出现,那就是加权。调一调权重怎么就能有这么好的效果了呢?
背后的数学原理也许深奥晦涩,但是呈现出权重操作的自适应增强过程也许能够帮助理解:
- 设置和为1,值相同的权重矢量 w w w
- 在m轮增强中,对j(j=1,2,3 … m):
- 训练一个弱学习模型: C j = train ( X , y , w ) C_{j}=\operatorname{train}(X, y, w) Cj=train(X,y,w)
- 预测结果: y ^ = predict ( C j , X ) \widehat{y}=\operatorname{predict}\left(C_{j}, X\right) y =predict(Cj,X)
- 计算加权错误率: ε = w ⋅ ( y ^ ≠ y ) \varepsilon=\boldsymbol{w} \cdot(\hat{\boldsymbol{y}} \neq \boldsymbol{y}) ε=w⋅(y^=y)
- 计算加权系数: α j = 0.5 log 1 − ε ε \alpha_{j}=0.5 \log \frac{1-\varepsilon}{\varepsilon} αj=0.5logε1−ε
- 使用系数更新加权: w : = w × exp ( − α j × y ^ × y ) \boldsymbol{w}:=\boldsymbol{w} \times \exp \left(-\alpha_{j} \times \widehat{\boldsymbol{y}} \times \boldsymbol{y}\right) w:=w×exp(−αj×y ×y)
- 均值化加权重新使其和为1: w : = w / ∑ i w i \boldsymbol{w}:=\boldsymbol{w} / \sum_{i} w_{i} w:=w/∑iwi
- 当第二步每轮处理都完成后,获得最总的预测结果: y ^ = ( ∑ j = 1 m ( α j × predict ( c j , X ) ) > 0 ) \hat{y}=\left(\sum_{j=1}^{m}\left(\alpha_{j} \times \operatorname{predict}\left(c_{j}, X\right)\right)>0\right) y^=(∑j=1m(αj×predict(cj,X))>0)
这其中涉及到了不少特殊公式的使用,很遗憾,讨论每个公式的原理意义已经在我的能力范围之外了。。。
希望这篇文章能够助益打开集成学习的大门,欢迎各位的建议,指正和补充