9. 小波变换与图像处理（上）

9.1 小波变换的背景

1）尽管傅立叶变换自上世纪50年代以来一直是变换域图像处理的基石，但90年代出现的一种新的变换（小波变换）成为一种新的流行信号处理工具。
2）与傅立叶变换(其基础函数是正弦曲线)不同，小波变换基于一些称作小波的小型波，它具有变化的频率和有限的持续时间。
3）若把图像看作是一个乐谱，小波变换不仅可揭示演奏的音符(或频率)，而且能揭示何时演奏；而傅里叶变换只能提供音符或频率信息。
4）小波变换常与多分辨理论联系在一起。多分辨率理论融合和统一了多个领域的技术，包括信号处理的子带编码、数字语音识别的正交镜像滤波和金字塔形图像处理。

9.2 图像金字塔

如下图：

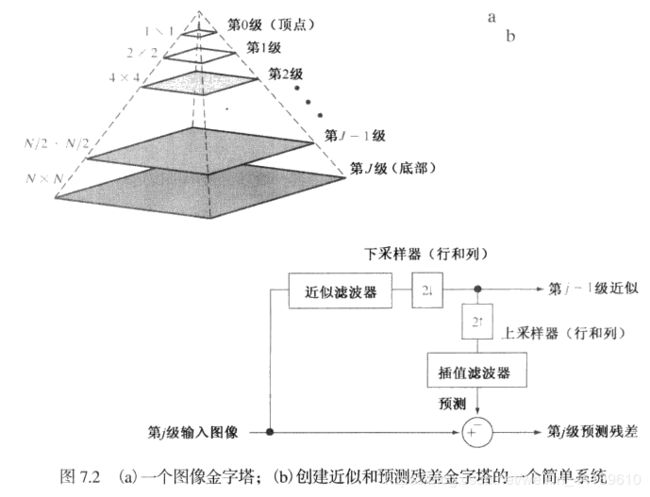
高斯金字塔示例：

一幅图像可以有多个分辨率来表示，这样做有利于在不同分辨率下对图像进行处理。对一张图片进行2倍下采样就可以得到低分辨率的图像表示。

9.3 子带编码

将一个信号分为两部分分别进行编解码后得到与输入信号相同的合成信号就叫子带编码，分成的两个部分就叫两个子带。

9.3.1 Z变换

1）Z变换的公式如下：

Z变换的性质：

其中 z 是一个复变量。

2）信号下采样的Z变换：

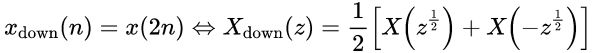
3）信号上采样的Z变换（用0填充）：

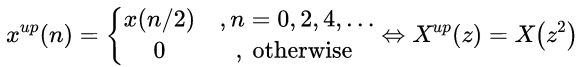
4）因此，一个信号经下采样与上采样后对应信号的Z变换为：

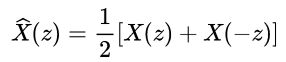
其中：

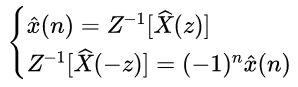
5）一个双子带编码和解码系统表示为：

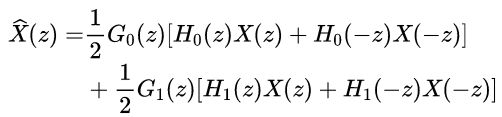
其中滤波器 的输出由下述变换对定义：

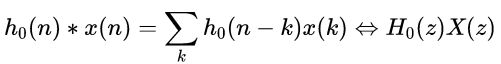
整理上式，得：

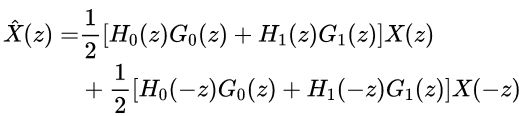
为了对输入进行无失真重建，我们可施加如下条件：

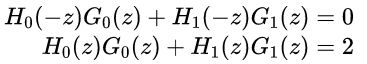
假定 是非奇异矩阵，可得：

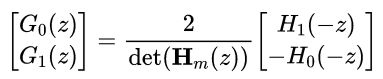
其中：

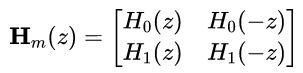
9.3.2 完美重建滤波器组(PCFB)的特性

1）上式告诉我们 是 的函数， 是 的函数。因此分析与合成滤波器是交叉调制的。
2） 双正交性

9.3.3 用于图像的二维子带滤波器

1）一维滤波器也可用于图像处理的二维可分离滤波器 。

图中滤波后的输出结果分别称为图像的近似值子带、垂直细节子带、水平细节子带和对角线细节子带。
一个或者多个这样的子带可被进一步分为4个更小的子带，以此类推。

2）完美重建滤波器的例子1： Daubechies正交滤波器：

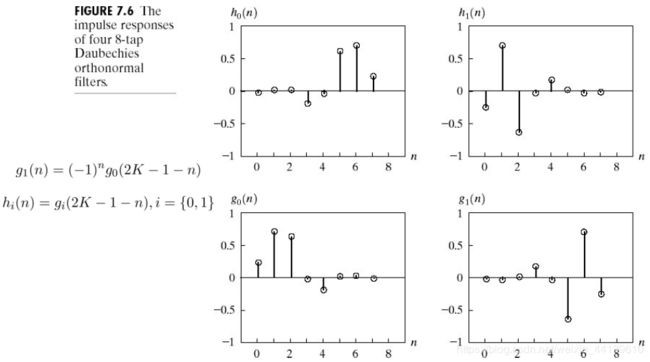
3）完美重建滤波器的例子2： 花瓶图像的四子带分解

9.4 哈尔变换

1）哈尔变换(Haar Transform)的基函数是众所周知的最古老也最简单的正交小波。
2）哈尔变换本身具有对称性和可分离性，可以用下述矩阵形式表达：

其中 F 是一个 N × N 图像矩阵， H 是 N × N 的变换矩阵， T是换的结果矩阵。
3）变换矩阵 H 包含哈尔基函数 ，它们定义在连续闭区间z属于[0, 1]上，其中K = 0,1,2 … N-1。
4）可根据如下式子生成H：

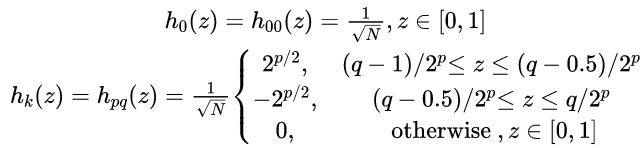
当 N =8时，对应的值为：

9.5 多分辨率分析（ Multi-resolution analysis ,MRA ）

1）在多分辨率展开(MRA)中，尺度函数被用于建立某一函数或图像的一系列近似值，而被称为小波的函数用于对相邻近似值之间的差异进行编码。
2）信号或函数 常可分解为一系列展开函数的线性组合，即：

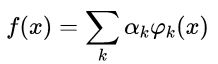
3）如果这种展开是唯一的，也就是说对任何指定的 ，只有一个系数序列与之相对应，则 称为基函数，展开序列 称为可表示的函数类的基。
4）可被表示的函数组成了一个函数空间，称为展开集合的闭合跨度，表示为：

对于任意函数空间 V 及其相应的展开函数集合 ，都存在一个对偶函数集{ }，通过计算其和的积分可得到系数 ,即：

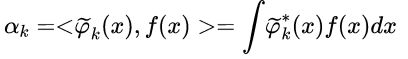
如果展开函数构成了 V 的一个正交基，即：

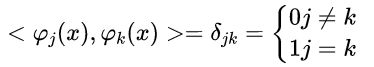
则基与它的对偶相等，因此：

9.6 尺度函数和小波函数

9.6.1 尺度函数

1）现在考虑由平方可积函数通过整数平移和二进制尺度缩放构成的函数组成的展开函数集合，即：

k决定了在x轴上的位置，j决定了的宽度，即沿x轴的宽或者窄的程度，而 控制其高度或者幅度。被称为尺度函数。通过选择适当的fai(x)，可以张成跨度L2®，即所有可测量的平方可积函数的集合 。
当j = j0时，是原来的一个子集：

2）Vj子空间的展开函数可以被表述为Vj+1子空间的展开函数的加权和：

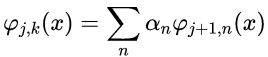
将an变成hfai(n):

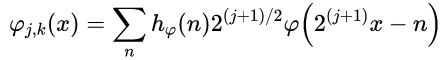
可得到更简单的无下标表达式：

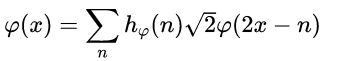
该式中hfai(n)称为尺度函数系数， 为尺度向量。该等式被称为精细化方程、MRA方程或者扩张方程。它表示任意子空间的展开函数都可以从它们自身的双分辨率副本中得到，即从相邻较高分辨率空间中得到。

3）尺度函数有如下的几个基本要求：
（1）尺度函数对它的整数平移对应的函数是正交的。
（a）哈尔函数被称为是紧支撑的，意味着除了称为支撑域有限区间外，函数值都为0。
（b）必须注意，当尺度函数的支撑域大于1时，整数平移函数间的正交性将变得更加难于被满足。
（2）低尺度尺度函数张成的子空间包含于高尺度尺度函数张成的子空间内。

（3）唯一包含在所有 中的函数是 ：

（4）任何函数都可以以任意精度表示。

4）哈尔尺度函数：

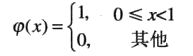
9.6.2 小波函数

1）给定了尺度函数，能够定义对应的小波函数 。利用它的整数平移及其二进制尺度缩放所构造的函数集，可以张成相邻两尺度子空间的差异，即Vj与Vj+1。

2）定义小波函数集合：

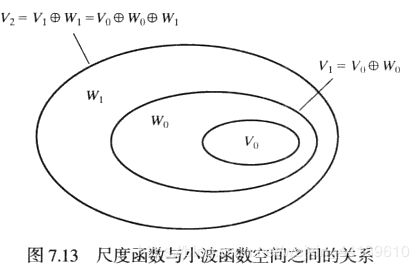
尺度和小波函数子空间的关系可由下式描述：

Vj+1中Vj的正交补集是Wj，且Wj中的所有成员对于Vj中的所有成员都正交，即：

任意j，k，l属于Z空间。
现在可将所有可测度的平方可积函数空间表示如下：

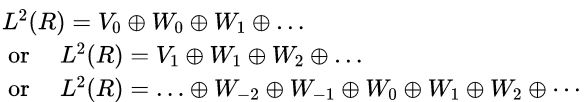
3）另外，我们有一般性的结果：

其中 为任意的起始尺度。
4）由于小波空间存在于由相邻较高分辨率尺度函数张成的空间中，所以任何小波函数可以表示成平移的双倍分辨率尺度函数的加权和：

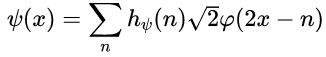
其中hfai(n)称为小波函数系数，hfai称为小波向量。
5）利用小波函数与尺度函数构成正交补空间，以及整数平移小波函数彼此正交的条件，可以证明尺度向量与小波向量之间具有如下关系：

6）哈尔小波函数：