剑指offer:java版
作者:CyC2018
链接:https
文章目录
- 一.基础
- 3.数组中的重复的数字
- 4. 二维数组中的查找
- 5. 替换空格
- 6. 从尾到头打印链表
- 7. 重建二叉树
- 8. 二叉树的下一个结点
- 9. 用两个栈实现队列
- 10.1 斐波那契数列
- 11.旋转数组的最小数字
- 12.矩阵中的路径
- 13.机器人的运动范围
- 14.剪绳子
- 15.二进制中1的个数
- 15.引申:
- 总结一
- 高质量代码
- 16. 数值的整数次方
- 17. 打印从 1 到最大的 n 位数
- 18.1 在 O(1) 时间内删除链表节点
- 18.2 删除链表中重复的结点
- 19. 正则表达式匹配
- 20. 表示数值的字符串
- 21. 调整数组顺序使奇数位于偶数前面
- 22.链表中倒数第k个节点
- 考试中遇到的题
- 1.最长上升子序列
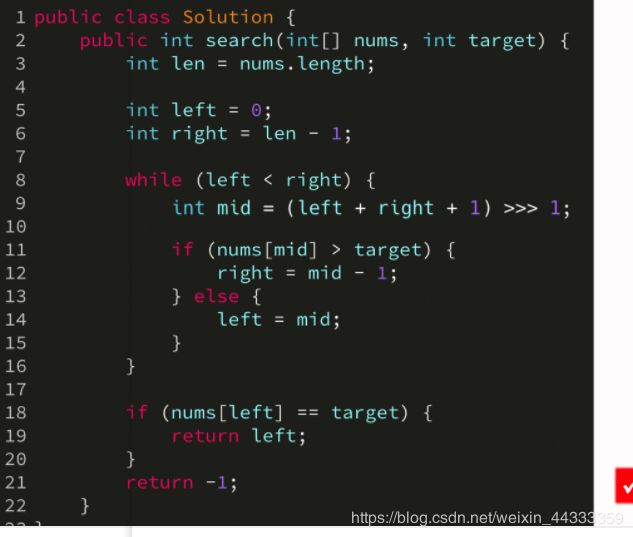
- 2.二分查找的模板
- 二分查找基本的代码
- x的平方根
- 寻找旋转排序数组中的最小值(不存在重复元素)
- 寻找旋转排序数组中的最小值||(存在重复元素)
- 寻找重复数
- 山脉数组中查找目标值
- 找到 K 个最接近的元素
- 3.判断s1字符串的全排列是否包含在s2中 Permutation in String
- 最长回文串
- 求两个数的二进制有多少位不同
- 由整数对(父节点和子节点的关系)组成的二叉树的高度问题
一.基础
3.数组中的重复的数字
题目描述
在一个长度为 n 的数组里的所有数字都在 0 到 n-1 的范围内。数组中某些数字是重复的,但不知道有几个数字是重复的,也不知道每个数字重复几次。请找出数组中任意一个重复的数字。
要求时间复杂度 O(N),空间复杂度 O(1)。因此不能使用排序的方法,也不能使用额外的标记数组。

解题思路:
1.数组排序
时间O(nlogn)
空间O(1)
2.哈希表/数组
时间O(1)
空间O(n)
3.新思路:
修改原数组找到所有的重复数字
对于这种数组元素在 [0, n-1] 范围内的问题,可以将值为 i 的元素调整到第 i 个位置上进行求解。
以 (2, 3, 1, 0, 2, 5) 为例,遍历到位置 4 时,该位置上的数为 2,但是第 2 个位置上已经有一个 2 的值了,因此可以知道 2 重复:
时间O(n)
空间O(1)
若不要求空间复杂度为O(1),则可以加一个辅助数组,将每个数m复制到下标为m的辅助数组中,这样比较容易发现重复数。
public boolean duplicate(int[] nums, int length, int[] duplication) {
if (nums == null || length <= 0)
return false;
for (int i = 0; i < length; i++) {
while (nums[i] != i) {
if (nums[i] == nums[nums[i]]) {
duplication[0] = nums[i];
return true;
}
swap(nums, i, nums[i]);
}
}
return false;
}
private void swap(int[] nums, int i, int j) {
int t = nums[i];
nums[i] = nums[j];
nums[j] = t;
}
4.新思路:
不修改数组的情况下找到任意重复数字
按照二分法的思想去完成。
时间O(logn)
空间O(1)
public int duplicate(int numbers[],int length) {
if(numbers==null||length<=0)return -1;
int start=1;
end=length-1;
while(start<=end){
mid=(end-start)>>1+start;
int count=countRange(numbers,start,mid);
if(start==end){
if(count>1)
return start;
else
break;
}
if(count>(mid-start+1))
end=mid;
else
start=mid+1;
}
return -1;
}
int countRange(int[] numbers,int start,int mid){
if(numbers==null)return 0;
int count=0;
for(int i=0;i=start&&numbers[i]<=mid)
count++;
}
return count;
}
4. 二维数组中的查找
题目描述
给定一个二维数组,其每一行从左到右递增排序,从上到下也是递增排序。给定一个数,判断这个数是否在该二维数组中。

时间:O(M+N) M行N列
空间:O(1)
public boolean Find(int target, int[][] matrix) {
if (matrix == null || matrix.length == 0 || matrix[0].length == 0)
return false;
int rows = matrix.length, cols = matrix[0].length;
int r = 0, c = cols - 1; // 从右上角开始
while (r <= rows - 1 && c >= 0) {
if (target == matrix[r][c])
return true;
else if (target > matrix[r][c])
r++;
else
c--;
}
return false;
}
5. 替换空格
题目描述
将一个字符串中的空格替换成 “%20”。

思路在书上《剑指offer》
时间O(n)
空间O(1)
剑指
针对字符串操作
作者:CyC2018
链接:https://www.nowcoder.com/discuss/198840
来源:牛客网
几个字符串常用的方法:charAt(i)字符串下标为i的字符
setCharAt(i,b)将字符串i下标的字符转换成b
public String replaceSpace(StringBuffer str) {
int P1 = str.length() - 1;
for (int i = 0; i <= P1; i++)
if (str.charAt(i) == ' ')
str.append(" ");
int P2 = str.length() - 1;
while (P1 >= 0 && P2 > P1) {
char c = str.charAt(P1--);
if (c == ' ') {
str.setCharAt(P2--, '0');
str.setCharAt(P2--, '2');
str.setCharAt(P2--, '%');
} else {
str.setCharAt(P2--, c);
}
}
return str.toString();
}
左宗云P266
针对字符数组操作
public void replace(char[] chas){
if(chas==null||chas.length==0)
return;
int num=0;
int len=0;
for(len=0;len=0;i--){
if(chas[i]!=" "){
chas[j]=chas[i];
j--;
}else{
chas[j--]="0";
chas[j--]="2";
chas[j--]="%";
}
}
}
左宗云的补充问题
给定一个字符数组,只含"*“和数字字符,现在想把所有的”*"挪到数组的左边,把所有的数字字符挪到数组的右边。
思想:从右向左遍历,遇到数字字符直接赋值,遇到*字符不复制。把数字字符复制完后,再把左半区全部设置成*。
代码:
public void modify(char[] chas)[
if(chas==null||chas.length==0){
return;
}
int j=chas.length-1;
for(int i=chas.length-1:i>=0;i--){
if(chas[i]!='*')
chas[j--]=chas[i];
}
for(;j>=0;j--){
chas[j]='*';
}
}
总结
合并两个数组/字符串,一般考虑从后向前遍历这个节省时间,减少移动次数,提高效率。
6. 从尾到头打印链表
题目描述:
从尾到头反过来打印出每个结点的值。
关注点:要问面试官是否改变原来结构。
改变原来结构
1.逆序链表
链表的插入分为头插法和尾插法:头插法是,每次插入节点在头部,就是将链表逆序。尾插法就是在链表尾部插入新节点,按正常顺序插入。
使用头插法:
使用头插法可以得到一个逆序的链表。
头结点和第一个节点的区别:
头结点是在头插法中使用的一个额外节点,这个节点不存储值;
第一个节点就是链表的第一个真正存储值的节点。
不改变原来结构
2.使用辅助空间栈
public ArrayList printListFromTailToHead(ListNode listNode) {
Stack stack = new Stack<>();
while (listNode != null) {
stack.add(listNode.val);
listNode = listNode.next;
}
ArrayList ret = new ArrayList<>();
while (!stack.isEmpty())
ret.add(stack.pop());
return ret;
}
3.递归(也是利用栈)
链表常用方法:
res.addAll(list):将list中的节点都加入链表中
res.add(1):将一个节点加入链表
这时候出现一个问题,当链表非常长的时候,就会导致函数调用的层级很深,从而有可能导致函数调用栈溢出。
public ArrayList printListFromTailToHead(ListNode listNode) {
ArrayList res=new ArrayList();
if(listNode!=null){
res.addAll(printListFromTailToHead(listNode.next));
res.add(listNode.val);
}
return res;
}
7. 重建二叉树
题目描述
1.根据二叉树的前序遍历和中序遍历的结果,重建出该二叉树。假设输入的前序遍历和中序遍历的结果中都不含重复的数字。
我加的
2.中序和后序建树
后序的最后一个和中序的中间为树的根节点。
相似于前序和中序
????3.前序和后序建树
代码:
1.前序和中序
根据中序数组来找到根节点,求出左子树长度
解析
class Solution {
public TreeNode buildTree(int[] preorder, int[] inorder) {
if(preorder == null || inorder == null)
return null;
return build(preorder, inorder, 0, 0, inorder.length - 1);
}
private TreeNode build(int[] preorder, int[] inorder, int preStart, int inStart, int inEnd) {
if(preStart > preorder.length - 1 || inStart > inEnd)
return null;
TreeNode root = new TreeNode(preorder[preStart]);
int index = 0;
for(int i = inStart; i <= inEnd; i ++) {
if(inorder[i] == root.val) {
index = i;
break;
}
}
root.left = build(preorder, inorder, preStart + 1, inStart, index - 1);
root.right = build(preorder, inorder, preStart + index - inStart + 1, index + 1, inEnd);
return root;
}
}
8. 二叉树的下一个结点
题目描述
给定一个二叉树和其中的一个结点,请找出中序遍历顺序的下一个结点并且返回。注意,树中的结点不仅包含左右子结点,同时包含指向父结点的指针。
节点的结构:
public class TreeLinkNode {
int val;
TreeLinkNode left = null;
TreeLinkNode right = null;
TreeLinkNode next = null;
TreeLinkNode(int val) {
this.val = val;
}
}
主要思想:
① 如果一个节点的右子树不为空,那么该节点的下一个节点是右子树的最左节点;
② 否则,向上找第一个左链接指向的树包含该节点的祖先节点。(这一分支中判断此节点是父节点的左节点,那么下一节点就是父节点,否则向上一直找就好了)
代码:
作者:CyC2018
链接:https://www.nowcoder.com/discuss/198840
来源:牛客网
public TreeLinkNode GetNext(TreeLinkNode pNode) {
if (pNode.right != null) {
TreeLinkNode node = pNode.right;
while (node.left != null)
node = node.left;
return node;
} else {
while (pNode.next != null) {
TreeLinkNode parent = pNode.next;
if (parent.left == pNode)
return parent;
pNode = pNode.next;
}
}
return null;
}
9. 用两个栈实现队列
用两个栈来实现一个队列,完成队列的 Push 和 Pop 操作。
主要思想:
in 栈用来处理入栈(push)操作,out 栈用来处理出栈(pop)操作。一个元素进入 in 栈之后,出栈的顺序被反转。当元素要出栈时,需要先进入 out 栈,此时元素出栈顺序再一次被反转,因此出栈顺序就和最开始入栈顺序是相同的,先进入的元素先退出,这就是队列的顺序。
代码:
作者:CyC2018
链接:https://www.nowcoder.com/discuss/198840
来源:牛客网
Stack in = new Stack();
Stack out = new Stack();
public void push(int node) {
in.push(node);
}
public int pop() throws Exception {
if (out.isEmpty())
while (!in.isEmpty())
out.push(in.pop());
if (out.isEmpty())
throw new Exception("queue is empty");
return out.pop();
}
引申:用两个队列来实现栈。
两个队列模拟栈的压入数据和弹出数据。
10.1 斐波那契数列
题目描述
求斐波那契数列的第 n 项,n <= 39。
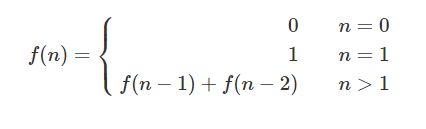
在左宗云的书上有多种时间复杂度的算法。参考这本书。还会加上一些扩展的题会和动态规划有关系
1.递归。
public int f1(int n){
if(n<1)
return 0;
if(n==1)
return 1;
return f1(n-1)+f2(n-2);
}
时间复杂度是O(2*(N))
缺点:效率不高、会有重复的计算、当n太大时,会产生调用栈溢出。
2.将每个指在map中存储 ,利用数组将子问题缓存起来,避免重复计算。
作者:CyC2018
链接:https://www.nowcoder.com/discuss/198840
来源:牛客网
public int Fibonacci(int n) {
if (n <= 1)
return n;
int[] fib = new int[n + 1];
fib[1] = 1;
for (int i = 2; i <= n; i++)
fib[i] = fib[i - 1] + fib[i - 2];
return fib[n];
}
再辅助空间有点大,所以改进,考虑第i项和第i-1和i-2项有关,因此只需存储前两项的值就可。
作者:CyC2018
链接:https://www.nowcoder.com/discuss/198840
来源:牛客网
public int Fibonacci(int n) {
if (n <= 1)
return n;
int pre2 = 0, pre1 = 1;
int fib = 0;
for (int i = 2; i <= n; i++) {
fib = pre2 + pre1;
pre2 = pre1;
pre1 = fib;
}
return fib;
}
时间复杂度O(N)
3.矩阵方法:将斐波那契数列转换成矩阵乘法。
(F(n),F(n-1))=(F(n-1),F(n-2))* |1 1 |
|1 0 |
11.旋转数组的最小数字
题目描述
把一个数组最开始的若干个元素搬到数组的末尾,我们称之为数组的旋转。输入一个非递减排序的数组的一个旋转,输出旋转数组的最小元素。
解题思路
将旋转数组对半分可以得到一个包含最小元素的新旋转数组,以及一个非递减排序的数组。新的旋转数组的数组元素是原数组的一半,从而将问题规模减少了一半,这种折半性质的算法的时间复杂度为 O(logN)(为了方便,这里将 log2N 写为 logN)。
此时问题的关键在于确定对半分得到的两个数组哪一个是旋转数组,哪一个是非递减数组。我们很容易知道非递减数组的第一个元素一定小于等于最后一个元素。
通过修改二分查找算法进行求解(l 代表 low,m 代表 mid,h 代表 high):
当 nums[m] <= nums[h] 时,表示 [m, h] 区间内的数组是非递减数组,[l, m] 区间内的数组是旋转数组,此时令 h = m;
否则 [m + 1, h] 区间内的数组是旋转数组,令 l = m + 1。
思想:对于二分查找的引申
public int minNumberInRotateArray(int[] nums) {
if (nums.length == 0)
return 0;
int l = 0, h = nums.length - 1;l指向前面的顺序数组第一个数字,h指向后面顺序数组的最后数字。两个指针分别向中间移动。
while (l < h) {
int m = l + (h - l) / 2;//查找中间点
if (nums[m] <= nums[h])
h = m;
else
l = m + 1;
}
return nums[l];
}
如果数组元素允许重复,会出现一个特殊的情况:nums[l] == nums[m] == nums[h],此时无法确定解在哪个区间,需要切换到顺序查找。例如对于数组 {1,1,1,0,1},l、m 和 h 指向的数都为 1,此时无法知道最小数字 0 在哪个区间。
public int minNumberInRotateArray(int[] nums) {
if (nums.length == 0)
return 0;
int l = 0, h = nums.length - 1;
while (l < h) {
int m = l + (h - l) / 2;
if (nums[l] == nums[m] && nums[m] == nums[h])
return minNumber(nums, l, h);//开头结尾数字都相等,使用顺序查找
else if (nums[m] <= nums[h])
h = m;
else
l = m + 1;
}
return nums[l];
}
private int minNumber(int[] nums, int l, int h) {//顺序查找
for (int i = l; i < h; i++)
if (nums[i] > nums[i + 1])
return nums[i + 1];
return nums[l];
}
12.矩阵中的路径
题目描述
判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一个格子开始,每一步可以在矩阵中向上下左右移动一个格子。如果一条路径经过了矩阵中的某一个格子,则该路径不能再进入该格子。
解题思路
使用回溯法(backtracking)进行求解,它是一种暴力搜索方法,通过搜索所有可能的结果来求解问题。回溯法在一次搜索结束时需要进行回溯(回退),将这一次搜索过程中设置的状态进行清除,从而开始一次新的搜索过程。例如下图示例中,从 f 开始,下一步有 4 种搜索可能,如果先搜索 b,需要将 b 标记为已经使用,防止重复使用。在这一次搜索结束之后,需要将 b 的已经使用状态清除,并搜索 c。
本题的输入是数组而不是矩阵(二维数组),因此需要先将数组转换成矩阵。
代码分析:
几个矩阵:
private final static int[][] next = {{0, -1}, {0, 1}, {-1, 0}, {1, 0}};//向各自的上下左右移动
boolean[][] marked = new boolean[rows][cols];//布尔辅助矩阵,记录当前各自是否遍历过,初始值默认为false。
char[][] matrix = buildMatrix(array);//辅助矩阵,就是arry的copy数组
char[] str:是给的已知的路径数组
private final static int[][] next = {{0, -1}, {0, 1}, {-1, 0}, {1, 0}};//向各自的上下左右移动
private int rows;
private int cols;
//char[] str是给的已知的路径数组
public boolean hasPath(char[] array, int rows, int cols, char[] str) {//判断是否存在路径方法
if (rows == 0 || cols == 0) return false;
this.rows = rows;
this.cols = cols;
boolean[][] marked = new boolean[rows][cols];//布尔辅助矩阵
char[][] matrix = buildMatrix(array);//辅助矩阵
for (int i = 0; i < rows; i++)
for (int j = 0; j < cols; j++)
if (backtracking(matrix, str, marked, 0, i, j))//对辅助矩阵的每个各自进行回溯
return true;
return false;
}
private boolean backtracking(char[][] matrix, char[] str,
boolean[][] marked, int pathLen, int r, int c) {//回溯法的核心
if (pathLen == str.length) return true;
if (r < 0 || r >= rows || c < 0 || c >= cols
|| matrix[r][c] != str[pathLen] || marked[r][c]) {// marked[r][c]防止遍历当前各自的上下左右会有一次碰到回溯的前面的数字,即之前遍历过
return false;
}
marked[r][c] = true;
for (int[] n : next)
if (backtracking(matrix, str, marked, pathLen + 1, r + n[0], c + n[1]))
return true;
marked[r][c] = false;//当前各自的上下左右的各自否不满足条件,所以当前的各自的辅助矩阵设为false
return false;
}
private char[][] buildMatrix(char[] array) {//初始化辅助矩阵
char[][] matrix = new char[rows][cols];
for (int r = 0, idx = 0; r < rows; r++)
for (int c = 0; c < cols; c++)
matrix[r][c] = array[idx++];
return matrix;
}
13.机器人的运动范围
题目描述
地上有一个 m 行和 n 列的方格。一个机器人从坐标 (0, 0) 的格子开始移动,每一次只能向左右上下四个方向移动一格,但是不能进入行坐标和列坐标的数位之和大于 k 的格子。
例如,当 k 为 18 时,机器人能够进入方格 (35,37),因为 3+5+3+7=18。但是,它不能进入方格 (35,38),因为 3+5+3+8=19。请问该机器人能够达到多少个格子?
解题思路
回溯法
使用深度优先搜索(Depth First Search,DFS)方法进行求解。回溯是深度优先搜索的一种特例,它在一次搜索过程中需要设置一些本次搜索过程的局部状态,并在本次搜索结束之后清除状态。而普通的深度优先搜索并不需要使用这些局部状态,虽然还是有可能设置一些全局状态。
private static final int[][] next = {{0, -1}, {0, 1}, {-1, 0}, {1, 0}};//上下左右移动
private int cnt = 0;
private int rows;
private int cols;
private int threshold;
private int[][] digitSum;
public int movingCount(int threshold, int rows, int cols) {
this.rows = rows;
this.cols = cols;
this.threshold = threshold;
initDigitSum();//初始化各种辅助数组
boolean[][] marked = new boolean[rows][cols];//是否被遍历过的辅助数组
dfs(marked, 0, 0);//深度遍历
return cnt;
}
private void dfs(boolean[][] marked, int r, int c) {
if (r < 0 || r >= rows || c < 0 || c >= cols || marked[r][c])//过界或者已经遍历过这个各自,则返回
return;
marked[r][c] = true;//标记当前各自遍历过
if (this.digitSum[r][c] > this.threshold)//大于k就返回
return;
cnt++;//满足条件数量加一
for (int[] n : next)//对当前各自的上下左右进行深度遍历
dfs(marked, r + n[0], c + n[1]);
}
private void initDigitSum() {//数位相加,每个行列的数字的每一位相加
//辅助矩阵使用的压缩矩阵,即取行列长度最大的作为一维矩阵长度,每个元素求出对应数字的位数和
int[] digitSumOne = new int[Math.max(rows, cols)];//行列的最长的长度为辅助数组的长度
for (int i = 0; i < digitSumOne.length; i++) {
int n = i;
while (n > 0) {
digitSumOne[i] += n % 10;
n /= 10;
}
}
this.digitSum = new int[rows][cols];//二维数据中的每个格子都我求出对应行列的位数和。
for (int i = 0; i < this.rows; i++)
for (int j = 0; j < this.cols; j++)
this.digitSum[i][j] = digitSumOne[i] + digitSumOne[j];//算出二维矩阵的格子行列的位数和,即用辅助矩阵 int[] digitSumOne对应的数字的和。
}
14.剪绳子
题目描述
把一根绳子剪成多段,并且使得每段的长度乘积最大。
n = 2
return 1 (2 = 1 + 1)
n = 10
return 36 (10 = 3 + 3 + 4)
1.动态规划:
从上到下分析问题,从下到上解决问题。
public int integerBreak(int n) {
int[] dp = new int[n + 1];
dp[1] = 1;
for (int i = 2; i <= n; i++)
for (int j = 1; j < i; j++)
dp[i] = Math.max(dp[i], Math.max(j * (i - j), dp[j] * (i - j)));
return dp[n];
}
2.贪婪算法
尽可能多剪长度为 3 的绳子,并且不允许有长度为 1 的绳子出现。如果出现了,就从已经切好长度为 3 的绳子中拿出一段与长度为 1 的绳子重新组合,把它们切成两段长度为 2 的绳子。
证明:当 n >= 5 时,3(n - 3) - n = 2n - 9 > 0,且 2(n - 2) - n = n - 4 > 0。因此在 n >= 5 的情况下,将绳子剪成一段为 2 或者 3,得到的乘积会更大。又因为 3(n - 3) - 2(n - 2) = n - 5 >= 0,所以剪成一段长度为 3 比长度为 2 得到的乘积更大。
public int integerBreak(int n) {
if (n < 2)
return 0;
if (n == 2)
return 1;
if (n == 3)
return 2;
int timesOf3 = n / 3;//竟可能的剪多的3
的绳子
if (n - timesOf3 * 3 == 1)//最后剩4的长度就不剪3了,因为2*2>1*3
timesOf3--;
int timesOf2 = (n - timesOf3 * 3) / 2;//剩4的时候剪2
return (int) (Math.pow(3, timesOf3)) * (int) (Math.pow(2, timesOf2));//pow(x,y)是x的y次幂
}
15.二进制中1的个数
题目描述
输入一个整数,输出该数二进制表示中 1 的个数。
题目思想:
1.整数减1,和本身与运算直到整数n为0为止,循环次数为1个数。
时间复杂度:O(M),其中 M 表示 1 的个数。
public int NumberOf1(int n) {
int cnt = 0;
while (n != 0) {
cnt++;
n &= (n - 1);
}
return cnt;
}
2.Integer.bitCount()方法用于统计二进制中1的个数。
public int NumberOf1(int n) {
return Integer.bitCount(n);
}
15.引申:
1.判断一个整数是不是2的整数次方
以整数如果是2的整数次方,那么它的二进制表示中有且只有一位1,而其他位都是0,。
思想:整数减1之后和自己做与运算,结果为0,则返回true。
2.输入两个整数m和n计算需要改变m的二进制便是中的多少位数才能得到整数n。
思想:1)求两个整数的异或 2)计算结果中的1的个数(采用之前的方法)。
总结一
- 数据结构题目
数组
字符串
链表(频率最高)
树(二叉树)
图
栈(递归)—和队列结合出题,或者和树、图来结合出题
队列(宽度遍历)—和栈结合出题,或者和树、图来结合出题 - 算法
查找(二分查找)
排序(快速排序和归并排序)
回溯法(迷宫以及类似问题)—二维矩阵结合来出题
动态规划
贪婪算法
分析时间复杂度
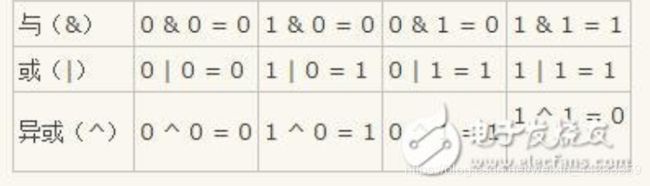
分析问题的重要思想:从上而下的递归思路分析问题,却会基于自下而上的循环实现代码。 - 位运算
二进制的5种运算,与、或、异或、左移、右移
高质量代码
16. 数值的整数次方
17. 打印从 1 到最大的 n 位数
题目描述
输入数字 n,按顺序打印出从 1 到最大的 n 位十进制数。比如输入 3,则打印出 1、2、3 一直到最大的 3 位数即 999。
思想在剑指offer上
要考虑n会出现大数的情况
算法描述:
- ????
字符串模拟数字加法
代码实现:
n位数就是0到9的全排列,即每一位上都是0到9随机的数字,递归结束的条件是我们已经设置了数字的最后一位。
代码实现:
public static void Print1ToMaxOfDigits(int n) {
if(n<=0)
return;
char[] number=new char[n+1];
for (int i = 0; i < 10; i++) {
number[0]=(char) (i+'0');//个位的全排列
PrintToMaxOfNDigitsRecursively(number,n,0);//调用递归
}
}
public static void PrintToMaxOfNDigitsRecursively(char[] number,int length,int index) {
if(index==length-1)//递归结束条件
{
printNumber(number);
return;
}
for (int i = 0; i <10; i++) {
number[index+1]=(char)(i+'0');//下一位的全排列
PrintToMaxOfNDigitsRecursively(number,length,index+1);//进入递归
}
}
public static void printNumber(char[] number) {//打印数字,这里数组左边的0不打印,从第一个非0数字打印
boolean isBeginning=true;
int nLength=number.length;
for (int i = 0; i < nLength; i++) {
if(isBeginning&&number[i]!='0')
isBeginning=false;
if(!isBeginning) {
System.out.print(""+number[i]);
}
}
}
18.1 在 O(1) 时间内删除链表节点
18.2 删除链表中重复的结点
19. 正则表达式匹配
20. 表示数值的字符串
21. 调整数组顺序使奇数位于偶数前面
package Exercise;
public class Solution21 {
public static void reOrderArray(int [] array) {
if(array.length<=1)
return;
int begin=0;
int end=array.length-1;
while(begin22.链表中倒数第k个节点
package Exercise;
//重点是对于输入的判定是否合理,若不合理有什么处理对策
class ListNode {
int val;
ListNode next = null;
ListNode(int val) {
this.val = val;
}
}
public class solution22 {
public static ListNode FindKthToTail(ListNode head,int k) {
if(k<=0||head==null)
return null;
int count=0;
ListNode node=head;
while(node!=null){
count++;
node=node.next;
}
if(count考试中遇到的题
1.最长上升子序列
leetcode解析
给定一个无序的整数数组,找到其中最长上升子序列的长度。
示例:
输入: [10,9,2,5,3,7,101,18]
输出: 4
解释: 最长的上升子序列是 [2,3,7,101],它的长度是 4。
说明:
可能会有多种最长上升子序列的组合,你只需要输出对应的长度即可。
你算法的时间复杂度应该为 O(n2) 。
进阶: 你能将算法的时间复杂度降低到 O(n log n) 吗?
方法一:暴力法
算法:
最简单的方法是找到所有增加的子序列,然后返回最长增加的子序列的最大长度。为了做到这一点,我们使用递归函数 lengthoflis\text length of lislengthoflis 返回从当前元素(对应于 curposcurposcurpos)开始可能的 lis 长度(包括当前元素)。在每个函数调用中,我们考虑两种情况:
- 当前元素大于包含在 lis 中的前一个元素。在这种情况下,我们可以在 lis 中包含当前元素。因此,我们通过将其包含在内,得出了 lis 的长度。此外,我们还通过不在 lis 中包含当前元素来找出 lis 的长度。因此,当前函数调用返回的值是两个长度中的最大值。
- 当前元素小于包含在 lis 中的前一个元素。在这种情况下,我们不能在 lis 中包含当前元素。因此,我们只通过不在 lis 中包含当前元素(由当前函数调用返回)来确定 lis 的长度。
public class Solution {
public int lengthOfLIS(int[] nums) {
return lengthofLIS(nums, Integer.MIN_VALUE, 0);
}
public int lengthofLIS(int[] nums, int prev, int curpos) {
if (curpos == nums.length) {
return 0;
}
int taken = 0;
if (nums[curpos] > prev) {
taken = 1 + lengthofLIS(nums, nums[curpos], curpos + 1);
}
int nottaken = lengthofLIS(nums, prev, curpos + 1);
return Math.max(taken, nottaken);
}
}
复杂度分析

方法二:??带记忆的递归
算法:
在前面的方法中,许多递归调用必须使用相同的参数进行一次又一次的调用。通过将为特定调用获得的结果存储在二维记忆数组 memomemomemo 中,可以消除这种冗余。memo[i][j]memo[i][j]memo[i][j] 表示使用 nums[i]nums[i]nums[i] 作为上一个被认为包含/不包含在 lis 中的元素的 lis 可能的长度,其中 nums[j]nums[j]nums[j] 作为当前被认为包含/不包含在 lis 中的元素。这里,numsnumsnums 表示给定的数组。
public class Solution {
public int lengthOfLIS(int[] nums) {
int memo[][] = new int[nums.length + 1][nums.length];
for (int[] l : memo) {
Arrays.fill(l, -1);
}
return lengthofLIS(nums, -1, 0, memo);
}
public int lengthofLIS(int[] nums, int previndex, int curpos, int[][] memo) {
if (curpos == nums.length) {
return 0;
}
if (memo[previndex + 1][curpos] >= 0) {
return memo[previndex + 1][curpos];
}
int taken = 0;
if (previndex < 0 || nums[curpos] > nums[previndex]) {
taken = 1 + lengthofLIS(nums, curpos, curpos + 1, memo);
}
int nottaken = lengthofLIS(nums, previndex, curpos + 1, memo);
memo[previndex + 1][curpos] = Math.max(taken, nottaken);
return memo[previndex + 1][curpos];
}
}
复杂度分析

方法三:动态规划
https://leetcode-cn.com/problems/longest-increasing-subsequence/solution/dong-tai-gui-hua-er-fen-cha-zhao-tan-xin-suan-fa-p/
- 这个代码方便理解
import java.util.Arrays;
public class Solution {
//【关键】将 dp 数组定义为:以 nums[i] 结尾的最长上升子序列的长度
// 那么题目要求的,就是这个 dp 数组中的最大者
// 以数组 [10, 9, 2, 5, 3, 7, 101, 18] 为例:
// dp 的值: 1 1 1 2 2 3 4 4
// 注意实现细节。
public int lengthOfLIS(int[] nums) {
int len = nums.length;
if (len == 0) {
return 0;
}
// 状态的定义是:以 i 结尾的最长上升子序列的长度
// 状态转移方程:之前比最后那个数字小的最长上升子序列的长度 + 1
int[] dp = new int[len];
// 如果只有 1 个元素,那么这个元素自己就构成了最长上升子序列,所以设置为 1 是合理的
Arrays.fill(dp, 1);
// 从第 2 个元素开始,逐个写出 dp 数组的元素的值
for (int i = 1; i < len; i++) {
int curVal = nums[i];
// 找出比当前元素小的哪些元素的最小值
for (int j = 0; j < i; j++) {
if (curVal > nums[j]) {
dp[i] = Integer.max(dp[j] + 1, dp[i]);
}
}
}
// 最后要全部走一遍,看最大值
int res = dp[0];
for (int i = 0; i < len; i++) {
res = Integer.max(res, dp[i]);
}
return res;
}
public static void main(String[] args) {
int[] nums = {10, 9, 2, 5, 3, 7, 101, 18};
Solution solution = new Solution();
int lengthOfLIS = solution.lengthOfLIS(nums);
System.out.println(lengthOfLIS);
}
}
- 这个代码可以节约空间复杂度
import java.util.Arrays;
public class Solution {
public int lengthOfLIS(int[] nums) {
int len = nums.length;
if (len == 0) {
return 0;
}
int[] dp = new int[len];
Arrays.fill(dp, 1);
int res = 1;
for (int i = 1; i < len; i++) {
for (int j = 0; j < i; j++) {
if (nums[j] < nums[i]) {
dp[i] = Math.max(dp[i], dp[j] + 1);
}
}
res = Math.max(res, dp[i]);
}
return res;
}
}
时间复杂度:O(N^2),因为有两个 for 循环,每个 for 循环的时间复杂度都是线性的。
空间复杂度:O(N),要开和数组等长的状态数组,最后要拉通看一遍状态数组的最大值,因此空间复杂度是 O(N)
方法四:贪心算法+二分查找
https://leetcode-cn.com/problems/longest-increasing-subsequence/solution/dong-tai-gui-hua-er-fen-cha-zhao-tan-xin-suan-fa-p/
1.
public class Solution {
public int lengthOfLIS(int[] nums) {
int len = nums.length;
// 特判
if (len <= 1) {
return len;
}
// tail 数组的定义:长度为 i + 1 的上升子序列的末尾最小是几
int[] tail = new int[len];
// 遍历第 1 个数,直接放在有序数组 tail 的开头
tail[0] = nums[0];
// end 表示有序数组 tail 的最后一个已经赋值元素的索引
int end = 0;
for (int i = 1; i < len; i++) {
// 【逻辑 1】比 tail 数组实际有效的末尾的那个元素还大
if (nums[i] > tail[end]) {
// 直接添加在那个元素的后面,所以 end 先加 1
end++;
tail[end] = nums[i];
} else {
// 使用二分查找法,在有序数组 tail 中
// 找到第 1 个大于等于 nums[i] 的元素,尝试让那个元素更小
int left = 0;
int right = end;
while (left < right) {
// 选左中位数不是偶然,而是有原因的,原因请见 LeetCode 第 35 题题解
// int mid = left + (right - left) / 2;
int mid = left + ((right - left) >>> 1);
if (tail[mid] < nums[i]) {
// 中位数肯定不是要找的数,把它写在分支的前面
left = mid + 1;
} else {
right = mid;
}
}
// 走到这里是因为 【逻辑 1】 的反面,因此一定能找到第 1 个大于等于 nums[i] 的元素
// 因此,无需再单独判断
tail[left] = nums[i];
}
// 调试方法
// printArray(nums[i], tail);
}
// 此时 end 是有序数组 tail 最后一个元素的索引
// 题目要求返回的是长度,因此 +1 后返回
end++;
return end;
}
// 调试方法,以观察是否运行正确
private void printArray(int num, int[] tail) {
System.out.print("当前数字:" + num);
System.out.print("\t当前 tail 数组:");
int len = tail.length;
for (int i = 0; i < len; i++) {
if (tail[i] == 0) {
break;
}
System.out.print(tail[i] + ", ");
}
System.out.println();
}
public static void main(String[] args) {
int[] nums = new int[]{3, 5, 6, 2, 5, 4, 19, 5, 6, 7, 12};
Solution8 solution8 = new Solution8();
int lengthOfLIS = solution8.lengthOfLIS(nums);
System.out.println("最长上升子序列的长度:" + lengthOfLIS);
}
}
- 对1的改进
不分情况,直接二分法查找正确位置。
public class Solution {
public int lengthOfLIS(int[] nums) {
int len = nums.length;
// 特判
if (len <= 1) {
return len;
}
// tail 数组的定义:长度为 i + 1 的上升子序列的末尾最小是几
int[] tail = new int[len];
// 遍历第 1 个数,直接放在有序数组 tail 的开头
tail[0] = nums[0];
// end 表示有序数组 tail 的最后一个已经赋值元素的索引
int end = 0;
for (int i = 1; i < len; i++) {
int left = 0;
// 这里,因为当前遍历的数,有可能比有序数组 tail 数组实际有效的末尾的那个元素还大
// 【逻辑 1】因此 end + 1 应该落在候选区间里
int right = end + 1;
while (left < right) {
// 选左中位数不是偶然,而是有原因的,原因请见 LeetCode 第 35 题题解
// int mid = left + (right - left) / 2;
int mid = (left + right) >>> 1;
if (tail[mid] < nums[i]) {
// 中位数肯定不是要找的数,把它写在分支的前面
left = mid + 1;
} else {
right = mid;
}
}
// 因为 【逻辑 1】,因此一定能找到第 1 个大于等于 nums[i] 的元素
// 因此,无需再单独判断,直接更新即可
tail[left] = nums[i];
// 但是 end 的值,需要更新,当前仅当更新位置在当前 end 的下一位
if (left == end + 1) {
end++;
}
}
// 调试方法
// printArray(nums[i], tail);
// 此时 end 是有序数组 tail 最后一个元素的索引
// 题目要求返回的是长度,因此 +1 后返回
end++;
return end;
}
// 调试方法,以观察是否运行正确
private void printArray(int num, int[] tail) {
System.out.print("当前数字:" + num);
System.out.print("\t当前 tail 数组:");
int len = tail.length;
for (int i = 0; i < len; i++) {
if (tail[i] == 0) {
break;
}
System.out.print(tail[i] + ", ");
}
System.out.println();
}
public static void main(String[] args) {
int[] nums = new int[]{3, 5, 6, 2, 5, 4, 19, 5, 6, 7, 12};
Solution9 solution9 = new Solution9();
int lengthOfLIS = solution9.lengthOfLIS(nums);
System.out.println("最长上升子序列的长度:" + lengthOfLIS);
}
}
复杂度分析:
时间复杂度:O(NlogN),遍历数组使用了O(N),二分查找法使用了O(logN)
空间复杂度:O(N),开辟有序数组tail的空间之多和原始数组一样。
2.二分查找的模板
https://leetcode-cn.com/problems/search-insert-position/solution/te-bie-hao-yong-de-er-fen-cha-fa-fa-mo-ban-python-/
二分查找基本的代码
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
示例 1:
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4
提示:
1. 你可以假设 nums 中的所有元素是不重复的。
2. n 将在 [1, 10000]之间。
3. nums 的每个元素都将在 [-9999, 9999]之间。
x的平方根
方法一:二分法
思路分析:使用二分法搜索平方根的思想很简单,就类似于小时候我们看的电视节目中的“猜价格”游戏,高了就往低了猜,低了就往高了猜,范围越来越小。因此,使用二分法猜算术平方根就很自然。
参考代码 1:所有的数都放在一起考虑,为了照顾到 0把左边界设置为 0,为了照顾到 1 把右边界设置为 x // 2 + 1。
public class Solution {
public int mySqrt(int x) {
// 注意:针对特殊测试用例,例如 2147395599
// 要把搜索的范围设置成长整型
// 为了照顾到 0 把左边界设置为 0
long left = 0;
// # 为了照顾到 1 把右边界设置为 x // 2 + 1
long right = x / 2 + 1;
while (left < right) {
// 注意:这里一定取右中位数,如果取左中位数,代码会进入死循环
// long mid = left + (right - left + 1) / 2;
long mid = (left + right + 1) >>> 1;
long square = mid * mid;
if (square > x) {
right = mid - 1;
} else {
left = mid;
}
}
// 因为一定存在,因此无需后处理
return (int) left;
}
}
Java 代码要注意到:如果中点 mid 声明为 int 类型,针对大整型测试用例通不过,因此变量需要声明为 long 类型,下同。
参考代码 2:事实上,只要单独照顾一下 0 这个特例就可以了。
public class Solution {
public int mySqrt(int x) {
if (x == 0) {
return 0;
}
// 注意:针对特殊测试用例,例如 2147395599
// 要把搜索的范围设置成长整型
long left = 1;
long right = x / 2;
while (left < right) {
// 注意:这里一定取右中位数,如果取左中位数,代码会进入死循环
// long mid = left + (right - left + 1) / 2;
long mid = (left + right + 1) >>> 1;
long square = mid * mid;
if (square > x) {
right = mid - 1;
} else {
left = mid;
}
}
// 因为一定存在,因此无需后处理
return (int) left;
}
}
注意: 这里二分法的使用是有技巧的(如果你没有意识到,这里很可能是个“坑”),下面我就上面注释中提到的:
注意:这里一定取右中位数,如果取左中位数,代码可能会进入死循环。
参考代码 3:干脆我不讨论 a 的边界,让二分法去排除不符合的区间吧,对数级别的时间复杂度对性能不会有很大影响。
public class Solution {
public int mySqrt(int x) {
long left = 0;
long right = Integer.MAX_VALUE;
while (left < right) {
// 这种取中位数的方法又快又好,是我刚学会的,原因在下面这篇文章的评论区
// https://www.liwei.party/2019/06/17/leetcode-solution-new/search-insert-position/
// 注意:这里得用无符号右移
long mid = (left + right + 1) >>> 1;
long square = mid * mid;
if (square > x) {
right = mid - 1;
} else {
left = mid;
}
}
return (int) left;
}
}
方法二:牛顿法
使用牛顿法可以得到一个正实数的算术平方根,因为题目中说“结果只保留整数部分”,因此,我们把使用牛顿法得到的浮点数转换为整数即可。
这里给出牛顿法的思想:
在迭代过程中,以直线代替曲线,用一阶泰勒展式(即在当前点的切线)代替原曲线,求直线与 xxx 轴的交点,重复这个过程直到收敛。

注意:牛顿法得到的是平方根的浮点型精确值(可能会有一定误差),根据题目中的要求,把最后得到的这个数转换为 int 型,即去掉小数部分即可。
牛顿法的应用:一个是求方程的根,另一个是求解最优化问题
public class Solution {
public int mySqrt(int a) {
long x = a;
while (x * x > a) {
x = (x + a / x) / 2;
}
return (int) x;
}
}
说明:1e-6 是科学计数法,表示 1乘以 10的负 6 次方,也就是0.000001。有的地方使用 epsilon(ϵ)表示 1e-6 ,用来抵消浮点运算中因为误差造成的相等无法判断的情况,它通常是一个非常小的数字,具体多小要根据你的精度需求来设置。
寻找旋转排序数组中的最小值(不存在重复元素)
https://leetcode-cn.com/problems/find-minimum-in-rotated-sorted-array/solution/er-fen-fa-fen-zhi-fa-python-dai-ma-java-dai-ma-by-/
假设按照升序排序的数组在预先未知的某个点上进行了旋转。
( 例如,数组 [0,1,2,4,5,6,7] 可能变为 [4,5,6,7,0,1,2] )。
请找出其中最小的元素。
你可以假设数组中不存在重复元素。
示例 1:
输入: [3,4,5,1,2]
输出: 1
方法一:二分搜索
/************再想一想
思想:
由于给定的数组是有序的,我们就可以使用二分搜索。然而,数组被旋转了,所以简单的使用二分搜索并不可行。
在这个问题中,我们使用一种改进的二分搜索,判断条件与标准的二分搜索有些不同。
在这个改进版本的二分搜索算法中,我们需要找到这个点。下面是关于变化点的特点:
所有变化点左侧元素 > 数组第一个元素
所有变化点右侧元素 < 数组第一个元素
算法:
1. 找到数组的中间元素 mid。
2. 如果中间元素 > 数组第一个元素,我们需要在 mid 右边搜索变化点。
3. 如果中间元素 < 数组第一个元素,我们需要在 mid 做边搜索变化点。
4. 当我们找到变化点时停止搜索,当以下条件满足任意一个即可:
**nums[mid] > nums[mid + 1],因此 mid+1 是最小值。
nums[mid - 1] > nums[mid],因此 mid 是最小值。**
*********************/
public class Solution {
public int findMin(int[] nums) {
int len = nums.length;
if (len == 0) {
throw new IllegalArgumentException("数组为空,无最小元素");
}
int left = 0;
int right = len - 1;
while (left < right) {
// int mid = left + (right - left) / 2;
int mid = (left + right) >>> 1;
if (nums[mid] > nums[right]) {
left = mid + 1;
} else {
// 因为题目中说:你可以假设数组中不存在重复元素。
// 此时一定有 nums[mid] < nums[right]
right = mid;
}
}
// 一定存在最小元素,因此无需再做判断
return nums[left];
}
}
方法二:分治法
把原问题分解成若干的小问题,小问题解决了,原问题就解决了。典型的例子是归并法和快排序。
public class Solution {
// 虽然可以通过,但是时间复杂度是 O(n)
public int findMin(int[] nums) {
int len = nums.length;
if (len == 0) {
throw new IllegalArgumentException("数组为空");
}
return findMin(nums, 0, len - 1);
}
private int findMin(int[] nums, int left, int right) {
// 思考:这个临界条件是为什么?
// 或者写成 left + 1 >= right
if (left == right || left + 1 == right) {
return Math.min(nums[left], nums[right]);
}
// int mid = left + (right - left) / 2;
int mid = (left + right) >>> 1;
// 8 9 1 2 3 4 5 6 7
if (nums[mid] < nums[right]) {
// 右边是顺序数组
return Math.min(findMin(nums, left, mid - 1), nums[mid]);
} else {
// 左边是顺序数组
// nums[mid] > nums[right]
// 3 4 5 6 7 8 1 2
return Math.min(nums[left], findMin(nums, mid + 1, right));
}
}
public static void main(String[] args) {
Solution2 solution2 = new Solution2();
int[] nums = {1, 2};
int solution2Min = solution2.findMin(nums);
System.out.println(solution2Min);
}
}
寻找旋转排序数组中的最小值||(存在重复元素)
https://leetcode-cn.com/problems/find-minimum-in-rotated-sorted-array-ii/description/
方法一:二分法
注意:这里的提法是“中间数”,即位于中间的那个数,不是中位数,请注意区分。
可以分为以下两种情况:
1、中间数与左边界比较
尝试在纸上写出几个例子:
例 1:[1, 2, 3, 4, 5]
例 2:[2, 3, 4, 5, 1]
以上这两个例子,中间数都比左边界大,但是旋转排序数组的最小值可能在中间数的左边(例 1),也可能在中间数的右边(例 2),因此不能使用中间数与左边界比较作为二分法的讨论依据。
2、中间数与右边界比较:
(1)当中间数比右边界表示的数大的时候,中间数就一定不是目标数(旋转排序数组的最小值)。
还是尝试举个例子:
例 3:[7, 8, 9, 10, 11, 12, 1, 2, 3]
中间数 11 比右边界 3 大,因此中间数以及中间数前面的数都不是目标数,把左边界设置中间数位置 + 1,即 left = mid + 1;
(2)当中间数比右边界表示的数小的时候,中间数就可能是目标数(旋转排序数组的最小值),举个例子:
例 4:[7, 8, 1, 2, 3]
中间数 1 比右边界表示的数小的时候,说明,中间数到右边界是递增的(对于这道题是非递减),那么中间数右边的(不包括中间数)就一定不是目标数,可以把它们排除,不过中间数有可能是目标数,就如本例,因此,把右边界设置为 right = mid。
(3)当中间数与右边界表示的数相等的时候,看下面两个例子:
例 5:[0, 1, 1, 1, 1, 1, 1]
例 6:[1, 1, 1, 1, 0, 1, 1]
目标值可能在中间数的左边,也可能在中间数的右边,那么该怎么办呢?很简单,此时你看到的是右边界,就把只右边界排除掉就好了。正是因为右边界和中间数相等,你去掉了右边界,中间数还在,就让中间数在后面的循环中被发现吧。
因此,根据中间数和右边界的大小关系,可以使用二分法搜索到目标值。
关键:
解本题的关键在于举例,在尝试举例的过程中,考虑到不同的情况,得到解题思路。
代码实现:
public class Solution {
public int findMin(int[] nums) {
int len = nums.length;
if (len == 0) {
return 0;
}
int left = 0;
int right = len - 1;
while (left < right) {
// int mid = left + (right - left) / 2;
int mid = (left + right) >>> 1;
if (nums[mid] > nums[right]) {
left = mid + 1;
} else if (nums[mid] < nums[right]) {
right = mid;
} else {
right--;
}
}
return nums[left];
}
}
方法二:分治法
同上一题
public class Solution {
public int findMin(int[] nums) {
int len = nums.length;
if (len == 0) {
throw new IllegalArgumentException("数组为空,最小值不存在");
}
return findMin(nums, 0, len - 1);
}
private int findMin(int[] nums, int left, int right) {
if (left + 1 >= right) {
return Math.min(nums[left], nums[right]);
}
if (nums[left] < nums[right]) {
return nums[left];
}
// int mid = left + (right - left) / 2;
int mid = (left + right) >>> 1;
return Math.min(findMin(nums, left, mid - 1), findMin(nums, mid, right));
}
}
寻找重复数
https://leetcode-cn.com/problems/find-the-duplicate-number/solution/er-fen-fa-si-lu-ji-dai-ma-python-by-liweiwei1419/
给定一个包含 n + 1 个整数的数组 nums,其数字都在 1 到 n 之间(包括 1 和 n),可知至少存在一个重复的整数。假设只有一个重复的整数,找出这个重复的数。
示例 1:
输入: [1,3,4,2,2]
输出: 2
示例 2:
输入: [3,1,3,4,2]
输出: 3
说明:
- 不能更改原数组(假设数组是只读的)。
- 只能使用额外的 O(1) 的空间。
- 时间复杂度小于 O(n^2) 。
- 数组中只有一个重复的数字,但它可能不止重复出现一次。
- 思路分析:
如果题目不限制:
1、不能更改原数组(假设数组是只读的);
2、只能使用额外的 O(1) 的空间。
容易想到的方法有:
(1)使用哈希表判重,这违反了限制 2;
(2)排序以后,重复的数相邻,这违反了限制 1;
(3)使用桶排序,当两个数发现要放在同一个地方的时候,就发现了这个重复的元素,这违反了限制 1;
(4)既然要定位数,可以对“数”做二分,但是比较恶心的一点是得反复看整个数组好几次,于是就有下面的二分法,本文就介绍通过二分法定位数;
(5)还可以使用“快慢指针”来完成,不过这种做法太有技巧性了,不是通用的做法,大家可以在评论区和题解区看到。
方法:二分法
关键:这道题的关键是对要定位的“数”做二分,而不是对数组的索引做二分。要定位的“数”根据题意在 11 和 nn 之间,每一次二分都可以将搜索区间缩小一半。
以 [1, 2, 2, 3, 4, 5, 6, 7] 为例,一共有 88 个数,每个数都在 11 和 77 之间。11 和 77 的中位数是 44,遍历整个数组,统计小于 44 的整数的个数,至多应该为 33 个,如果超过 33 个就说明重复的数存在于区间 [1,4)[1,4) (注意:左闭右开)中;否则,重复的数存在于区间 [4,7][4,7](注意:左右都是闭)中。这里小于 44 的整数有 44 个(它们是 1, 2, 2, 3),因此砍掉右半区间,连中位数也砍掉。以此类推,最后区间越来越小,直到变成 11 个整数,这个整数就是我们要找的重复的数。
参考代码 1:
public class Solution {
public int findDuplicate(int[] nums) {
int len = nums.length;
int left = 1;
int right = len - 1;
while (left < right) {
// int mid = left + (right - left) / 2;
int mid = (left + right) >>> 1;
int counter = 0;
for (int num : nums) {
if (num <= mid) {
counter += 1;
}
}
if (counter > mid) {
right = mid;
} else {
left = mid + 1;
}
}
return left;
}
}
复杂度分析:
- 时间复杂度:O(NlogN),二分法的时间复杂度为 O(logN),在二分法的内部,执行了一次 for 循环,时间复杂度为 O(N),故时间复杂度为O(NlogN)。
- 空间复杂度:O(1),使用了一个 count 变量,因此空间复杂度为 O(1)。
山脉数组中查找目标值
https://leetcode-cn.com/problems/find-in-mountain-array/
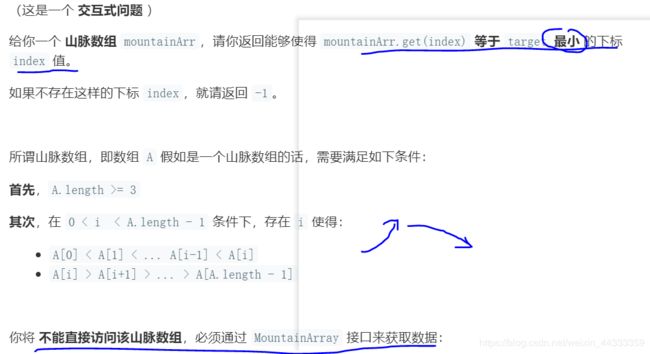

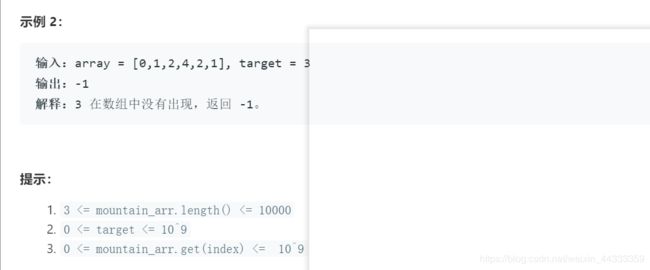

方法:二分查找法
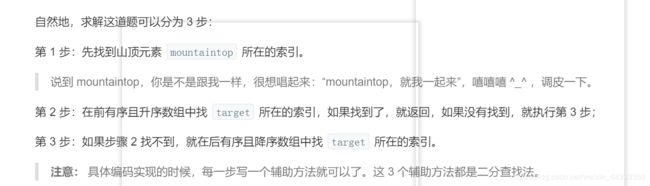
/**
* // This is MountainArray's API interface.
* // You should not implement it, or speculate about its implementation
*/
interface MountainArray {//接口
public int get(int index);
public int length();
}
class MountainArrayImpl implements MountainArray {//继承接口并实现接口方法
private int[] arr;
private int size;
public MountainArrayImpl(int[] arr) {//构造方法
this.arr = arr;
this.size = this.arr.length;
}
@Override
public int get(int index) {//返回下标为index的数组元素
return this.arr[index];
}
@Override
public int length() {//数组长度
return this.size;
}
}
class Solution {
// 特别注意:3 个辅助方法的分支出奇地一样,因此选中位数均选左中位数,才不会发生死循环
public int findInMountainArray(int target, MountainArray mountainArr) {
int size = mountainArr.length();
// 步骤 1:先找到山顶元素所在的索引
int mountaintop = findMountaintop(mountainArr, 0, size - 1);
// 步骤 2:在前有序且**升序**数组中找 target 所在的索引
int res = findFromSortedArr(mountainArr, 0, mountaintop, target);
if (res != -1) {
return res;
}
// 步骤 3:如果步骤 2 找不到,就在后有序且**降序**数组中找 target 所在的索引
return findFromInversedArr(mountainArr, mountaintop + 1, size - 1, target);
}
private int findMountaintop(MountainArray mountainArr, int l, int r) {
// 返回山顶元素
while (l < r) {
int mid = (r +l) >>>1;
// 取左中位数,因为进入循环,数组一定至少有 2 个元素
// 因此,左中位数一定有右边元素,数组下标不会发生越界
if (mountainArr.get(mid) < mountainArr.get(mid + 1)) {
// 如果当前的数比右边的数小,它一定不是山顶
l = mid + 1;
} else {
r = mid;
}
}
// 根据题意,山顶元素一定存在,因此退出 while 循环的时候,不用再单独作判断
return l;
}
private int findFromSortedArr(MountainArray mountainArr, int l, int r, int target) {
// 在前有序且**升序**数组中找 target 所在的索引
while (l < r) {
int mid = (r +l) >>>1;
if (mountainArr.get(mid) < target) {//在升序数组找目标数据
l = mid + 1;
} else {
r = mid;
}
}
// 因为不确定区间收缩成 1个数以后,这个数是不是要找的数,因此单独做一次判断
if (mountainArr.get(l) == target) {
return l;
}
return -1;
}
private int findFromInversedArr(MountainArray mountainArr, int l, int r, int target) {
// 在后有序且**降序**数组中找 target 所在的索引
while (l < r) {
int mid = (r +l) >>>1;
// 与 findFromSortedArr 方法不同的地方仅仅在于由原来的小于号改成大于好
if (mountainArr.get(mid) > target) {//在降序数组找目标数据
l = mid + 1;
} else {
r = mid;
}
}
// 因为不确定区间收缩成 1个数以后,这个数是不是要找的数,因此单独做一次判断
if (mountainArr.get(l) == target) {
return l;
}
return -1;
}
public static void main(String[] args) {//测试用例
int[] arr = {1, 2, 3, 4, 5, 3, 1};
int target = 3;
MountainArray mountainArray = new MountainArrayImpl(arr);
Solution solution = new Solution();
int res = solution.findInMountainArray(target, mountainArray);
System.out.println(res);
}
}
找到 K 个最接近的元素
https://leetcode-cn.com/problems/find-k-closest-elements/


方法一:排除法(双指针)
import java.util.ArrayList;
import java.util.List;
public class Solution {
public List findClosestElements(int[] arr, int k, int x) {
int size = arr.length;
int left = 0;
int right = size - 1;
int removeNums = size - k;
while (removeNums > 0) {
if (x - arr[left] <= arr[right] - x) {
right--;
} else {
left++;
}
removeNums--;
}
List res = new ArrayList<>();
for (int i = left; i < left + k; i++) {
res.add(arr[i]);
}
return res;
}
public static void main(String[] args) {
int[] arr = {0, 0, 1, 2, 3, 3, 4, 7, 7, 8};
int k = 3;
int x = 5;
Solution solution = new Solution();
List res = solution.findClosestElements(arr, k, x);
System.out.println(res);
}
}
3.判断s1字符串的全排列是否包含在s2中 Permutation in String
详情1
leetcode
算法描述:
给定两个字符串 s1 和 s2,写一个函数来判断 s2 是否包含 s1 的排列。
换句话说,第一个字符串的排列之一是第二个字符串的子串。
示例1:
输入: s1 = "ab" s2 = "eidbaooo"
输出: True
解释: s2 包含 s1 的排列之一 ("ba").
注意:
- 输入的字符串只包含小写字母
- 两个字符串的长度都在 [1, 10,000] 之间
解决:
① 给定两个字符串s1和s2,问我们s1的全排列的字符串任意一个是否为s2的字串。
虽然题目中有全排列的关键字,但是跟之前的全排列的题目的解法并不一样,如果受思维定势影响比较深的话,很容易遍历s1所有全排列的情况,然后检测其是否为s2的子串,这种解法是非常不高效的,本题本质上可以转换为求在一定范围内(s1长度),字符与s1字符相同的情况是否存在于字符串s2内。
使用滑动窗口Sliding Window的思想来做:
我们先来分别统计s1和s2中前n1个字符串中各个字符出现的次数,其中n1为字符串s1的长度,这样如果二者字符出现次数的情况完全相同,说明s1和s2中前n1的字符互为全排列关系,那么符合题意了,直接返回true。如果不是的话,那么我们遍历s2之后的字符,对于遍历到的字符,对应的次数加1,由于窗口的大小限定为了n1,所以每在窗口右侧加一个新字符的同时就要在窗口左侧去掉一个字符,每次都比较一下两个哈希表的情况,如果相等,说明存在。
class Solution { //26ms
public boolean checkInclusion(String s1, String s2) {
int len1 = s1.length();
int len2 = s2.length();
if(len1 > len2) return false;
int[] h1 = new int[256];
int[] h2 = new int[256];
for (int i = 0;i < len1;i ++){
h1[s1.charAt(i)] ++;
h2[s2.charAt(i)] ++;
}
if (Arrays.equals(h1,h2)) return true;
for (int i = len1;i < len2;i ++){
h2[s2.charAt(i)] ++;
h2[s2.charAt(i - len1)] --;
if (Arrays.equals(h1,h2)) return true;
}
return false;
}
}
② 滑动窗口+hash table + 双指针?????
class Solution { //15ms
public boolean checkInclusion(String s1, String s2) {
int len1 = s1.length();
int len2 = s2.length();
if(len1 > len2) return false;
int[] hash = new int[256];
for (char c : s1.toCharArray()){
hash[c] ++;
}
int count = len1;
char[] schar = s2.toCharArray();
int left = 0;
int right = 0;
while(right < len2){
if (hash[schar[right ++]] -- > 0) count --;
while(count == 0){
if (right - left == len1) return true;
if (hash[schar[left ++]] ++ == 0) count ++;
}
}
return false;
}
}
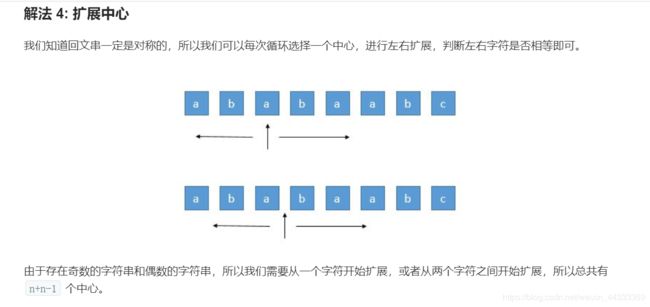
最长回文串
public String longestPalindrome(String s) {
if (s == null || s.length() < 1) return " ";
int start = 0, end = 0;
for (int i = 0; i < s.length(); i++) {
int len1 = expandAroundCenter(s, i, i);//以i为中心,求奇数串的回文串长度
int len2 = expandAroundCenter(s, i, i + 1);//偶数串,从i和i+1开始中间到两边判断回文串。
int len = Math.max(len1, len2);//求以奇偶串求出的回文串长度的最大者
if (len > end - start) {//更新回文串最长的范围
start = i - (len - 1) / 2;
end = i + len / 2;
}
}
return s.substring(start, end + 1);
}
private int expandAroundCenter(String s, int left, int right) {
int L = left, R = right;
while (L >= 0 && R < s.length() && s.charAt(L) == s.charAt(R)) {
L--;
R++;
}
return R - L - 1;
}
求两个数的二进制有多少位不同
关键问题是怎么求一个数的二进制中的1的个数
几个典型的求二进制数的1的个数方法
方法1:
向右位移操作也相当于二进制的除2操作,对二进制的最右边一位和1进行与操作,判断1的个数。
以10100010为例:
第一次,和00000001与操作,得到0,向右位移。
第二次,和00000001与操作,得到1,向右位移。
int run(int n)
{
int count = 0;
while (n)
{
count += n & 1;
n >>= 1;
}
return count;
}
方法2:
/**
* 求两个数的二进制中不同的位数
* @param m
* @param n
* @return 返回不同的位数的个数
*/
public static int countBitDiff(int m, int n) {
//异或
int ans = m^n;
//求ans中1的个数
int count = 0;
while(ans != 0){
ans &= (ans -1);
count++;
}
return count;
}
由整数对(父节点和子节点的关系)组成的二叉树的高度问题
问题描述:
现在有一颗合法的二叉树,树的节点都是数字表示,现在给定这棵树上所有的父子关系,求这棵树的高度。
输入的第一行表示节点个数为n,节点的编号为0到n-1组成,下面是n-1行,每行有两个整数,第一个数表示父节点的编号,第二个数表示子节点的编号
输出树的高度,为一个整数。
样例输入:
5
0 1
0 2
1 3
1 4
样例输出: 3
解答思路:
创建一个map<节点,所在的层>,那么map的values中的最大值即为二叉树的高度。
import java.util.*;
public class Main {
public static void main(String[] args) {
Scanner in = new Scanner(System.in);
while (in.hasNextInt()) {
Map map = new HashMap<>();
int n = in.nextInt();
for (int i = 0; i values = map.values();
int max = 0;
for (int value : values){
if (value>0){
max = value;
}
}
System.out.println(max);
}
}
}