史上最详细详解hashmap、concurrenthashmap
本文详述Java语言中的hashmap与concurrenthashmap,使用其他语言的朋友可做参考
首先我们先来看一下这几个类原码开头的部分
public class HashMap extends AbstractMap
implements Map, Cloneable, Serializable public class ConcurrentHashMap extends AbstractMap
implements ConcurrentMap, Serializable
public interface ConcurrentMap extends Map public class TreeMap
extends AbstractMap
implements NavigableMap, Cloneable, java.io.Serializable
public interface NavigableMap extends SortedMap
public interface SortedMap extends Map 我们可以看到,其实这几个类底层都是实现了map接口或者继承了map的子接口,所以我们可以先来看一下map接口里面都有什么?
里面有一个非常重要的内部接口Entry,这个类的格式是key-value键值对,也就是hashmap、concurrenthashmap这两个类的底层数据类型
interface Entry {
K getKey();
V getValue();
V setValue(V value);
boolean equals(Object o);
int hashCode();
public static , V> Comparator> comparingByKey() {
return (Comparator> & Serializable)
(c1, c2) -> c1.getKey().compareTo(c2.getKey());
}
public static > Comparator> comparingByValue() {
return (Comparator> & Serializable)
(c1, c2) -> c1.getValue().compareTo(c2.getValue());
}
public static Comparator> comparingByKey(Comparator cmp) {
Objects.requireNonNull(cmp);
return (Comparator> & Serializable)
(c1, c2) -> cmp.compare(c1.getKey(), c2.getKey());
}
public static Comparator> comparingByValue(Comparator cmp) {
Objects.requireNonNull(cmp);
return (Comparator> & Serializable)
(c1, c2) -> cmp.compare(c1.getValue(), c2.getValue());
}
} 分析完map接口,我们来详细聊一下这三个类
hashmap
hashmap也叫散列表,故名思义,这个数据结构想要将内部存储的数据都散开,越分散越好,最好同一个位置只有1个或0个数据,这样时间复杂度就是完美的O(1)
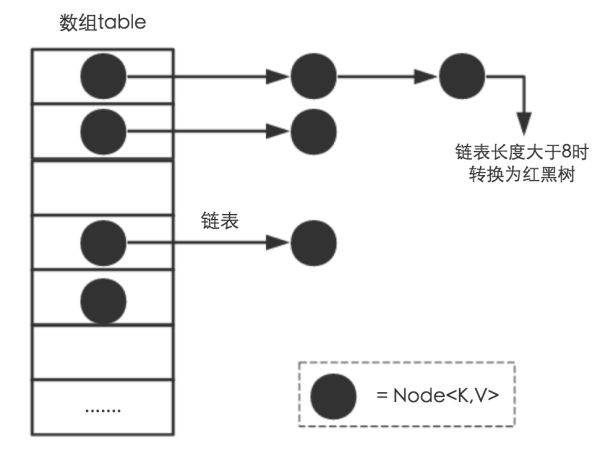
结构
Java1.8之前,hashmap的结构是数组+链表,1.8之后是数组+链表+红黑树,每一个数组的单位会存储一个链表或者红黑树,当链表长度>=8的时候,链表会转化为红黑树,红黑树节点数<=6的时候,红黑树会转化为链表
那么为什么java1.8要新加红黑树这样一个结构呢?
对链表进行操作的时间复杂度为O(n),你需要从头往后挨个节点遍历,时间消耗较高
红黑树是一种特殊的二叉树,时间复杂度为O(logn),能够极大的优化查询速度,不过作者个人认为红黑树出现概率很小,原因下文解释
那么怎么确定一个key放到那个数组里或者从哪里取呢 ?
首先我们先用key的hashcode值的高16位与低16位做一次按位异或操作(函数扰动)计算出一个 hash值,然后使用这个hash值和n-1(n为数组长度,因为hashmap每次扩容都为原来的2倍,所以数组长度一直是2的幂次方,所以n-1通常是后几位全1)做一次按位与操作,由此,取最后几位,得出一个数组下标,即这个key-value应该存在这个桶(桶的概念就是例如有一个长度为4的数组,将每一个数组元素都比喻为一个桶,也就是有4个桶)中
取得话也是同理,计算出数组下标之后,根据key在链表或红黑树里找到相应的value
//hashmap实现hash值原码
static final int hash(Object key) {
int h;
return (key == null) ? 0 : (h = key.hashCode()) ^ (h >>> 16);
}为什么要这么做呢?
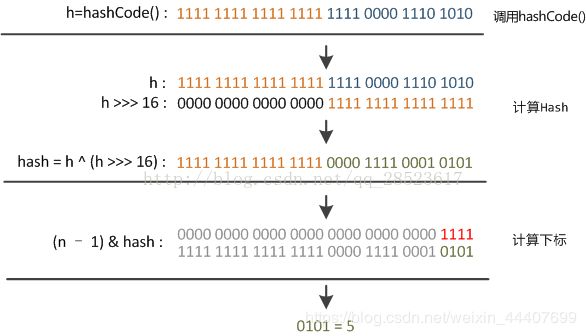
那么为什么要在计算下标之前加一次函数扰动呢?看下图
如果不经过函数扰动,(n-1)的后几位为1,前面全0,与操作其实就变成了后面少数的几位的计算,如果hashcode算法不好的情况,造成哈希碰撞的可能性就会比较大,哈市碰撞多了,大量数据都放在一个或少数几个桶内,显然与散列的主义相违背,所以设计者想要让高16位也能参与到运算中,这样后几位数据的随机性会更大,减少很多数据堆在一个桶内的情况出现的概率。
扩容
hashmap的扩容机制是每次都扩充为原来的两倍(如果长度为0的特殊情况,就扩容为16)为什么数组扩容要为两倍下文详细解释,hashmap里面有一个扩容因子为0.75,当目前的数据总量大于数组长度*扩容因子时数组长度就会扩容为原来的两倍
举例:当数组长度为16时,16*0.75=12,一旦数据总量大于12(即最小为13),数组长度扩容为32
那么会出现一个新问题
数组扩容之后,数据怎么办呢?
很简单,数据根据新的(n-1)重新计算一下下标,也就是进行一次rehash操作,放入相应的桶内。
接下来我们就可以详细的探讨一下前面遗留的几个问题
1、为什么作者认为红黑树出现的可能性很小
首先我们了解到当链表长度>=8的时候,链表转化为红黑树,那么回归到hashmap的初衷,想要将数据散列在不同的桶中,以达到时间复杂度O(1)的目标,为此,还专门设计了函数扰动确保其尽可能的散列,同时,数据总量大于12时,数组会扩容,那么我们做一个假设,在数据总量<=12时,经过函数扰动后还有至少8个数放在同一个桶内。这种情况我认为出现概率是极小的,这个例子仅供大家理解,因为在源码中转换红黑树还有一个条件是数据总量大于等于64,否则扩容!!!!
2、为什么扩容一定要为2倍呢?
因为2的幂次方在二进制的表达中可以保证后几位均为1,为什么要这样做呢?举一个例子就很清楚了,基于按位与操作的思想,两数都为1才为一,若数组长度为15,(15-1)即14表示的话就是1110,1110&1110和1110&1111的结果是相同的,这不就增加了哈希碰撞的概率了嘛,因此,保持n-1的后几位为1,就可以根据hash值的后几位来判别应该放在哪个桶里了
解决hash冲突的 方法
1、开放定址法
当出现hash冲突,他会基于当前下标再去寻找一个不冲突的地址,有线性探测(顺序向后找)、二次探测(根据距离左边找一个、右边找一个)、伪随机探测(建立一个伪随机数发生器,并指定一个随机开始位置,不常见)三种
缺点:hash冲突较多的时候,会浪费大量时间在寻址上
2、链地址法
数组内存放链表,依次链接(hashmap中使用)
3、再哈希法
产生冲突,再通过另一种hash算法计算,直到不产生冲突
缺点:计算时间较长
4、建立公共溢出区
将哈希表分为基本表和溢出表两部分,凡是和基本表发生冲突的元素,一律填入溢出表
缺点:当溢出表存在多个hash冲突的时候,作者不了解溢出表的结构,也没有找到相关资料,猜想它的查询可能会比较慢
为什么hashmap线程不安全
同样举个栗子!d=====( ̄▽ ̄*)b
当线程1put一个值,hashmap扩容了,而线程2还按照原来表的结构去搭建一个逻辑,比如本来0->1,扩容后变为了1->0,可是线程2仍然认为0->1,于是就出现了一个闭环,因此乘hashmap线程不安全
这位朋友讲的非常详细而且有图,大家可以去看一下:https://blog.csdn.net/loveliness_peri/article/details/81092360
那么什么线程安全呢?
hashtable和concurrenthashmap
hashtable由于用synchronized锁了整个表,导致其性能十分低下,用的也越来越少,就不再赘述
concurrenthashmap
concurrenthashmap的结构与hashmap几乎相同,不同的就是保证了线程安全,作者在此就和大家探讨一下如何保证线程安全的问题
Java1.8之前
Java1.8之前,它是通过分段锁来保证线程安全,刚才我们分析了hashmap线程不安全主要是因为put()操作,那么concurrenthashmap就将要放入的数据分为多个Segment,将需要修改的Segment加锁,实现线程安全
于是乎有个疑问,这个Segment咋实现的?
它继承了ReentrantLock,具备锁和释放锁的功能。ConcurrentHashMap只有16个Segment,并且不会扩容,最多可以支持16个线程并发写。
Java1.8之后、
抛弃了Segment这个概念,使用CAS+synchronized来保证线程安全,主要就是对put方法和扩容方法加锁
//put方法具体实现
final V putVal(K key, V value, boolean onlyIfAbsent) {
if (key == null || value == null) throw new NullPointerException();
int hash = spread(key.hashCode());
int binCount = 0;
for (Node[] tab = table;;) {
Node f; int n, i, fh;
if (tab == null || (n = tab.length) == 0)
tab = initTable();
else if ((f = tabAt(tab, i = (n - 1) & hash)) == null) {
if (casTabAt(tab, i, null,
new Node(hash, key, value, null)))
break; // no lock when adding to empty bin
}
else if ((fh = f.hash) == MOVED)
tab = helpTransfer(tab, f);
else {
V oldVal = null;
synchronized (f) {
if (tabAt(tab, i) == f) {
if (fh >= 0) {
binCount = 1;
for (Node e = f;; ++binCount) {
K ek;
if (e.hash == hash &&
((ek = e.key) == key ||
(ek != null && key.equals(ek)))) {
oldVal = e.val;
if (!onlyIfAbsent)
e.val = value;
break;
}
Node pred = e;
if ((e = e.next) == null) {
pred.next = new Node(hash, key,
value, null);
break;
}
}
}
else if (f instanceof TreeBin) {
Node p;
binCount = 2;
if ((p = ((TreeBin)f).putTreeVal(hash, key,
value)) != null) {
oldVal = p.val;
if (!onlyIfAbsent)
p.val = value;
}
}
}
}
if (binCount != 0) {
if (binCount >= TREEIFY_THRESHOLD)
treeifyBin(tab, i);
if (oldVal != null)
return oldVal;
break;
}
}
}
addCount(1L, binCount);
return null;
} 关于扩容方面的代码作者还没有深入读,代码在下面,大家可自行研究一下
//扩容方法
private final void transfer(Node[] tab, Node[] nextTab) {
int n = tab.length, stride;
if ((stride = (NCPU > 1) ? (n >>> 3) / NCPU : n) < MIN_TRANSFER_STRIDE)
stride = MIN_TRANSFER_STRIDE; // subdivide range
if (nextTab == null) { // initiating
try {
@SuppressWarnings("unchecked")
Node[] nt = (Node[])new Node[n << 1];
nextTab = nt;
} catch (Throwable ex) { // try to cope with OOME
sizeCtl = Integer.MAX_VALUE;
return;
}
nextTable = nextTab;
transferIndex = n;
}
int nextn = nextTab.length;
ForwardingNode fwd = new ForwardingNode(nextTab);
boolean advance = true;
boolean finishing = false; // to ensure sweep before committing nextTab
for (int i = 0, bound = 0;;) {
Node f; int fh;
while (advance) {
int nextIndex, nextBound;
if (--i >= bound || finishing)
advance = false;
else if ((nextIndex = transferIndex) <= 0) {
i = -1;
advance = false;
}
else if (U.compareAndSwapInt
(this, TRANSFERINDEX, nextIndex,
nextBound = (nextIndex > stride ?
nextIndex - stride : 0))) {
bound = nextBound;
i = nextIndex - 1;
advance = false;
}
}
if (i < 0 || i >= n || i + n >= nextn) {
int sc;
if (finishing) {
nextTable = null;
table = nextTab;
sizeCtl = (n << 1) - (n >>> 1);
return;
}
if (U.compareAndSwapInt(this, SIZECTL, sc = sizeCtl, sc - 1)) {
if ((sc - 2) != resizeStamp(n) << RESIZE_STAMP_SHIFT)
return;
finishing = advance = true;
i = n; // recheck before commit
}
}
else if ((f = tabAt(tab, i)) == null)
advance = casTabAt(tab, i, null, fwd);
else if ((fh = f.hash) == MOVED)
advance = true; // already processed
else {
synchronized (f) {
if (tabAt(tab, i) == f) {
Node ln, hn;
if (fh >= 0) {
int runBit = fh & n;
Node lastRun = f;
for (Node p = f.next; p != null; p = p.next) {
int b = p.hash & n;
if (b != runBit) {
runBit = b;
lastRun = p;
}
}
if (runBit == 0) {
ln = lastRun;
hn = null;
}
else {
hn = lastRun;
ln = null;
}
for (Node p = f; p != lastRun; p = p.next) {
int ph = p.hash; K pk = p.key; V pv = p.val;
if ((ph & n) == 0)
ln = new Node(ph, pk, pv, ln);
else
hn = new Node(ph, pk, pv, hn);
}
setTabAt(nextTab, i, ln);
setTabAt(nextTab, i + n, hn);
setTabAt(tab, i, fwd);
advance = true;
}
else if (f instanceof TreeBin) {
TreeBin t = (TreeBin)f;
TreeNode lo = null, loTail = null;
TreeNode hi = null, hiTail = null;
int lc = 0, hc = 0;
for (Node e = t.first; e != null; e = e.next) {
int h = e.hash;
TreeNode p = new TreeNode
(h, e.key, e.val, null, null);
if ((h & n) == 0) {
if ((p.prev = loTail) == null)
lo = p;
else
loTail.next = p;
loTail = p;
++lc;
}
else {
if ((p.prev = hiTail) == null)
hi = p;
else
hiTail.next = p;
hiTail = p;
++hc;
}
}
ln = (lc <= UNTREEIFY_THRESHOLD) ? untreeify(lo) :
(hc != 0) ? new TreeBin(lo) : t;
hn = (hc <= UNTREEIFY_THRESHOLD) ? untreeify(hi) :
(lc != 0) ? new TreeBin(hi) : t;
setTabAt(nextTab, i, ln);
setTabAt(nextTab, i + n, hn);
setTabAt(tab, i, fwd);
advance = true;
}
}
}
}
}
} Java1.8为啥要这么做呢?
- 减少内存开销
假设使用ReentrantLock可重入锁,那么每个节点都需要继承AQS,但并不是每个节点都需要同步支持,只有链表的头节点(红黑树的根节点)需要同步,这无疑消耗巨大内存。 - 获得JVM的支持
可重入锁毕竟是API级别的,后续的性能优化空间很小。synchronized则是JVM直接支持的,JVM能够在运行时作出相应的优化措施:锁粗化、锁消除、锁自旋等等。使得synchronized能够随着JDK版本的升级而不改动代码的前提下获得性能上的提升。
至此,我们今天的学习结束
如果作者有什么错误欢迎大家指正,我们共同进步