Octave卷积学习笔记
本文首发于个人博客
Octave卷积
Octave卷积的主题思想来自于图片的分频思想,首先认为图像可进行分频:
- 低频部分:图像低频部分保存图像的大体信息,信息数据量较少
- 高频部分:图像高频部分保留图像的细节信息,信息数据量较大
由此,认为卷积神经网络中的feature map也可以进行分频,可按channel分为高频部分和低频部分,如图所示:
对于一个feature map,将其按通道分为两个部分,分别为低频通道和高频通道。随后将低频通道的长宽各缩减一半,则将一个feature map分为了高频和低频两个部分,即为Octave卷积处理的基本feature map,使用X表示,该类型X可表示为 X = [ X H , X L ] X = [X^H,X^L] X=[XH,XL],其中 X H X^H XH为高频部分, X L X^L XL为低频部分。
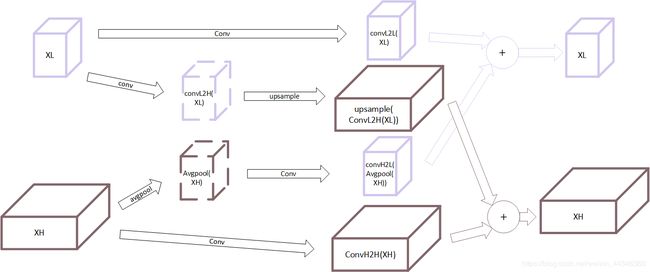
为了处理这种结构的feature map,其使用了如下所示的Octave卷积操作:
首先考虑低频部分输入 X L X^L XL,该部分进行两个部分的操作:
- X L → X H X^L \to X^H XL→XH:从低频到高频,首先使用指定卷积核 W L → H W^{L \to H} WL→H进行卷积,随后进行Upample操作生成与高频部分长宽相同的Tensor,最终产生 Y L → H = U p s a m p l e ( C o n v ( X L , W L → H ) , 2 ) Y^{L\to H} = Upsample(Conv(X^L,W^{L \to H}),2) YL→H=Upsample(Conv(XL,WL→H),2)
- X L → X L X^L \to X^L XL→XL:从低频到低频,这个部分为直接进行卷积操作 Y L → L = C o n v ( X L , W L → L ) Y^{L \to L} = Conv(X^L,W^{L \to L}) YL→L=Conv(XL,WL→L)
随后考虑高频部分,与低频部分类似有两个部分的操作:
- X H → X H X^H \to X^H XH→XH:从高频到高频,直接进行卷积操作 Y H → H = C o n v ( X H , W H → H ) Y^{H \to H} = Conv(X^H,W^{H \to H}) YH→H=Conv(XH,WH→H)
- X H → X L X^H \to X^L XH→XL:从高频到低频,首先进行stride和kernel均为2的平均值池化,再进行卷积操作,生成与 Y L Y^L YL通道数相同的feature map,最终产生 Y H → L = c o n v ( a v g p o o l ( X H , 2 ) , W H → L ) ) Y^{H \to L} = conv(avgpool(X^H,2),W^{H \to L})) YH→L=conv(avgpool(XH,2),WH→L))
最终,有 Y L = Y H → L + Y L → L Y^L = Y^{H \to L} + Y^{L \to L} YL=YH→L+YL→L和 Y H = Y H → H + Y L → H Y^H = Y^{H \to H} +Y^{L \to H} YH=YH→H+YL→H,因此可以总结如下公式:
Y L = Y H → L + Y L → L = Y H → L = c o n v ( a v g p o o l ( X H , 2 ) , W H → L ) ) + C o n v ( X L , W L → L ) Y H = Y H → H + Y L → H = C o n v ( X H , W H → H ) + U p s a m p l e ( C o n v ( X L , W L → H ) , 2 ) Y^L = Y^{H \to L} + Y^{L \to L} = Y^{H \to L} = conv(avgpool(X^H,2),W^{H \to L})) + Conv(X^L,W^{L \to L}) \\ Y^H = Y^{H \to H} +Y^{L \to H} = Conv(X^H,W^{H \to H}) + Upsample(Conv(X^L,W^{L \to H}),2) YL=YH→L+YL→L=YH→L=conv(avgpool(XH,2),WH→L))+Conv(XL,WL→L)YH=YH→H+YL→H=Conv(XH,WH→H)+Upsample(Conv(XL,WL→H),2)
因此有四个部分的权值:
| 来源/去向 | → H \to H →H | → L \to L →L |
|---|---|---|
| H | W H → H W^{H \to H} WH→H | W H → L W^{H \to L} WH→L |
| L | W L → H W^{L \to H} WL→H | W L → L W^{L \to L} WL→L |
另外进行使用时,在网络的输入和输出需要将两个频率上的Tensor聚合,做法如下:
- 输入部分,取 X = [ X , 0 ] X = [X,0] X=[X,0],即有 X H = X X^H = X XH=X, X L = 0 X^L = 0 XL=0,仅进行 H → L H \to L H→L和 H → H H \to H H→H操作,输出输出的低频仅有X生成,即 Y H = Y H → H Y^H = Y^{H \to H} YH=YH→H和 Y L = Y H → L Y^L = Y^{H \to L} YL=YH→L
- 输出部分,取 X = [ X H , X L ] X = [X^H,X^L] X=[XH,XL], α = 0 \alpha = 0 α=0。即仅进行 L → H L \to H L→H和 H → H H \to H H→H的操作,最终输出为 Y = Y L → H + Y H → H Y = Y^{L \to H} + Y^{H \to H} Y=YL→H+YH→H
性能分析
以下计算均取原Tensor尺寸为 C I × W × H CI \times W \times H CI×W×H,卷积尺寸为 C O × C I × K × K CO \times CI \times K \times K CO×CI×K×K,输出Tensor尺寸为 C O × W × H CO \times W \times H CO×W×H(stride=1,padding设置使feature map尺寸不变)。
计算量分析
Octave卷积的最大优势在于减小计算量,取参数 α \alpha α为低频通道占总通道的比例。首先考虑直接卷积的计算量,对于输出feature map中的每个数据,需要进行 C I × K × K CI \times K \times K CI×K×K次乘加计算,因此总的计算量为:
C c o n v = ( C O × W × H ) × ( C I × K × K ) C_{conv} = (CO \times W \times H) \times (CI \times K \times K) Cconv=(CO×W×H)×(CI×K×K)
现考虑Octave卷积,有四个卷积操作:
- L → L L \to L L→L卷积: C L → L = α 2 × ( C O × W 2 × H 2 ) × ( C I × K × K ) = α 2 4 × C c o n v C_{L \to L} = \alpha^2 \times (CO \times \frac{W}{2} \times \frac{H}{2}) \times (CI \times K \times K) = \frac{\alpha^2}{4} \times C_{conv} CL→L=α2×(CO×2W×2H)×(CI×K×K)=4α2×Cconv
- L → H L \to H L→H卷积: C L → H = ( ( 1 − α ) × C O × W 2 × H 2 ) × ( α × C I × K × K ) = α ( 1 − α ) 4 × C c o n v C_{L \to H} = ((1 - \alpha) \times CO \times \frac{W}{2} \times \frac{H}{2}) \times ( \alpha \times CI \times K \times K) = \frac{\alpha(1-\alpha)}{4} \times C_{conv} CL→H=((1−α)×CO×2W×2H)×(α×CI×K×K)=4α(1−α)×Cconv
- H → L H \to L H→L卷积: C H → L = ( α × C O × W 2 × H 2 ) × ( ( 1 − α ) × C I × K × K ) = α ( 1 − α ) 4 × C c o n v C_{H \to L} = (\alpha \times CO \times \frac{W}{2} \times \frac{H}{2}) \times ((1 - \alpha) \times CI \times K \times K) = \frac{\alpha(1-\alpha)}{4} \times C_{conv} CH→L=(α×CO×2W×2H)×((1−α)×CI×K×K)=4α(1−α)×Cconv
- H → H H \to H H→H卷积: C H → H = ( ( 1 − α ) × C O × W × H ) × ( ( 1 − α ) × C I × K × K ) = ( 1 − α ) 2 × C c o n v C_{H \to H} = ((1 - \alpha) \times CO \times W \times H) \times ((1 - \alpha) \times CI \times K \times K) = (1 - \alpha)^2 \times C_{conv} CH→H=((1−α)×CO×W×H)×((1−α)×CI×K×K)=(1−α)2×Cconv
总上,可以得出计算量有:
C o c t a v e C c o n v = α 2 + 2 α ( 1 − α ) + 4 ( 1 − α ) 2 4 = 1 − 3 4 α ( 2 − α ) \frac{C_{octave}}{C_{conv}} = \frac{\alpha^2 + 2\alpha(1-\alpha) + 4 (1 - \alpha)^2}{4} = 1 - \frac{3}{4}\alpha(2- \alpha) CconvCoctave=4α2+2α(1−α)+4(1−α)2=1−43α(2−α)
在 α ∈ [ 0 , 1 ] \alpha \in [0,1] α∈[0,1]中单调递减,当取 α = 1 \alpha = 1 α=1时,有 C o c t a v e C c o n v = 1 4 \frac{C_{octave}}{C_{conv}} = \frac{1}{4} CconvCoctave=41。
参数量分析
原卷积的参数量为:
W c o n v = C O × C I × K × K W_{conv} = CO \times CI \times K \times K Wconv=CO×CI×K×K
Octave卷积将该部分分为四个,对于每个卷积有:
- L → L L \to L L→L卷积: W L → L = ( α × C O ) × ( α × C I ) × K × K = α 2 × W c o n v W_{L \to L} =(\alpha\times CO) \times (\alpha \times CI) \times K \times K = \alpha^2 \times W_{conv} WL→L=(α×CO)×(α×CI)×K×K=α2×Wconv
- L → H L \to H L→H卷积: W L → H = ( ( 1 − α ) × C O ) × ( α × C I ) × K × K = α ( 1 − α ) × W c o n v W_{L \to H} =((1-\alpha) \times CO) \times (\alpha \times CI) \times K \times K = \alpha(1 - \alpha) \times W_{conv} WL→H=((1−α)×CO)×(α×CI)×K×K=α(1−α)×Wconv
- H → L H \to L H→L卷积: W H → L = ( α × C O ) × ( ( 1 − α ) × C I ) × K × K = α ( 1 − α ) × W c o n v W_{H \to L} =(\alpha \times CO) \times ((1-\alpha) \times CI) \times K \times K = \alpha(1 - \alpha) \times W_{conv} WH→L=(α×CO)×((1−α)×CI)×K×K=α(1−α)×Wconv
- H → H H \to H H→H卷积: W H → L = ( ( 1 − α ) × C O ) × ( ( 1 − α ) × C I ) × K × K = ( 1 − α ) 2 × W c o n v W_{H \to L} =((1-\alpha) \times CO) \times ((1-\alpha) \times CI) \times K \times K = (1 - \alpha)^2 \times W_{conv} WH→L=((1−α)×CO)×((1−α)×CI)×K×K=(1−α)2×Wconv
因此共有参数量:
C o c t a v e = ( α 2 + 2 α ( 1 − α ) + ( 1 − α ) 2 ) × C c o n v = C c o n v C_{octave} = (\alpha^2 + 2\alpha(1 - \alpha) + (1 - \alpha)^2) \times C_{conv} = C_{conv} Coctave=(α2+2α(1−α)+(1−α)2)×Cconv=Cconv
由此,参数量没有发生变化,该方法无法减少参数量。
Octave卷积实现
Octave卷积模块
以下实现了一个兼容普通卷积的Octave卷积模块,针对不同的高频低频feature map的通道数,分为以下几种情况:
Lout_channel != 0 and Lin_channel != 0:通用Octave卷积,需要四个卷积参数Lout_channel == 0 and Lin_channel != 0:输出Octave卷积,输入有低频部分,输出无低频部分,仅需要两个卷积参数Lout_channel != 0 and Lin_channel == 0:输入Octave卷积,输入无低频部分,输出有低频部分,仅需要两个卷积参数Lout_channel == 0 and Lin_channel == 0:退化为普通卷积,输入输出均无低频部分,仅有一个卷积参数
class OctaveConv(pt.nn.Module):
def __init__(self,Lin_channel,Hin_channel,Lout_channel,Hout_channel,
kernel,stride,padding):
super(OctaveConv, self).__init__()
if Lout_channel != 0 and Lin_channel != 0:
self.convL2L = pt.nn.Conv2d(Lin_channel,Lout_channel, kernel,stride,padding)
self.convH2L = pt.nn.Conv2d(Hin_channel,Lout_channel, kernel,stride,padding)
self.convL2H = pt.nn.Conv2d(Lin_channel,Hout_channel, kernel,stride,padding)
self.convH2H = pt.nn.Conv2d(Hin_channel,Hout_channel, kernel,stride,padding)
elif Lout_channel == 0 and Lin_channel != 0:
self.convL2L = None
self.convH2L = None
self.convL2H = pt.nn.Conv2d(Lin_channel,Hout_channel, kernel,stride,padding)
self.convH2H = pt.nn.Conv2d(Hin_channel,Hout_channel, kernel,stride,padding)
elif Lout_channel != 0 and Lin_channel == 0:
self.convL2L = None
self.convH2L = pt.nn.Conv2d(Hin_channel,Lout_channel, kernel,stride,padding)
self.convL2H = None
self.convH2H = pt.nn.Conv2d(Hin_channel,Hout_channel, kernel,stride,padding)
else:
self.convL2L = None
self.convH2L = None
self.convL2H = None
self.convH2H = pt.nn.Conv2d(Hin_channel,Hout_channel, kernel,stride,padding)
self.upsample = pt.nn.Upsample(scale_factor=2)
self.pool = pt.nn.AvgPool2d(2)
def forward(self,Lx,Hx):
if self.convL2L is not None:
L2Ly = self.convL2L(Lx)
else:
L2Ly = 0
if self.convL2H is not None:
L2Hy = self.upsample(self.convL2H(Lx))
else:
L2Hy = 0
if self.convH2L is not None:
H2Ly = self.convH2L(self.pool(Hx))
else:
H2Ly = 0
if self.convH2H is not None:
H2Hy = self.convH2H(Hx)
else:
H2Hy = 0
return L2Ly+H2Ly,L2Hy+H2Hy
在前项传播的过程中,根据是否有对应的卷积操作参数判断是否进行卷积,若不进行卷积,将输出置为0。前向传播时,输入为低频和高频两个feature map,输出为低频和高频两个feature map,输入情况和参数配置应与通道数的配置匹配。
其他部分
使用MNIST数据集,构建了一个三层卷积+两层全连接层的神经网络,使用Adam优化器训练,代价函数使用交叉熵函数,训练3轮,最后在测试集上进行测试。
import torch as pt
import torchvision as ptv
# download dataset
train_dataset = ptv.datasets.MNIST("./",train=True,download=True,transform=ptv.transforms.ToTensor())
test_dataset = ptv.datasets.MNIST("./",train=False,download=True,transform=ptv.transforms.ToTensor())
train_loader = pt.utils.data.DataLoader(train_dataset,batch_size=64,shuffle=True)
test_loader = pt.utils.data.DataLoader(test_dataset,batch_size=64,shuffle=True)
# build network
class mnist_model(pt.nn.Module):
def __init__(self):
super(mnist_model, self).__init__()
self.conv1 = OctaveConv(0,1,8,8,kernel=3,stride=1,padding=1)
self.conv2 = OctaveConv(8,8,16,16,kernel=3,stride=1,padding=1)
self.conv3 = OctaveConv(16,16,0,64,kernel=3,stride=1,padding=1)
self.pool = pt.nn.MaxPool2d(2)
self.relu = pt.nn.ReLU()
self.fc1 = pt.nn.Linear(64*7*7,256)
self.fc2 = pt.nn.Linear(256,10)
def forward(self,x):
out = [self.pool(self.relu(i)) for i in self.conv1(0,x)]
out = self.conv2(*out)
_,out = self.conv3(*out)
out = self.fc1(self.pool(self.relu(out)).view(-1,64*7*7))
return self.fc2(out)
net = mnist_model().cuda()
# print(net)
# prepare training
def acc(outputs,label):
_,data = pt.max(outputs,dim=1)
return pt.mean((data.float()==label.float()).float()).item()
lossfunc = pt.nn.CrossEntropyLoss().cuda()
optimizer = pt.optim.Adam(net.parameters())
# train
for _ in range(3):
for i,(data,label) in enumerate(train_loader) :
optimizer.zero_grad()
# print(i,data,label)
data,label = data.cuda(),label.cuda()
outputs = net(data)
loss = lossfunc(outputs,label)
loss.backward()
optimizer.step()
if i % 100 == 0:
print(i,loss.cpu().data.item(),acc(outputs,label))
# test
acc_list = []
for i,(data,label) in enumerate(test_loader):
data,label = data.cuda(),label.cuda()
outputs = net(data)
acc_list.append(acc(outputs,label))
print("Test:",sum(acc_list)/len(acc_list))
# save
pt.save(net,"./model.pth")
最终获得模型的准确率为0.988