吴恩达ex3手写数字识别（逻辑回归+神经网络）python实现

手写数字识别python实现（逻辑回归+神经网络）

import numpy as np
import matplotlib.pyplot as plt
import os
import random
import time
import pandas as pd
import scipy.io as io
import scipy.optimize as opt

handw = io.loadmat('ex3data1.mat')
handw_X = handw['X']
handw_y = handw['y']

1.Visualizing the data

def displayData(data):
    m, n = data.shape
    random_num = random.sample(range(m), 100)
    X = data[random_num]
    plt.figure(figsize=(8,8))
    for i in range(X.shape[0]):
        ax = plt.subplot(10,10,i+1)
        ax.imshow(X[i].reshape(20,20))
        plt.axis('off')
        plt.margins(0,0)
    plt.show()

2.One-vs-all Classification

#LR
def sigmoid_function(z):
    re_z = 1/(1+np.exp(-z))
    return re_z

# nums = np.arange(-10,10,step=1)
# fig,ax = plt.subplots(figsize=(6,4))
# ax.plot(nums, sigmoid_function(nums), 'r')
# plt.show()

def model(x, theta):
    return sigmoid_function(x.dot(theta))

def cost_function(theta,X, y):
    el = 1e-5
    h = model(X, theta)
    cost = -y * np.log(h+el) - (1-y)*np.log(1-h+el)
    return cost.sum()/X.shape[0]


def gradient(theta,X, y):
    m, n = X.shape
    h = model(X, theta)
    grad = (1/m) * (X.T @ (h-y))
    return grad

def decision_boundary(x1, theta):
    theta = theta.reshape(-1,1)
    x2 = -theta[0]-theta[1]*x1
    return x2/theta[2]

def onevsall(theta, X, y):
    m, n = X.shape
    K = 10
    theta_new = np.zeros((K,n))
    for i in range(K):
        yi = []
        for item in y.flatten():
            if item == i+1:
                yi.append(1)
            else:
                yi.append(0)
        yi = np.array(yi)
        result_opt = opt.fmin_tnc(func=cost_function, x0=theta.flatten(), fprime=gradient, args=(X,yi.flatten()))
        theta_new[i] = result_opt[0]
    
    return theta_new

X = np.c_[np.ones((5000,1)),handw_X]
y = handw_y
theta = np.zeros((401,1))
result = onevsall(theta,X, y)

2.1 One-vs-all Prediction

def onevsall_prediction(theta, X):
    m, n = X.shape
    pre = []
    for i in range(m):
        pre_num = sigmoid_function(X[i] @ theta.T)
        pre_num2 = np.where(pre_num == pre_num.max())[0]
        pre.append(pre_num2+1)
    pre = np.array(pre)
    return pre 

p = onevsall_prediction(result,X)

acc_num = 0
for i in range(5000):
    if p[i] == y[i]:
        acc_num += 1
acc_num/5000#0.9918

3.Neural Networks

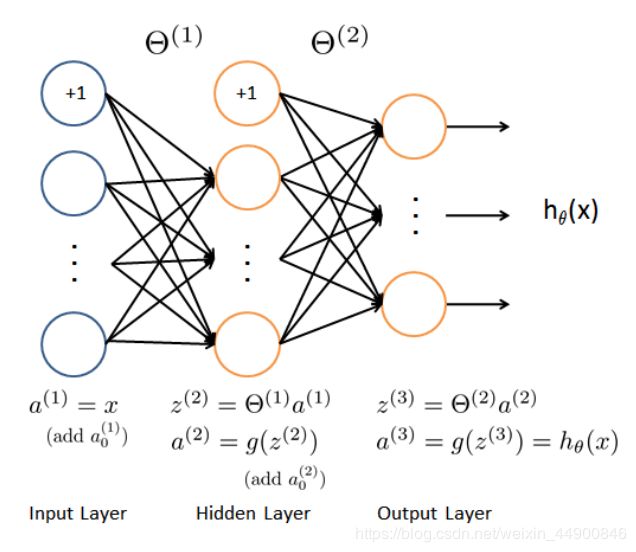
theta_trained = io.loadmat('ex3weights.mat')

theta_train1 = theta_trained['Theta1']
theta_train2 = theta_trained['Theta2']
theta_train1.shape, theta_train2.shape

3.1Feedforward Propagation and Prediction

def feed_nn(X, theta_train1, theta_train2):
    m,n = X.shape
    bias = np.ones((1,m))
    a2 = sigmoid_function(theta_train1 @ X.T)
    a2_bias = np.r_[bias, a2]
    a3 = sigmoid_function(theta_train2 @ a2_bias)
    pre_array = []
    for i in range(m):
        xi = a3[:,i]
        max_num = np.where(xi==xi.max())[0]
        pre_array.append(max_num+1)
    pre_array = np.array(pre_array)
    return pre_array

y_pre = feed_nn(X, theta_train1, theta_train2)

acc_num2 = 0
for i in range(5000):
    if y_pre[i] == y[i]:
        acc_num2 += 1
acc_num2/5000#0.9752