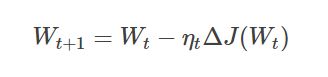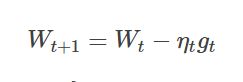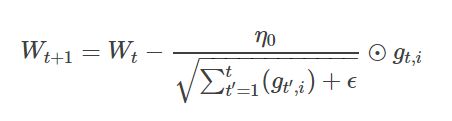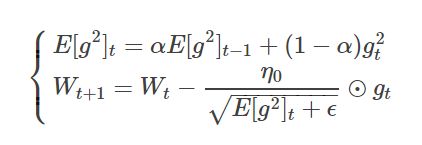各种优化器Optimizer原理：从SGD到AdamOptimizer
各种优化器Optimizer原理：从SGD到AdamOptimizer
- （一）优化器Optimizer综述：
- （二）基本梯度下降法
- 2.0 核心思想：
- 2.1 标准梯度下降法（GD，Gradient Descent）
- 2.1.1 数学公式：
- 2.1.2 优缺点：
- 2.2 批量梯度下降法（BGD, Batch Gradient Descent）
- 2.2.1 数学公式：
- 2.2.2 优缺点：
- 2.3 随机梯度下降法（SGD，Stochastic Gradient Descent）
- 2.3.1 数学公式：
- 2.3.2 优缺点：
- （三）动量优化法
- 3.0 核心思想：
- 3.1 标准动量优化方法（MomentumOptimizer)
- 3.1.1 数学公式：
- 3.1.2 优缺点：
- 3.2 牛顿加速梯度动量优化方法(NAG, Nesterov accelerated gradient)
- 3.2.1 数学公式：
- 3.2.2 优缺点：
- （四）自适应学习率优化算法
- 4.0 核心思想：
- 4.1 Adam算法（Adaptive moment estimation）
- 4.1.1 数学公式：
- 4.1.2 优缺点：
- 4.2 AdaGrad算法（Adaptive Gradient Algorithm）
- 4.2.1 数学公式：
- 4.2.3 优缺点：
- 4.3 RMSProp算法
- 4.3.1 数学公式：
- 4.3.2 优缺点：
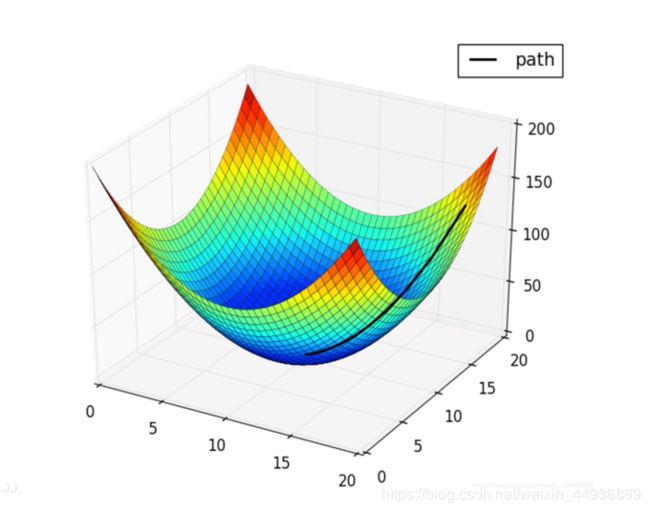
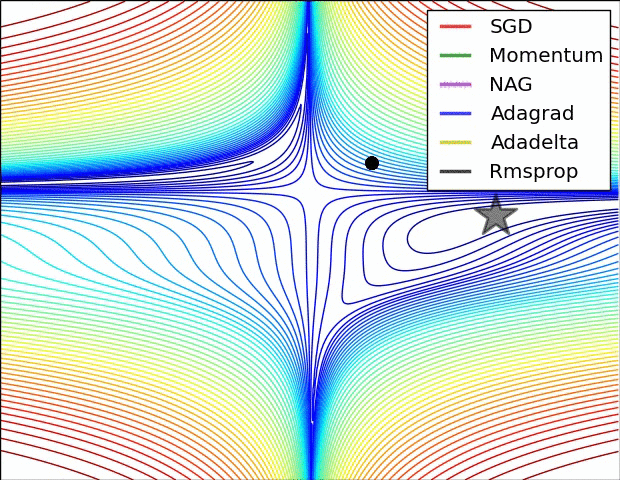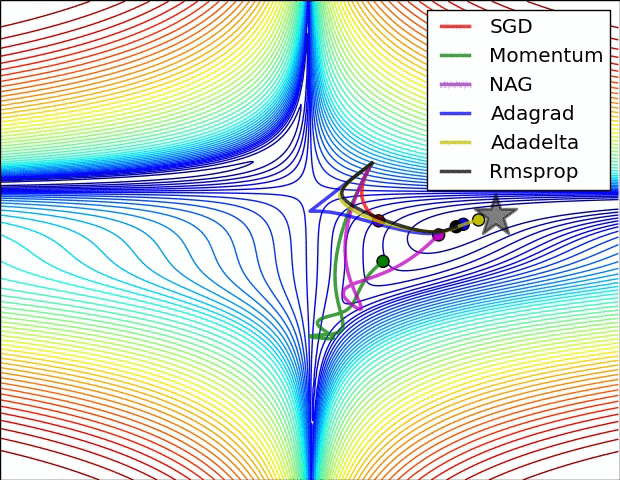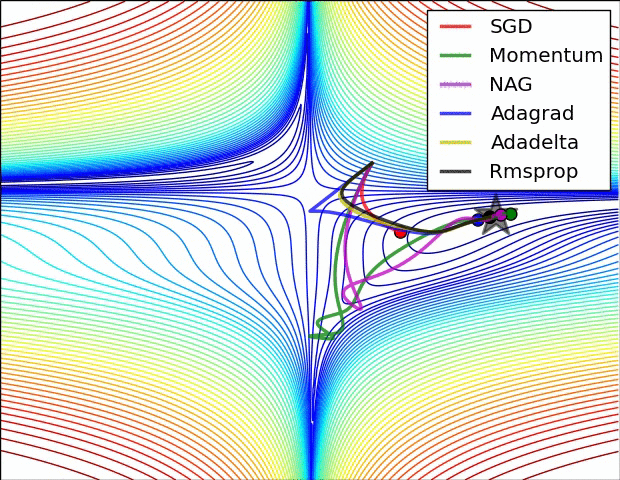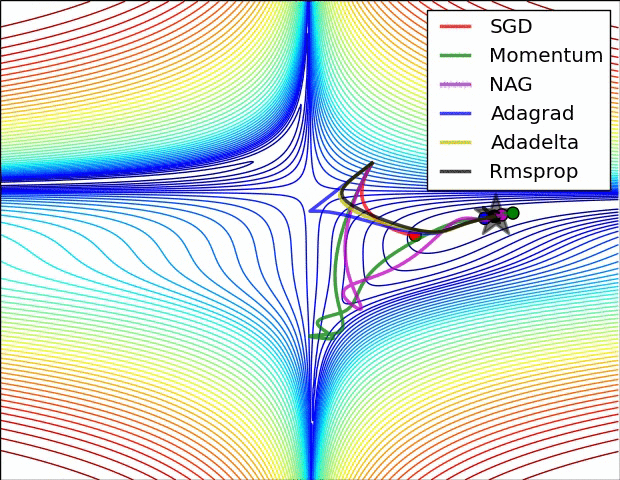
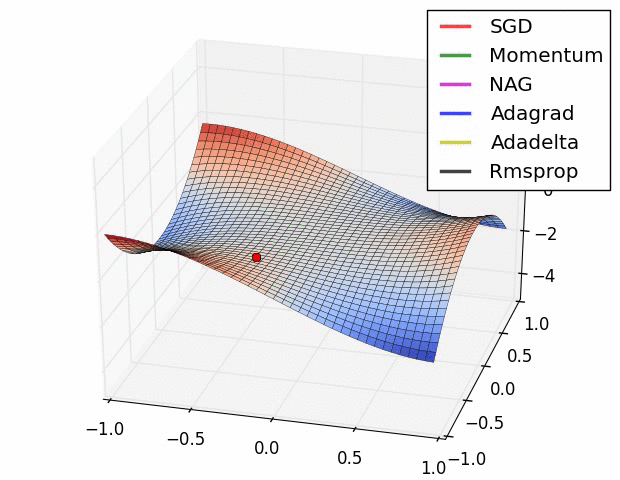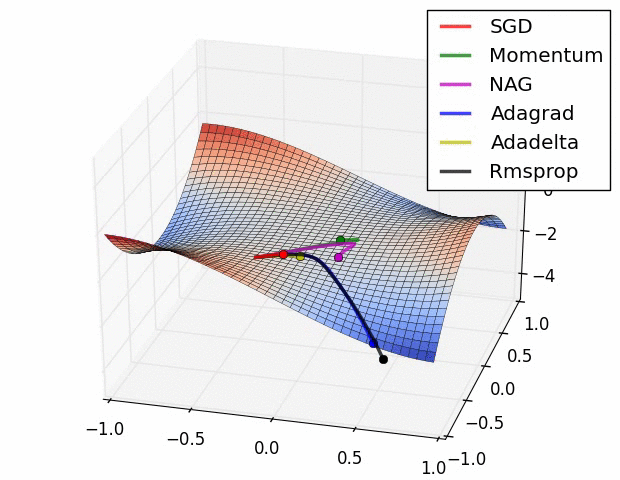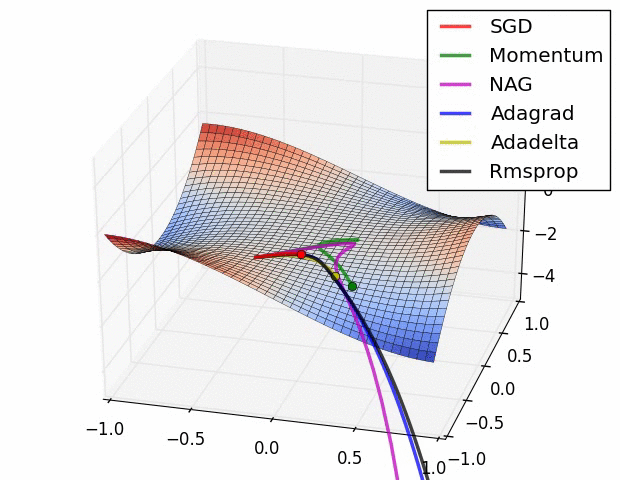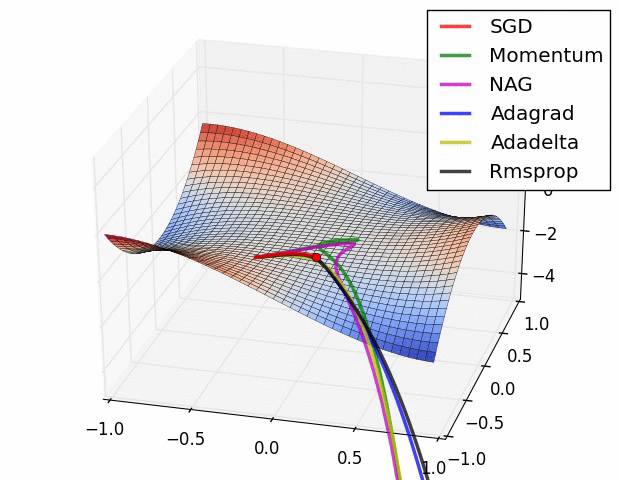
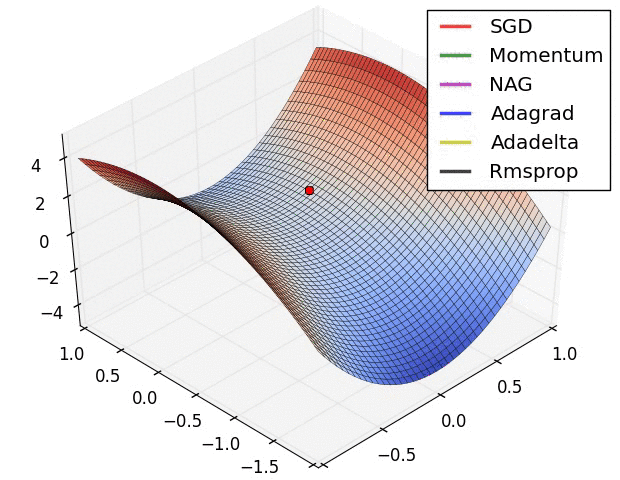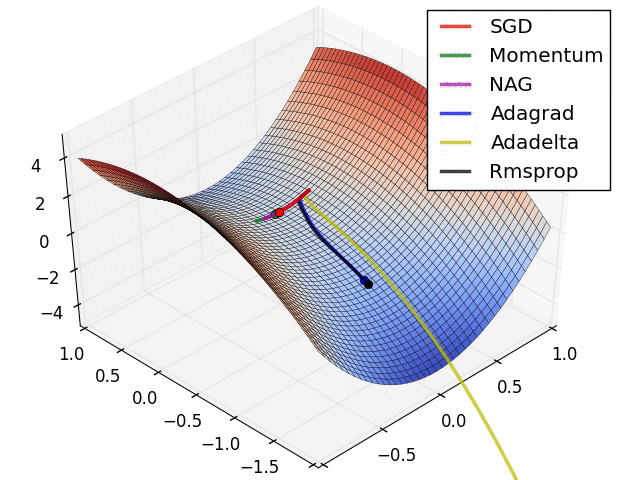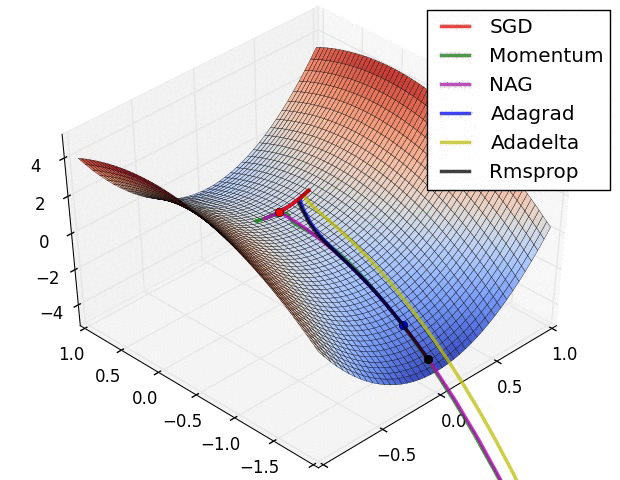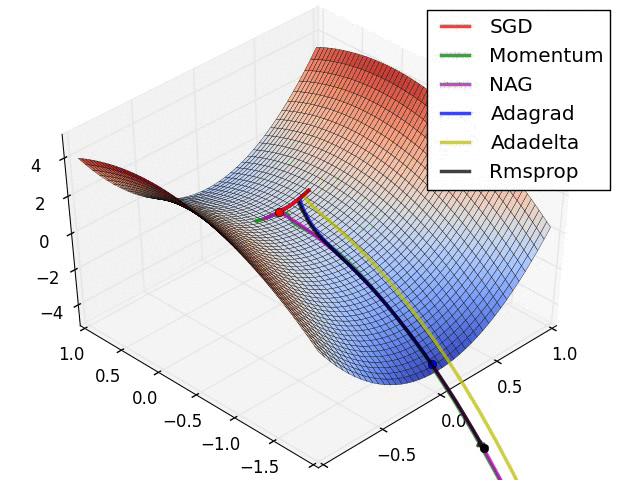
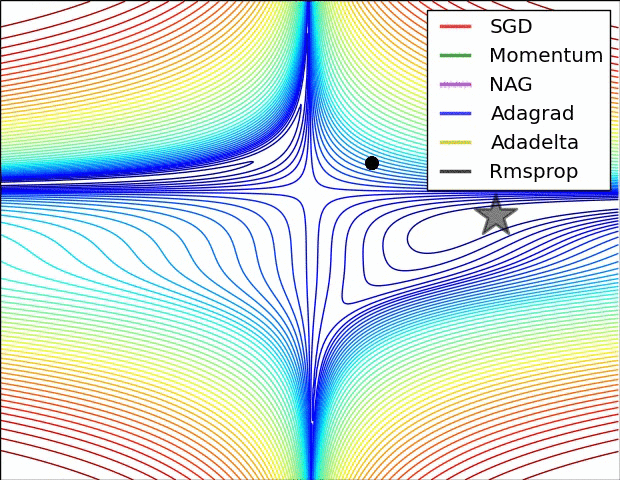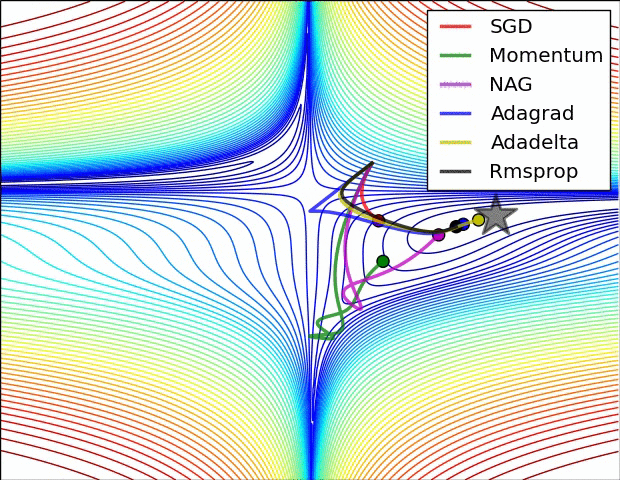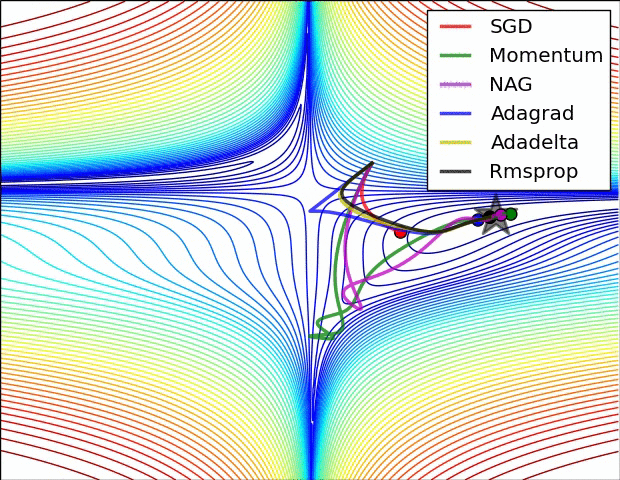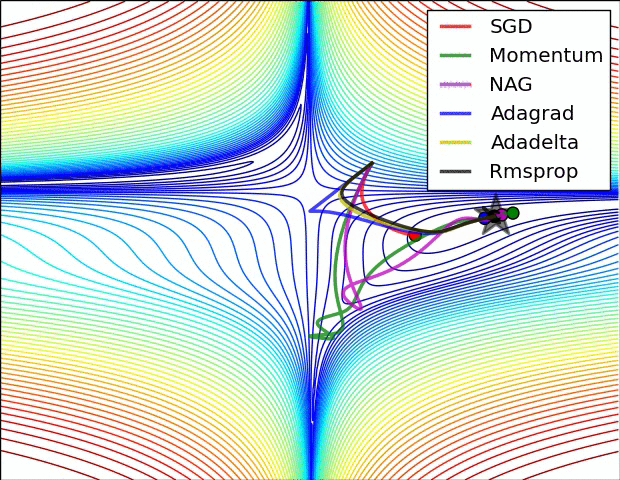
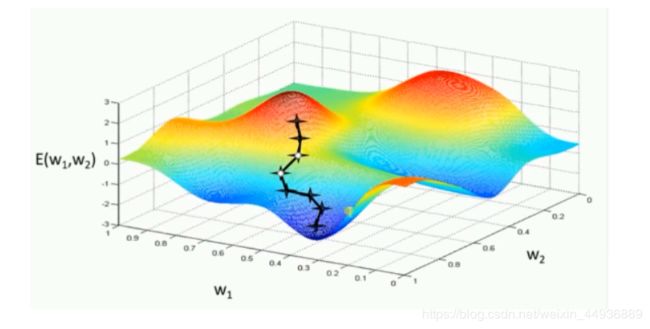
- （五）各种优化器的可视化比较：
- （示例一）
- （示例二）
- （示例三）
（一）优化器Optimizer综述：
优化器是神经网络训练过程中，进行梯度下降以寻找最优解的优化方法。不同方法通过不同方式（如附加动量项，学习率自适应变化等）侧重于解决不同的问题，但最终大都是为了加快训练速度。
对于这些优化器，有一张图能够最直接地表现它们的性能：
这里就介绍几种常见的优化器，包括其原理、数学公式、核心思想及其性能；
这些优化器可分为三大类：
- 基本梯度下降法，包括标准梯度下降法(GD, Gradient Descent)，随机梯度下降法(SGD, Stochastic Gradient Descent)及批量梯度下降法(BGD, Batch Gradient Descent)；
- 动量优化法，包括标准动量优化方法（MomentumOptimizer)、牛顿加速梯度动量优化方法(NAG, Nesterov accelerated gradient)等；
- 自适应学习率优化算法，包括AdaGrad算法，RMSProp算法，Adam算法等；
（二）基本梯度下降法
2.0 核心思想：
即针对每次输入的训练数据，计算输出预测与真值的Loss的梯度；
2.1 标准梯度下降法（GD，Gradient Descent）
2.1.1 数学公式：
参数解析：
- 其中 Wt 表示当前时刻网络中的变量（包括权重weights、偏置biases和卷积核等），即参与梯度下降的变量；Wt+1 表示更新后的变量；
- ηt 表示学习率；
- J是损失函数（即所有样本X的预测值与真实值的Loss），则 ΔJ(Wt) 表示损失函数 J 对 Wt 中的变量的偏导；
从表达式来看，网络中参数的更新，是不断向着最小化Loss函数的方向移动的：
2.1.2 优缺点：
标准梯度下降法（Gradient Descent）最大的优点就是简单易懂，即对于相应的最优解（这里认为是Loss的最小函数），每次变量更新都是沿着局部梯度下降最快的方向，从而最小化损失函数。
缺点就是：
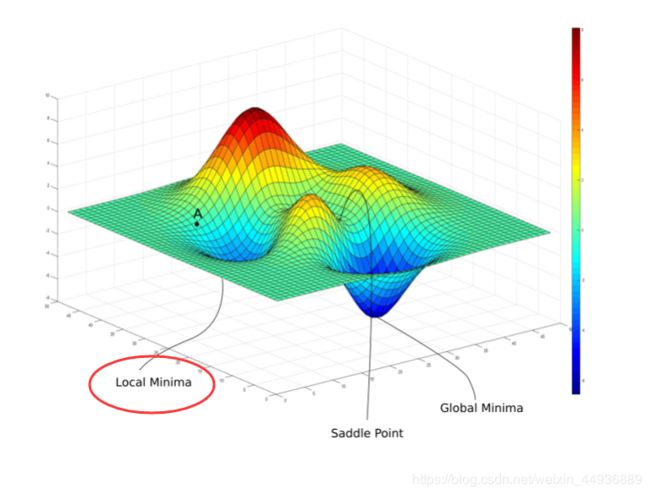
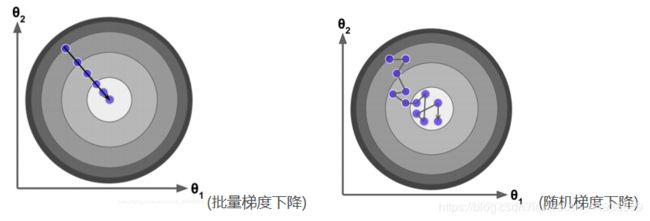
- 如上图所示，局部梯度下降最大的方向，并非一定是最优解的方向，并且每次训练都要遍历所有样本，导致训练速度较慢；
- 容易陷入局部最优点，即落入鞍点；此时每次计算时，梯度都为0或者是一个很小的数，导致被困在局部最优点，而不能到达全局最优点；
- 注意有的文章认为，由于输入变量的维度一般较高，很少存在或者说很少能够陷入每一维都是局部最优点构成的鞍点，因此这里存疑；
2.2 批量梯度下降法（BGD, Batch Gradient Descent）
2.2.1 数学公式：
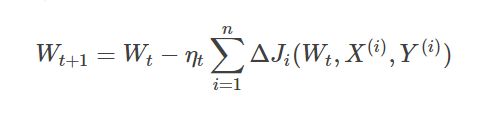
不同于标准梯度下降法（Gradient Descent）一次计算所有数据样本的Loss并计算相应的梯度，批量梯度下降法（BGD, Batch Gradient Descent）每次只取一个小批次的数据及其真实标签进行训练，称这个批次为mini-batch；
其中：
- X(i),Y(i) 是一个mini-batch 的输入数据和真实标签；
- ΔJ(Wt) 是这个 mini-batch 的数据的Loss；
2.2.2 优缺点：
缺点是随机梯度下降法的 batch size 选择不当可能导致模型难以收敛；
优点是：
- 每次使用一个batch可以大大减小收敛所需要的迭代次数，同时可以使收敛到的结果更加接近梯度下降的效果。
- 由于矩阵的并行计算，训练速度并不会比每次训练单个样本慢；
- 加快模型收敛速度；
2.3 随机梯度下降法（SGD，Stochastic Gradient Descent）
2.3.1 数学公式：
其中 gt 是单个样本对权重等参数的偏导；
即训练时，每次只从一批训练样本中随机选取一个样本进行梯度下降；对随机梯度下降来说，只需要一次关注一个训练样本，一点点把参数朝着全局最小值的方向进行修改了。
2.3.2 优缺点：
缺点是：
- 梯度下降速度比较慢，而且每次梯度更新时往往只专注与局部最优点，而不会恰好指向全局最优点；
- 单样本梯度更新时会引入许多噪声（跟训练目标无关的特征也会被归为该样本分类的特征）；
优点是：
当处理大量数据时，比如SSD或者faster-rcnn等目标检测模型，每个样本都有大量候选框参与训练，这时使用随机梯度下降法能够加快梯度的计算。
（三）动量优化法
3.0 核心思想：
动量优化方法是在梯度下降法的基础上进行的改变，具有加速梯度下降的作用；
其核心思想就是，使当前训练数据的梯度受到之前训练数据的梯度的影响，其中之前的梯度乘上一个权重值λ（λ<1），就成为动量项（注意这里把梯度看作了有方向的向量）。而且随着迭代次数的增加，越往前的梯度对当前梯度的影响就越小。
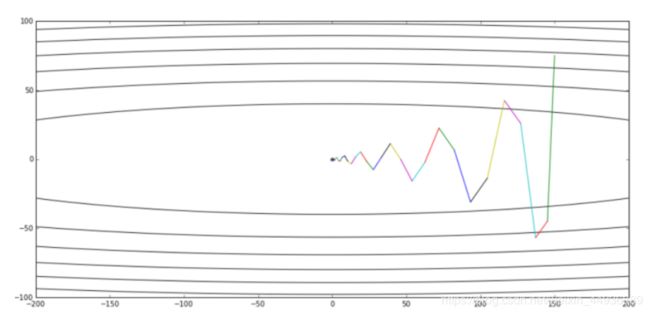
不使用动量优化时，每次训练的梯度下降方向，都是按照当前批次训练数据计算的，可能并不能代表整个数据集，并且会有许多噪声，下降曲线波动较大：
添加动量项之后，能够有效减小波动，从而加快训练速度：
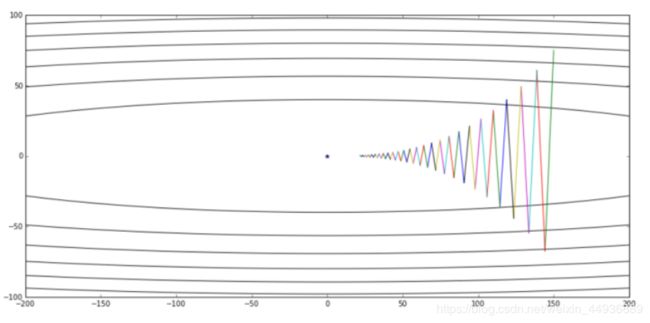
3.1 标准动量优化方法（MomentumOptimizer)
3.1.1 数学公式：
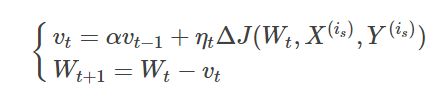
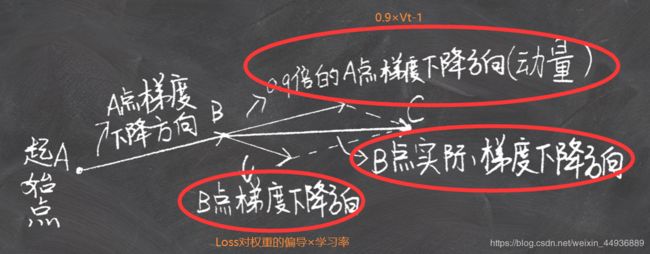
Vt 的计算如图，是上一次训值练的 Vt-1 × 衰减率α + 学习率η × 损失函数的偏导；
其中 Vt 是 t 时刻权重更新的值，即 Wt+1 = Wt - Vt；衰减率α通常取0.9；
用向量图表示为：
3.1.2 优缺点：
优点：
- 通过动量更新，参数向量会在有持续梯度的方向上增加速度；
- 使梯度下降时的折返情况减轻，从而加快训练速度；
缺点：
如果数据集分类复杂，会导致 Vt-1 和 t时刻梯度 向量方向相差较大；在进行向量求和时，得到的 Vt 会非常小，反而使训练速度大大下降甚至模型难以收敛。
3.2 牛顿加速梯度动量优化方法(NAG, Nesterov accelerated gradient)
3.2.1 数学公式：
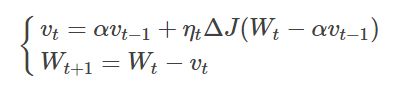
这里与Momentum梯度动量优化法不同的是，在计算参数梯度之前，会超前一个动量单位，即图中计算的是损失函数对 Wt - α×Vt-1的偏导，相当于对于Momentum多了一个本次梯度相对上次梯度的变化量。
3.2.2 优缺点：
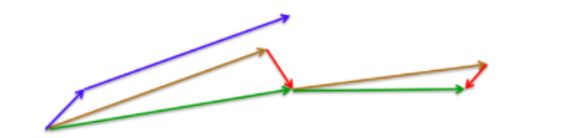
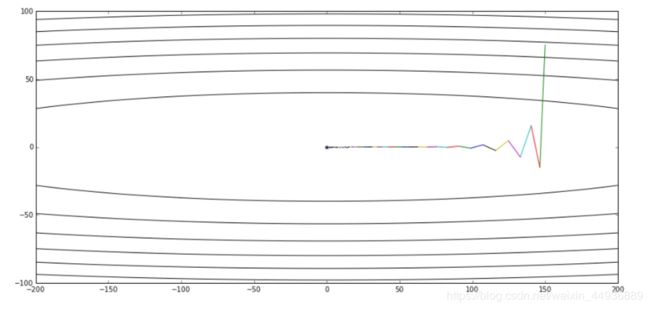
如图，蓝色的是Momentum梯度动量优化法的下降方向，即如果多次梯度累计方向大致相同，会导致最终下降步幅过大；
故NAG可以有效利用损失函数的近似二阶导，从而加快收敛速度。
更详细的解读看这里：知乎《比Momentum更快：揭开Nesterov Accelerated Gradient的真面目》
（四）自适应学习率优化算法
4.0 核心思想：
自适应学习率优化算法针对于机器学习模型的学习率，采用不同的策略来调整训练过程中的学习率，从而大大提高训练速度。
4.1 Adam算法（Adaptive moment estimation）
4.1.1 数学公式：
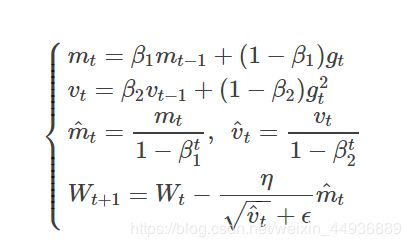
其中，mt和vt分别为一阶动量项和二阶动量项。β1,β2为动力值大小（通常分别取0.9和0.999）；
m^ t，v^ t分别为各自的修正值。Wt表示t时刻即第t迭代模型的参数;
gt表示t次迭代代价函数关于WW的梯度大小；
ϵ是一个取值很小的数（一般为1e-8，为了避免分母为0）；
4.1.2 优缺点：
优点：
- 计算高效；
- 梯度平滑、稳定的过渡，可以适应不稳定的目标函数；
- 调参相对简单，默认参数就可以处理绝大部分的问题
4.2 AdaGrad算法（Adaptive Gradient Algorithm）
4.2.1 数学公式：
AdaGrad的核心思想是，缩放每个参数反比于其所有梯度历史平均值总和的平方根。具有代价函数最大梯度的参数相应地有较大的学习率，而具有小梯度的参数又较小的学习率。
式中，i表示第i个分类，t表示第t迭代同时也表示分类i累计出现的次数。η0表示初始的学习率取值（一般为0.01）。
4.2.3 优缺点：
优点是：
- AdaGrad算法能够随着训练过程自动减小学习率；
- 对于分布稀疏或者不均衡的数据集，AdaGrad算法在学习率上有很好的适应性；
缺点是：
随着迭代次数增多，学习率会越来越小，最终会趋近于0；
4.3 RMSProp算法
4.3.1 数学公式：
RMSProp算法修改了AdaGrad的梯度积累为指数加权的移动平均。
如图，E[g2]t 表示前 t 次的梯度平方的均值，其余参数跟上面的类似。
4.3.2 优缺点：
优点：
由于取了个加权平均，避免了学习率越来越低的的问题，而且能自适应地调节学习率。
（五）各种优化器的可视化比较：
（示例一）
（示例二）
（示例三）
