Hopfield神经网络实验详解（MATLAB实现）

前言

分享第二弹，一份神经网络课上布置的实验报告。参数什么的可能在不同电脑上需要有所调整，还望用餐愉快。在此之前会简要介绍一下Hopfield神经网络的知识点。

Hopfield网络（离散型）

Hopfield网络属于一种经典的递归神经网络。此外，Hopfield网络还分为离散型和连续型两种。连续型hopfield网络可以根据权值调整连接计算机硬件优化电路计算，当时还提出了一个非常诱人的研究：神经网络计算机。而我们主要介绍的是离散型hopfield网络。

方程描述

学习规则

文字描述：当神经元输入与输出节点的状态相同（即同时兴奋或抑制）时，从第j个到第i个神经元之间的连接强度则增强，否则则减弱。

公式描述：$w_{ij}=\alpha {\sum }_{\genfrac{}{}{0ex}{}{k=1}{i\ne j}}^q{t}_j^k{t}_i^k$，其中$\alpha$为系数。

状态轨迹

渐近稳定点：$t\to \infty$时从初始状态收敛的点。又称为吸引子，对应的稳定域称为吸引域。

不稳定平衡点：在某些特定的轨迹演化过程中，能够到达的稳定点，但对于其它方向上的任意一个小的区域，其轨迹在时间t以后总是偏离 。

伪稳定点：网络最终稳定到一个渐近稳定点上，但这个稳定点不是网络设计所要求的解，这个稳定点为伪稳定点。

霍普菲尔德网络利用稳定吸引子来对信息进行储存，利用从初始状态到稳定吸引子的运行过程来实现对信息的联想存取。

平衡点与输入节点、记忆关系的讨论

输入为两个节点

当记忆平衡点数为2时，网络将整个平面以两个平衡点连线的垂直平分线为分界线划分为两个稳定域。输入除了收敛到两个稳定点外，垂直平分线上的点还会收敛到垂直平分线与连线交点（多数为原点）这个不稳定平衡点上。

当记忆平衡点数为3时，稳定域变为3个四分之一平面。输入除了可能收敛到不稳定平衡点外，还会收敛到一个伪稳定点。

当记忆平衡点数为4时，稳定域为4个四分之一平面。会收敛到不稳定平衡点。

输入为三个节点

当网络只记忆两个平衡点时，其收敛域应为以两点连线的垂直平分面为分界面的两点所在的空间，垂直平分面上的点均收敛到对应的含有0的坐标点上，这些坐标点均是不稳定的平衡点。

当网络记忆三个平衡点时，其收敛域为由三个点所组成的三角形平面上，从每条边上垂直截下的平面所组成的三个子空间。同样，三个垂直平面上的点均收敛到某个含0的坐标点上，这些坐标点均为不稳定的平衡点。

当网络记忆四个以及多于四个平衡点时，其收敛域为空间上的八个象限，且有未被记忆的平衡点，在网络运行工作时，可能会以伪稳定点的形式出现。正交化设计方法的另一个优点则是使网络工作时，尽量少地出现伪稳定点。

输入为r个节点

对于具有r个输入神经元、输出函数为 ±1的反馈网络，当采用正交权值设计法，所设计的网络最多具有 3^r个平衡点，其中，2^r个是稳定的平衡点，另外 3^r-2^r个是不稳定的平衡点。每个稳定点的稳定域（吸引域）为以该点为中心，棱长为2的多边体（形），各平衡域的边界部分为不稳定平衡点的吸引域，不稳定的平衡点在两两稳定平衡点连线的中点上。

题目

试设计一个反馈网络存储下列目标平衡点：T= [ 1 -1; -1 1 ]; 并用6组任意随机初始列矢量，包括一组在目标平衡点连线的垂直平分线上的一点作为输入矢量对所设计的网络的平衡点进行测试，观察3次循环的每一次的输出结果。给出最后收敛到各自平衡点（或不稳定的平衡点）结果的次数。

解答

1. 网络结构设计

利用MATLAB的神经网络工具箱可以轻松设计出该霍普菲尔德网络：

clear;
T = [1 -1;-1 1];                                            %存储目标平衡点
net = newhop(T);                                       	 %建立霍普菲尔德网络
W = net.lw{1,1};                                   %读取网络返回的权值与偏差
b = net.b{1};
Ptest = [1 -1;-1 1];                                  %输入目标矢量用作测试
[Y1,Pf1,Af1] = sim(net,{2,3},[],Ptest);          %计算其网络循环结束后的输出
A1 = Y1{1}; A2 = Y1{2};A3 = Y1{3};                      %给出三次循环的结果

其中，我们将目标平衡点作为输入对网络进行测试，循环三次测试，最后得到的结果均为[1 -1;-1 1]，即第一次循环后就已经达到了目标。

2. 实验结果

根据要求，6组矢量中要求其中一组为目标平衡点连线的垂直平分线上的一点，即在y=x直线上的任意一点即可。然后将向量输入到网络中进行循环，并绘制图像为：

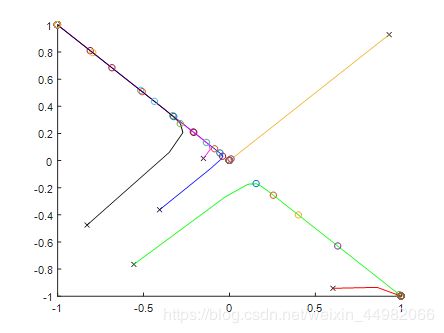
它们最后收敛到各自平衡点的次数分别为：
16 26 17 12 2 5
其中，有两个点收敛到[1;-1]，有三个点收敛到[-1;1]，而垂直平分线上的点收敛到了[0;0]，这是一个不稳定的平衡点。在本人电脑的记录中，每次循环后改点的数值都在不断变化，甚至已经到了10^-40的量级，无限逼近于原点。