阿尔法python 第五章 函数和代码复用
函数和代码复用
- 打招呼函数
- 能否组成三角形
- 计算n个自然数的立方和
- 简单计算器实现
- 转换秒为时间
- 最大公约数
- 杨辉三角
- 线性查找
- 七段数码管绘制
- 斐波那契数列计算
- 汉诺塔实践
- 合法的用户名
- 科赫雪花小包裹
- 密码的强度
- 藏头诗
- 统计字符出现次数
- 文件扩展名
- 插入排序
- 选择排序
- 冒泡排序
- 二分查找
打招呼函数
请用程序实现
用函数给某个人打招呼。
函数定义
def say_hello (name):
pass
参数说明
name是一个字符串,表示名字。
返回值说明
该函数没有返回值,调用该函数会输出一段话:你好,xxx,认识你很高兴!
示例 1
| 参数 | 输出 |
|---|---|
| name = "张三" | 你好,张三,认识你很高兴! |
示例 2
| 参数 | 输出 |
|---|---|
| name = "李四" | 你好,李四,认识你很高兴! |
"""
练习:打招呼函数
要求:
1. 定义函数 say_hello
2. 有 1 个参数 name 表示要给谁打招呼
3. 实现函数功能,即在控制台打印:`你好,,认识你很高兴!`(注:name 是函数的参数)
"""
def say_hello (name):
return print("你好,"+name+",认识你很高兴!")
name = input()
say_hello (name)
能否组成三角形
判断三条线段能否构成一个三角形,需要满足两条规则:
三角形的三条边长必须大于零。
任意两边之和必须大于第三边。
请用程序实现
用函数判断三个数字能否构成三角形,并将判断结果返回。
函数定义
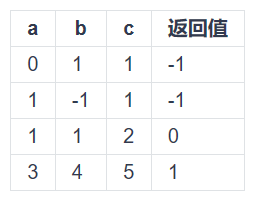
def is_triangle (a, b, c):
pass
参数说明
a, b, c均为整数。
返回值说明
- 三角形三边长必须大于零,不满足则返回数字-1,表示数据不合法;
- 任意两边之和必须大于第三边:
·不满足则返回数字0,表示不能组成三角形;
·满足则返回数字1,表示能组成三角形。
"""
编写 is_triangle 函数,此函数有 3 个参数,分别为3个数字,
判断这3个数字所代表的边长能否组成一个三角形
"""
"""请实现函数"""
"""
编写 is_triangle 函数,此函数有 3 个参数,分别为3个数字,
判断这3个数字所代表的边长能否组成一个三角形
"""
def is_triangle(a, b, c):
if a<=0 or b<=0 or c<=0:
return -1
if a+b>c and a+c>b and b+c>a and a-b<c and a-c<b and b-c<a:
return 1
else:
return 0
a=3
b=4
c=5
print(is_triangle(a,b,c))
计算n个自然数的立方和
定义一个函数,其功能是计算 n 个自然数的立方和,如下图所示。请编写函数完成要求。
![]()
1. 定义函数 sumOfSeries
2. 有 1 个参数 n 表示自然数的个数
3. 有 1 个返回值,返回自然数的立方和
4. 调用函数,使函数执行后在控制台打印:'和为:xx’
请在右侧编辑器中编写代码,完成练习。
# 定义立方和的函数
def sumOfSeries(n):
s=0
for i in range(1,n+1):
s += i**3
return str(s)
# 调用函数
print("和为:",sumOfSeries(5))
简单计算器实现
请用程序实现
用函数实现 加、减、乘、除 的运算。
函数定义
# 加法函数
def addition (num1, num2):
pass
# 减法函数
def subtraction (num1, num2):
pass
# 乘法函数
def multiplication (num1, num2):
pass
# 除法函数
def division (num1, num2):
pass
参数说明
num1,num2均为整数,表示需要进行计算的两个数字。
返回值说明
四个函数的返回值,均为执行对应操作后计算出来的值。
这里使用加法函数做演示:
示例 1
| 参数 | 返回 |
|---|---|
| num1 = 3 num2 = 4 |
7 |
示例 2
| 参数 | 返回 |
|---|---|
| num1 = 9 num2 = 1 |
10 |
# 定义加法函数 addition
def addition (num1, num2):
return num1+num2
# 定义减法函数 subtraction
def subtraction (num1, num2):
return num1-num2
# 定义乘法函数 multiplication
def multiplication (num1, num2):
return num1*num2
# 定义除法函数 division
def division (num1, num2):
return num1/num2
num1 = 4
num2 = 5
print(multiplication(num1,num2))
转换秒为时间
1 天有 86400 秒,那么 100000 秒相当于多长时间呢?
请用程序实现
用函数实现,将一个指定的秒数转换为[天, 时, 分, 秒]的数据格式,并将其返回。
函数定义
def convert_from_seconds (seconds):
pass
参数说明
seconds是一个整数,表示待转换的秒数。
返回值说明
函数返回一个列表,列表内存储的值分别为
[天, 时, 分, 秒],且0 ≤ 秒 ≤ 59,0 ≤ 分 ≤ 59,0 ≤ 时 ≤ 23,天 ≥ 0。
示例 1
| 参数 | 返回 |
|---|---|
| seconds = 610 | [0, 0, 10, 10] |
示例 2
| 参数 | 返回 |
|---|---|
| seconds = 100000 | [1, 3, 46, 40] |
# 定义一个 convert_from_seconds 函数, 参数 seconds, 返回表示时间的列表
def convert_from_seconds(seconds):
a=seconds//86400
b=seconds%86400//3600
c=seconds%3600//60
d=seconds%60
list=[]
list.append(a)
list.append(b)
list.append(c)
list.append(d)
return list
seconds = 100000
print(convert_from_seconds(seconds))
最大公约数
请用程序实现
用函数计算两个整数的最大公约数,并将计算结果返回。
函数定义
def common_divisor (num1, num2):
pass
参数说明
num1, num2均为正整数。
返回值说明
返回值为整数,且为num1和num2的最大公约数。
示例 1
| 参数 | 返回 |
|---|---|
| num1 = 24 num2 = 16 |
8 |
示例 2
| 参数 | 返回 |
|---|---|
| num1 = 25 num2 = 15 |
5 |
# 定义并实现函数 common_divisor
def common_divisor (num1, num2):
n=min(num1,num2)
for i in range(1,n+1):
if ((num1%i==0) and (num2%i==0)):
res=i
return res
# 调用函数
result = common_divisor(24, 16)
print(result)
杨辉三角
杨辉三角,又称贾宪三角形、帕斯卡三角形,是二项式系数在三角形中的一种几何排列。以下是杨辉三角的前十行:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
1 9 36 84 126 126 84 36 9 1
由上可以看出:
每行端点与结尾的数为 1
每个数等于它上方两数之和
每行数字左右对称,且由 1 开始逐渐变大
第 n 行的数字有 n 项
请用程序实现
用函数实现,返回一个指定行数的杨辉三角数列。
函数定义
def pascal_triangle (num):
pass
参数说明
num是一个整数,表示需要输出的行数。
返回值说明
函数返回一个列表,列表内存储的值为杨辉三角某一行的数据。
示例 1
| 参数 | 返回 |
|---|---|
| 3 | [1, 2, 1] |
示例 2
| 参数 | 返回 |
|---|---|
| 6 | [1, 5, 10, 10, 5, 1] |
# 定义函数 pascal_triangle 接受参数 num,并返回杨辉三角第 num 行
def pascal_triangle(num):
# j行的数据, 应该由j - 1行的数据计算出来.
# 假设j - 1行为[1,3,3,1], 那么我们前面插入一个0(j行的数据会比j-1行多一个),
# 然后执行相加[0+1,1+3,3+3,3+1,1] = [1,4,6,4,1], 最后一个1保留即可.
r=[1]
for i in range(1,num):
r.insert(0,0)
# 因为i行的数据长度为i+1, 所以j+1不会越界, 并且最后一个1不会被修改.
for j in range(i):
r[j]=r[j]+r[j+1]
return r
print(pascal_triangle(3))
线性查找
线性查找指按一定的顺序检查列表中每一个元素,直到找到所要寻找的特定值为止示。
定义一个函数,其功能是线性查找列表中的元素,如下图所示。请编写函数完成要求。
请用程序实现:定义线性查找函数 linear_searching,接受三个参数 要进行查找的列表(list)、列表长度(size)、目标元素(target),在 list 中查找 target,如果 target 在 list 中则将 target 的索引返回;否则返回数字 -1。
# 定义函数 linear_searching 接受参数 list, size, target,并将查找结果返回
def linear_searching(list, size, target):
for i in range(size):
if list[i] ==target:
return i
return -1
list=['a','b','w','q','g']
size=len(list)
target='b'
print(linear_searching(list, size, target))
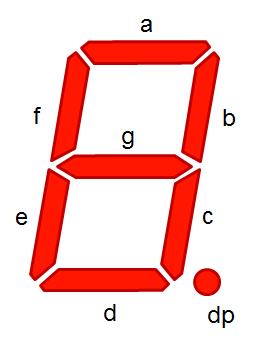
七段数码管绘制
七段数码管是一种展示数字的有效方式。
请用程序绘制当前系统时间对应的七段数码管,效果如下:
要求如下:
(1) 使用 time 库获得系统当前时间,格式如下:20190411
(2) 绘制对应的七段数码管
(3) 数码管风格不限
#七段数码管的绘制
import turtle as t
import time
def drawgap():
t.pu()
t.fd(5)
def drawline(draw):#绘制单段数码管
t.pendown() if draw else t.penup()
t.fd(40)
drawgap()
t.right(90)
def drawdigit(digit):#根据数值绘制七段数码管
drawline(True) if digit in [2,3,4,5,6,8,9] else drawline(False)
drawline(True) if digit in [0,1,3,4,5,6,7,8,9] else drawline(False)
drawline(True) if digit in [0,2,3,5,6,8,9] else drawline(False)
drawline(True) if digit in [0,2,6,8] else drawline(False)
t.left(90)
drawline(True) if digit in [0,4,5,6,8,9] else drawline(False)
drawline(True) if digit in [0,2,3,5,6,7,8,9] else drawline(False)
drawline(True) if digit in [0,1,2,3,4,7,8,9] else drawline(False)
t.left(180)
t.pu()#为绘制后续数字确定位置
t.fd(20)#为绘制后续数字确定位置
def drawdate(date):#获取日期
t.pencolor("green")
for i in date:
if i == '年':
t.write('年',font = ("Arial",18,"normal"))
t.pencolor("blue")
t.fd(40)
elif i == "月":
t.write('月',font = ("Arial",18,"normal"))
t.pencolor("yellow")
t.fd(40)
elif i == "日":
t.write('日',font = ("Arial",18,"normal"))
t.pencolor("red")
else:
drawdigit(eval(i))#通过eval()将数字变成整数
def main(date):
t.setup(1500,650,20,20)
t.pu()
t.fd(-600)
t.pensize(5)
drawdate(time.strftime("%Y年%m月%d日",time.gmtime()))
t.fd(40)
t.color("red")
drawdate(date)
t.hideturtle()
t.done()
main(input("请输入一个年月日,例:2019年01月22日:\n"))
斐波那契数列计算
形如1,1,2,3,5,8…的数列,被称之为斐波那契数列。这个数列的特点是从第三个数字开始,每个数字都等于前两个数字之和。
请用程序实现
用函数实现,计算斐波那契数列某项的值,并将计算结果返回。
函数定义
def fbi (num):
pass
参数说明
num是一个整数,表示斐波那契数列的项数。
返回值说明
函数返回一个整数,该整数为斐波那契数列第 num 项的值。
示例 1
| 参数 | 返回 |
|---|---|
| 4 | 3 |
示例 2
| 参数 | 返回 |
|---|---|
| 6 | 8 |
# 定义一个 fbi 函数,参数 num,返回斐波那契数列第 num 项的值。
def fbi (num):
if num == 1 or num == 2:
return 1
else:
return fbi (num-1) +fbi (num-2)
num = eval(input())
print(fbi(num))
汉诺塔实践
请用程序实现
用函数实现汉诺塔的移动步骤拆解。
函数定义
def hanoi (n, src, dst, mid):
pass
参数说明
n是整数,表示圆柱A上面的圆盘个数。
src是大写字母A,表示最左边的圆柱。
dst是大写字母C,表示最右边的圆柱。
mid是大写字母B,表示中间的圆柱。
返回值说明
此函数没有返回值,调用函数后函数输出圆盘移动的步骤。
# 请在...补充一行或多行代码
count = 0
def hanoi (n, src, dst, mid):
global count
if n == 1:
print("{}: {}->{}".format(1, src, dst))
count += 1
else:
#先把最上面的所有盘src->mid,移动过程用到dst
hanoi(n-1,src,mid,dst)
#把最下面的盘src->dst
print("{}: {}->{}".format(n, src, dst))
# print(f"第{n}个盘从{src}-->{dst}")
#把mid塔的所有盘从mid-->dst,移动过程使用到a
hanoi(n-1,mid,dst,src)
hanoi(3, "A", "C", "B")
print(count)
合法的用户名
有一些网站注册用户时,会对用户名长度进行限制,比如用户名的长度必须在6(含)~18(含)位之间。
请用程序实现
用函数实现对用户名的合法性进行检查。
函数定义
def check_username (username):
pass
参数说明
username是一个任意长度的字符串,表示待检查的用户名。
返回值说明
如果用户名长度在
6(含)~18(含),则用户名有效,返回True;否则返回False。
示例 1
| 参数 | 返回 |
|---|---|
| username = ‘zhangsan’ | True |
示例 2
| 参数 | 返回 |
|---|---|
| username = ‘lisi’ | False |
"""
实现 check_username 函数,检查 username 是否有效
username 长度在 6-18 位之间,返回 True,否则返回 False
"""
def check_username(username):
if 6 <= len(username) <= 18:
return True
else:
return False
username = input()
print(check_username(username))
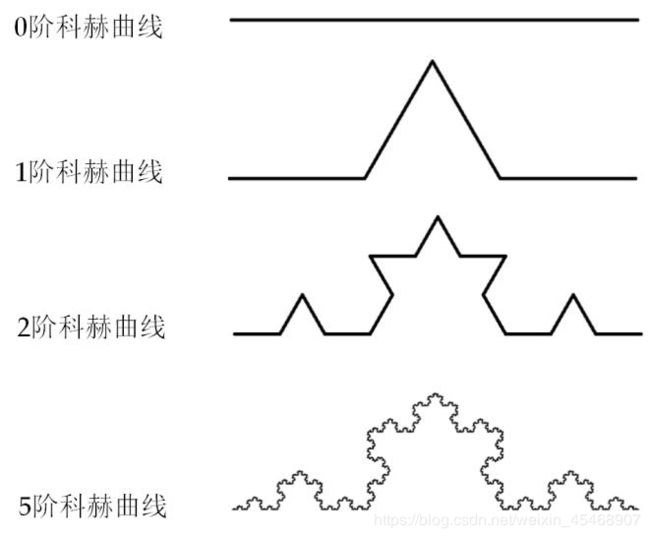
科赫雪花小包裹
请补充编程模板中代码,完成功能:获得用户输入的整数level,作为阶,绘制level阶科赫曲线。
# 请在...补充一行或多行代码
import turtle
def koch(size, n):
if n==0:
turtle.fd(size)
else:
for angle in [0,60,-120,60]:
turtle.left(angle)
koch(size/3,n-1)
def main(level):
turtle.setup(600,600)
turtle.penup()
turtle.goto(-200, 100)
turtle.pendown()
turtle.pensize(2)
koch(400,level)
turtle.right(120)
koch(400,level)
turtle.right(120)
koch(400,level)
turtle.hideturtle()
try:
level = eval(input("请输入科赫曲线的阶: "))
main(level)
except:
print("输入错误")
密码的强度
密码是账户的重要安全保障,涉及到安全问题,太简单的密码容易被猜到或破解。
请用程序实现
用函数实现一个校验密码强度的函数,用于提醒用户在注册时,密码是否足够安全。
以下为密码强度校验规则:
密码长度在 6 位及以上,强度
+1,在 8 位及以上,强度+2,12位及以上,强度+4
有大写字母,强度+2
除字母外,还包含数字,强度+2
有除字母、数字以外字符强度+2
函数定义
def passworld_strength (pwd):
pass
参数说明
pwd是一个字符串,表示需要检查的密码。
返回值说明
函数返回一个整数,表示密码强度。
示例 1
| 参数 | 返回 |
|---|---|
| pwd = ‘aA23’ | 4 |
示例 2
| 参数 | 返回 |
|---|---|
| pwd = ‘aA_345678912’ | 10 |
"""
实现密码强度计算函数:
1. 实现函数 passworld_strength 返回 0-10 的数值,表示强度,数值越高,密码强度越强
2. 密码长度在 6 位及以上,强度 +1,
在 8 位及以上,强度 +2,
在 12 位及以上,强度 +4
3. 有大写字母,强度 +2
4. 除字母外,还包含数字,强度 +2
5. 有除字母、数字以外字符,强度 +2
"""
def password_strength(pwd):
intensity=0
if len(pwd)>=12:
intensity+=4
elif 8<=len(pwd)<12:
intensity+=2
elif 6<=len(pwd)<8:
intensity+=1
pwdlist=list(pwd)
for i in range(len(pwd)):
if 'A'<=pwdlist[i]<='Z':
intensity+=2
break
for i in range(len(pwd)):
if 'A'<=pwdlist[i]<='Z' or 'a'<=pwdlist[i]<='z':
for j in range(len(pwd)):
if '0'<=pwdlist[j]<='9':
intensity+=2
break
break
for i in range(len(pwd)):
if ('null'<=pwdlist[i]<'0') or ('9'<pwdlist[i]<='@') or ('Z'<pwdlist[i]<='`') or ('z'<pwdlist[i]<='~'):
intensity+=2
break
return intensity
pwd1=str(input())
print(password_strength(pwd1))
藏头诗
古人经常使用藏头诗,隐晦的表达自己的想说的话,既有诗意,又能传递信息,比如下面这两首诗:
芦花丛中一扁舟,
俊杰俄从此地游。
义士若能知此理,
反躬难逃可无忧。
我画蓝江水,
爱晚亭上枫。
秋月溶溶照,
香烟袅袅绕。
请用程序实现
用函数实现,将藏头诗中隐含的意思找出来。
函数定义
def acrostic (poem):
pass
参数说明
poem是一个列表,其保存了一首诗。
返回值说明
函数返回一个字符串,字符串为藏头诗中隐含的意思。
示例 1
| 参数 | 返回 |
|---|---|
| poem = [“芦花丛中一扁舟”, “俊杰俄从此地游”, “义士若能知此理”, “反躬难逃可无忧”] |
芦俊义反 |
示例 2
| 参数 | 返回 |
|---|---|
| poem = [“我画蓝江水”, “爱晚亭上枫”, “秋月溶溶照”, “香烟袅袅绕”] |
我爱秋香 |
poem1 = [
"芦花丛中一扁舟",
"俊杰俄从此地游",
"义士若能知此理",
"反躬难逃可无忧"
]
poem2 = [
"我画蓝江水",
"爱晚亭上枫",
"秋月溶溶照",
"香烟袅袅绕"
]
def acrostic(poem):
newstr=[]
for i in range(len(poem)):
str1=poem[i]
rstr=list(str1)
newstr.append(rstr[0])
str1=""
newstr1=''.join(newstr)
return newstr1
print(acrostic(poem1))
print(acrostic(poem2))
统计字符出现次数
请用程序实现
用函数实现,统计字符串中指定字符出现的次数。
注意: 禁止使用count()函数。
函数定义
def sum_char (string, char):
pass
参数说明
string是一个字符串,char是一个字符
返回值说明
函数返回一个整数,表示字符 char 在 string 中出现的次数。
示例 1
| 参数 | 返回 |
|---|---|
| string = 'hello,world’ char = 'l’ |
3 |
示例 2
| 参数 | 返回 |
|---|---|
| string = ‘hello,world’ char = 'o’ |
2 |
"""
统计字符串 string 中出现字符 char 的次数,并返回;
char 是长度为 1 的字符串。
"""
def sum_char(string, char):
n=0
for i in range(len(string)):
if string[i] == char:
n+=1
return n
string=input()
char=input()
print(sum_char(string, char))
文件扩展名
文件扩展名是操作系统用来标记文件类型的一种机制。通常来说,一个扩展名是跟在主文件名后面的,由一个分隔符(.)分隔。
请用程序实现
用函数实现,将文件的扩展名获取出来。
函数定义
def file_ext (filename):
pass
参数说明
filename是一个字符串,表示文件名。
返回值说明
如果 filename 有扩展名,则函数返回该 filename 的扩展名,否则返回
文件名错误。
示例 1
| 参数 | 返回 |
|---|---|
| filename = “logo.png” | png |
示例 2
| 参数 | 返回 |
|---|---|
| filename = “main.py” | py |
"""
获取文件扩展名
说明:实现 file_ext 函数,该函数接受一个表示文件名的字符串参数 filename,返回它的扩展名
"""
def file_ext(filename):
for i in range(len(filename)):
if filename[i] == '.':
return filename[i+1:]
filename = input()
print(file_ext(filename))
插入排序
插入排序(英语:Insertion Sort)是一种简单直观的排序算法。
它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
定义一个函数,其功能是进行插入排序,如下图所示。请编写函数完成要求。
请用程序实现:定义插入排序函数 insertion_sort 接受参数 list_sort,在函数内部对 list_sort 进行插入排序,并将排序后的列表返回。
# 定义函数 insertion_sort 接受参数 list_sort,并返回插入排序结果。
def insertion_sort(list_sort):
n = len(list_sort)
for j in range(n):
i = j
while i > 0:#和有序表中的每个一样元素进行比较(从最后一个开始)
if list_sort[i] < list_sort[i-1]:
list_sort[i],list_sort[i-1] = list_sort[i-1],list_sort[i]
i -= 1
else:
break
return list_sort
list_sort = [9,8,8,7,6,5,4,3,2,1]
print(insertion_sort(list_sort))
选择排序
选择排序(Selection sort)是一种简单直观的排序算法。
它的工作原理如下。首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置,
然后,再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。以此类推,直到所有元素均排序完毕。
定义一个函数,其功能是进行选择排序,如下图所示。请编写函数完成要求。
选择排序
请用程序实现: 定义选择排序函数 selection_sort 接受参数 list_sort,在函数内部对 list_sort 进行选择排序,并将排序后的列表返回。
# 定义函数 selection_sort 接受参数 list_sort,并返回选择排序结果。
def selection_sort(list_sort):
for i in range(len(list_sort)):
for j in range(i, len(list_sort)):
if list_sort[i] > list_sort[j]:
list_sort[i], list_sort[j] = list_sort[j], list_sort[i]
return list_sort
list_sort = [9, 8, 7, 6, 5, 4, 3, 2, 1]
print(selection_sort(list_sort))
冒泡排序
冒泡排序(Bubble Sort)也是一种简单直观的排序算法。
它重复地走访过要排序的数列,一次比较两个元素,如果他们的顺序错误就把他们交换过来。
走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢"浮"到数列的顶端。
定义一个函数,其功能是进行冒泡排序,如下图所示。请编写函数完成要求。
请用程序实现: 定义冒泡排序函数 bubble_sort 接受参数 list_sort,在函数内部对 list_sort 进行冒泡排序,并将排序后的列表返回。
# 定义函数 bubble_sort 接受参数 list_sort,并返回冒泡排序结果
def bubble_sort(list_sort):
n = len(list_sort)
for i in range(n):
for j in range(0, n-i-1):
if list_sort[j] > list_sort[j+1] :
list_sort[j], list_sort[j+1] = list_sort[j+1], list_sort[j]
return list_sort
list_sort = [9, 8, 7, 6, 5, 4, 3, 2, 1]
print (bubble_sort(list_sort))
二分查找
二分搜索是一种在有序数组中查找某一特定元素的搜索算法。
搜索过程从数组的中间元素开始,如果中间元素正好是要查找的元素,则搜索过程结束;
如果某一特定元素大于或者小于中间元素,则在数组大于或小于中间元素的那一半中查找,而且跟开始一样从中间元素开始比较。如果在某一步骤数组为空,则代表找不到。
这种搜索算法每一次比较都使搜索范围缩小一半。
定义一个函数,其功能是进行二分查找,如下图所示。请编写函数完成要求。
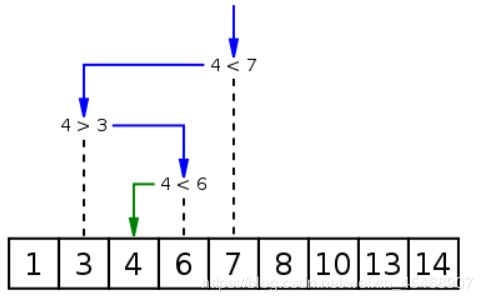
请用程序实现: 定义二分查找函数 binary_search 接受参数 要进行查找的列表(list_sort)、列表长度(size)、目标元素(target)。在函数内部检查 target 是否在 list_sort 中,如果在则返回 target 的索引;如果不在则返回数字 -1。
# 定义函数 binary_search 接受参数 list_sort, size, targer,并将查找结果返回
def binary_search(list_sort, size, targer):
low = 0
high = size - 1
while low <= high:
mid = int((low + high) / 2)
guess = list_sort[mid]
if guess == targer:
return mid
if guess > targer:
high = mid - 1
else:
low = mid + 1
return -1
list_sort = [1,2,3,4,5,6,7,8,9,10]
targer = 3
print(binary_search(list_sort, len(list_sort), targer))